86. 5. Поняття функції (відображення)

Означення 1.18. Нехай та – деякі множини. Кажуть, що функція, визначена на із значеннями в , якщо за певним законом кожному елементу відповідає елемент . Множину називають областю визначення функції. Множину всіх значень функції, які вона приймає на елементах множини називають множиною значень або областю значень функції.

Для функції (відображення) прийняті наступні позначення: ,

Зауважимо, що термін „функція” вперше з’явився в 1692р. у Г. Лейбніца (G.W. Leibnitz), але в більш вузькому розумінні. В сучасному розумінні цей термін вжив Й. Бернуллі (J. Bernoulli) в листі до Лейбніца в 1698 році.

Означення 1.19. Відображення називають взаємно-однозначним, якщо рівняння для кожного має не більше одного розв’язку.

Означення 1.20. Відображення називають сюр’єктивним, якщо для кожного має не менше одного розв’язку.

Означення 1.21. Відображення називають бієктивним, якщо рівняння для кожного має єдиний розв’язок.

87. 6. Еквівалентні множини. Потужність множин

Означення 1.22. Множини і називають еквівалентними, якщо за певним законом можна встановити взаємно-однозначну відповідність елементів. Еквівалентні множини позначають: ~ .

Множина рівнопотужна множині , якщо існує бієктивне відображення на . Відношення рівнопотужності є відношенням еквівалентності і розбиває сукупність всіх множин на класи еквівалентних між собою. Множини одного класу еквівалентності мають однакову кількість елементів, різних – різну.

Означення 1.23. Клас еквівалентних множин, якому належить множина , називають потужністю множини , або кардиналом чи кардинальним числом, позначається або . Якщо ~ , то пишуть, що .

Кажуть, що , якщо рівнопотужна деякій підмножині множини . Множина може бути рівнопотужна своїй підмножині. Можливість для множини бути рівнопотужною своїй частині є характерною ознакою нескінченних множин, яку Дедекінд (R. Dedekind) запропонував вважати означенням нескінченної множини. Множина називається скінченною (по Дедекінду), якщо вона не рівнопотужна ніякій своїй підмножині. В іншому випадку вона нескінченна.

Наведемо основні властивості потужностей:

1) ;

2) – теорема Шредера-Бернштейна (F. Schröder);

3) – теорема Кантора.

Розглянемо множину всіх підмножин множини : . Тоді справедлива теорема Кантора: . Також можна стверджувати, що .

Останнє твердження показує, що якщо нескінченні множини існують, то і „нескінченності” бувають різні.

Потужність скінченної множини дорівнює кількості її елементів. Нескінченні множини, еквівалентні множині , називаються зчисленними множинами, а їх потужність називають зчисленною потужністю і позначають .

Наведемо основні властивості зчисленних множин.

1. Будь-яка нескінченна підмножина зчисленної множини є зчисленною множиною.

2. Якщо від зчисленної множини відкинути скінченну множину елементів, то потужність нескінченної множини, яка залишилась, буде .

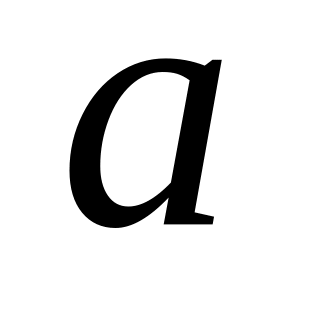3. Зчисленна множина зчисленних множин є зчисленною множиною.

4. Об’єднання скінченної кількості зчисленних множин є зчисленною множиною.

Множина ~ , тобто . Множина ~ , тобто .