145. 12. Економічні задачі

Нехай задана виробнича функція , що виражає залежність, наприклад, витрат виробництва від кількості двох видів продукції і , що виготовляються. Припустимо, що чинник змінився на , тоді виробнича функція зміниться на .

Вираз відображає середній приріст виробничої функції на одиницю приросту чинника , чи середні витрати виробництва на одиницю продукції . Перейшовши до границі при , одержимо граничні витрати виробництва на одиницю продукції : . Аналогічно за чинником : .

Еластичність виробничої функції щодо чинників виробництва і встановлюється так: і вказує приблизно процентний приріст виробничої функції (підвищення, зниження), що відповідає приросту чинника на 1% за умови, якщо чинник не змінюється; і вказує приблизно відсотковий приріст виробничої функції, що відповідає приросту чинника на 1% за умови, якщо чинник не змінюється.

Якщо виробнича функція встановлює залежність випуску від виробничих чинників , , ..., у вигляді , то диференціальними характеристиками такої функції є: – гранична ефективність відносно чинника , – еластичність випуску відносно та інші.

Приклад 4.10. Для випуску деякого товару визначена виробнича функція , де , – чинники виробництва. Визначити: а) закон зміни виробничої функції; б) еластичність функції за кожним чинником; в) коефіцієнт еластичності за чинниками при , .

Розв’язання. Для визначення зміни виробничої функції за чинниками і відповідно, необхідно знайти і :

; .

За означенням еластичність функції за кожним з чинників така:

; .

Обчислимо коефіцієнти еластичності при , . Врахуємо, що :

, .

Таким чином, зі збільшенням чинника на 1% відбудеться відносне збільшення заданої виробничої функції приблизно на 0,89% (за умови стабільності чинника ).

При збільшенні чинника на 1% і незмінності чинника виробнича функція збільшиться приблизно на 0,26%. Виходить, найбільший вплив на виробничу функцію робить чинник .

Відзначимо, що від'ємне значення коефіцієнта еластичності показує зменшення виробничої функції при збільшенні відповідного чинника. Наприклад, якщо і – функція випуску продукції, то збільшення чинника на 1% приводить до зниження випуску продукції на 0,08%.

Приклад 4.11. Фірма реалізує частину товару на внутрішньому ринку, а іншу частину поставляє на експорт. Зв'язок ціни товару і його кількості , проданого на внутрішньому ринку, описується рівнянням кривої попиту: . Аналогічно для експорту ціна і кількість також зв'язані відношенням (рівнянням кривої попиту): . Сумарні витрати визначаються виразом: . Яку цінову політику повинна проводити фірма, щоб прибуток був максимальний?

Розв’язання. Сумарний доход: , де , – доходи від продажу на внутрішньому ринку і від експортних постачань відповідно:

, .

В обох випадках ціна береться з відповідних кривих попиту.

.

Одержуваний фірмою прибуток

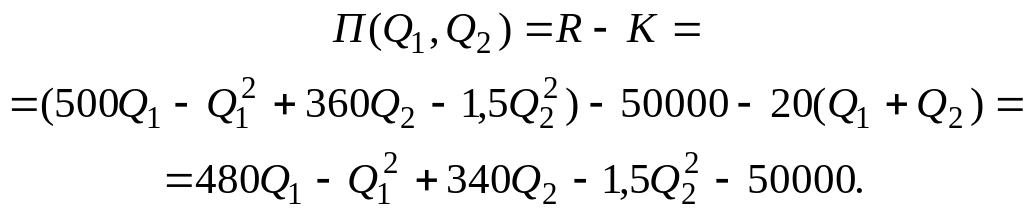
Знаходимо частинні похідні першого порядку:

, ,

Стаціонарна точка .

Обчислюємо частинні похідні другого порядку:

, , ,

, .

Виходить, у стаціонарній точці існує максимум.

Знайдемо оптимальні ціни для продажу на внутрішньому і зовнішньому ринках, підставляючи координати точки максимуму в криві попиту: ,

.

Підраховуємо максимальний прибуток при оптимальних об'ємах продажу на внутрішньому і зовнішньому ринках:

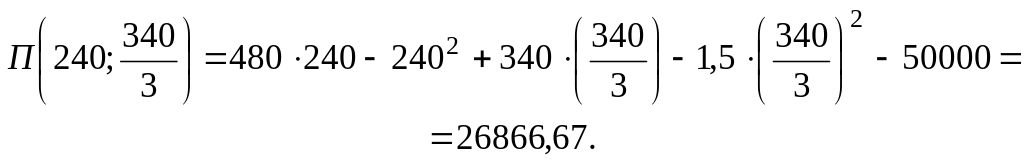
Приклад 4.12. Фірма робить два види товарів і і продає їх за ціною 1000 грош. од. і 800 грош. од. відповідно. Об'єми випуску товарів – і . Функція витрат має вигляд

.

Потрібно знайти такі значення і , при яких прибуток, одержуваний фірмою, максимальний і знайти цей прибуток.

Розв’язання. Сумарний доход від продажу товарів і :

.

Прибуток являє собою різницю між доходом і витратами , тому ,

.

Це і є функція, максимум якої потрібно знайти. Для знаходження стаціонарних точок, визначаємо частинні похідні першого порядку від функції і прирівнюємо їх до нуля:

, ,

Стаціонарна точка . Знаходимо частинні похідні другого порядку:

, , ,

, .

Таким чином, точка є точкою максимуму. Максимальний прибуток досягається при об'ємах виробництва , . Знайдемо суму максимального прибутку:

Вправи

4.1. Знайти область визначення функції і побудувати її на площині:

а) ; б) ; в) .

4.2. На площині побудувати сімейство ліній рівня:

а) ; б) .

4.3–4.12. Знайти частинні похідні першого порядку.

4.3. . 4.4. .

4.5. . 4.6. .

4.7. . 4.8. .

4.9. . 4.10. .

4.11. . 4.12. .

4.13. Знайти повні диференціали функцій:

а) ; б) ; в) ;

г) ; д) .

4.14. Обчислити приблизно за допомогою повного диференціала:

а) ; б) ; в) .

4.15. Знайти похідну функцію в напрямку прямої у точці .

4.16. Знайти градієнт функції в точці .

4.17. Знайти напрямок найбільшої зміни функції в точці .

4.18. Знайти похідні другого порядку функцій:

а) ; б) ; в) ;

г) ; д) .

4.19. Дослідити функції на екстремум:

а) ; б) ;

в) ; г) ;

д) .

4.20. Наводяться дані про ріст продуктивності праці і зниження собівартості продукції по підприємству за 5 років стосовно базисного періоду, прийнятому за одиницю:

Час у роках	1	2	3	4	5
Продуктивність праці	1,05	1,09	1,13	1,18	1,24
Собівартість продукції	0,98	0,95	0,93	0,90	0,88

Лінійна залежність зниження собівартості від росту продуктивності праці . По цим даним знайти параметри і , застосувавши спосіб найменших квадратів.

4.21. Нехай – виробнича функція. Знайти закон зміни виробничої функції за кожним з чинників, і , коефіцієнти еластичності по витратах точці . Зробити висновки:

а) ;

б) ;

г) ;

д) ;

є) ;

ж) .

4.22. Потік пасажирів виражається функцією , де – число мешканців; – відстань між містами. Знайти частинні похідні і пояснити їх зміст.

4.23. Фірма виробляє два види товарів в кількостях і відповідно. Функція витрат має вигляд , а крива попиту для кожного товару , , де , – ціна одиниці товару. Крім цього, фірма пов’язана обмеженням на загальний об’єм виробництва товарів, її квота складає 15 одиниць, тобто . Знайти максимальний прибуток, який може бути досягнутий за цією умовою.

4.24. Є такі дані про ціну на нафту , грош. од. та індекс акцій нафтових компаній , умов. од.:

	17,28	17,05	18,30	18,80	19,20	18,50
	537	534	550	555	560	552

Припускаючи, що між змінними і існує лінійна залежність , знайти і використовуючи метод найменших квадратів.

4.25. Фірма виробляє два види товарів та і продає їх за ціною 500 грош. од. та 800 грош. од. відповідно. Обсяги випуску товарів – та . Функція витрат має вигляд . Знайти такі значення та за яких прибуток, отриманий фірмою, максимальний. Обчислити цей прибуток.

4.26. Сумарний прибуток підприємства залежить від виду двох ресурсів та і виражається функцією . Визначити витрати ресурсів та , що забезпечують максимальний прибуток підприємства і знайти його для функцій:

а) ;

б) ;

в) ;

г) .

4.27. Річні видатки підприємства можуть бути виражені функцією . При яких та видатки підприємства будуть найменшими? Розрахувати коефіцієнти еластичності при .

4.28. Фірма вирішила щомісяця вкладати 10000 грош. од. на виробництво деякої продукції. Нехай середня заробітна платня по фірмі складає 200 грош. од., а вартість одиниці сировини дорівнює 100 грош. од. Визначити яку кількість робочих потрібно та яка кількість сировини необхідно придбати фірмі для одержання найбільшого об’єму продукції , якщо відомо, що об’єм прямо пропорційний до кількості робочих та кількості сировини з коефіцієнтом пропорційності рівним 10.

4.29. Функція корисності має вигляд . Ціна одиниці першого блага дорівнює 9, другого – 18. На придбання цих благ може бути затрачена сума, рівна 800. Як потрібно розподілити цю суму між двома благами, щоб користь від цих придбань була найбільшою.

4.30. Функція витрат , а також функція кількості реалізованого товару при встановленій ціні за одиницю, рівній . Знайти оптимальні значення та для монополіста-виробника у двох випадках:

а) , ;

б) , .