Друга достатня умова екстремуму.

Нехай функція визначена і двічі диференційована в точці і її околі і при цьому . Тоді, якщо , функція в точці має мінімум, якщо ж , функція в точці має максимум.

Доведемо це твердження, використовуючи означення другої похідної:

( за умовою).

Нехай , тоді . При (ліворуч від точки ) різниця , з чого випливає, що . При (праворуч від точки x₀) різниця , отже . Як бачимо, при переході через точку перша похідна змінює знак з від'ємного на додатний, значить у точці функція має мінімум.

Аналогічно можна показати, що якщо , то функція має в точці максимум.

Дана достатня умова дозволяє швидко знаходити гладкі екстремуми функції, якщо обчислення проміжків монотонності необов'язкове. Особливо ця умова полегшує дослідження екстремальних значень у прикладних задачах.

Третя достатня умова екстремуму.

Нехай і непарне число, функція визначена і разів диференційована в околі точки . Тоді, якщо

,

то, функція в точці має мінімум при , максимум при .

129. 21. Найбільше і найменше значення функції на відрізку

Нехай функція неперервна на відрізку . Тоді на цьому відрізку функція набуває найбільшого і найменшого значень. Будемо припускати, що на даному відрізку функція має скінченну кількість критичних точок. Якщо найбільшого значення функція набуває всередині відрізка , то очевидно, що це значення буде одним з максимумів функції, якщо їх декілька – найбільшим максимумом. Найбільшого значення функція може набувати і на одному з кінців відрізка.

Те саме можна сказати і про найменше значення функції: воно досягається або на одному з кінців відрізка, або в деякій внутрішній точці відрізка, що є точкою мінімуму.

Звідси випливає алгоритм обчислення найбільшого і найменшого значень функції на відрізку .

1. Перевірити, чи належить відрізок області визначення функції.

2. Знайти всі критичні точки функції і вибрати ті з них, що належать відрізку .

3. Обчислити значення функції в обраних критичних точках і на кінцях відрізку.

4. З усіх отриманих значень функцій вибрати найбільше і найменше.

Приклад 3.21. Знайти найбільше і найменше значення функції на відрізку .

Розв’язання. Дана функція визначена для будь-якого дійсного . Її похідна

.

Критичні точки визначимо, розв’язавши рівняння . Корені цього рівняння , , . Перший корінь не належить заданому відрізку, тому обчислимо значення функції в точках , і на кінцях відрізка. Одержимо

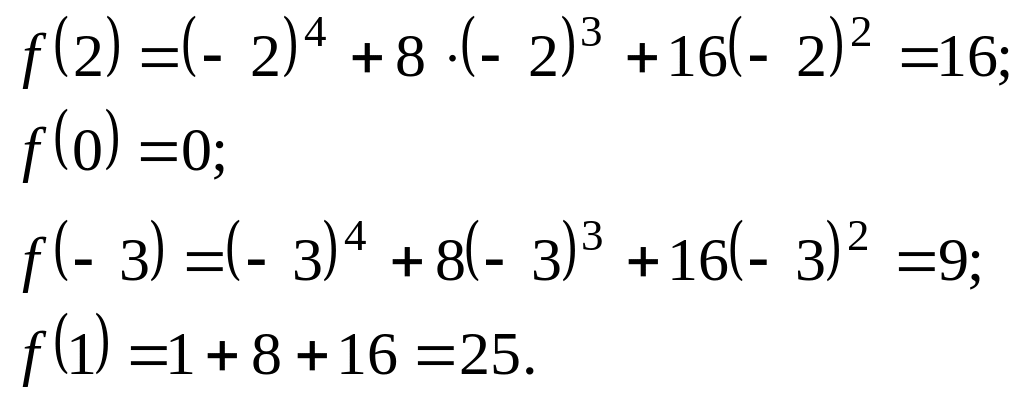
Порівнюючи ці значення, бачимо, що найменше значення функції , а найбільше значення функції .

130. 22. Випуклість, увігнутість графіка функції. Перегин

Нехай функція визначена в точці і двічі диференційована в її околі.

Означення 3.6. Графік функції називається випуклим у точці , якщо в деякому околі цієї точки графік розташований нижче дотичної, проведеної в точці , і увігнутим, якщо графік розташований вище дотичної.

Рис. 3.15.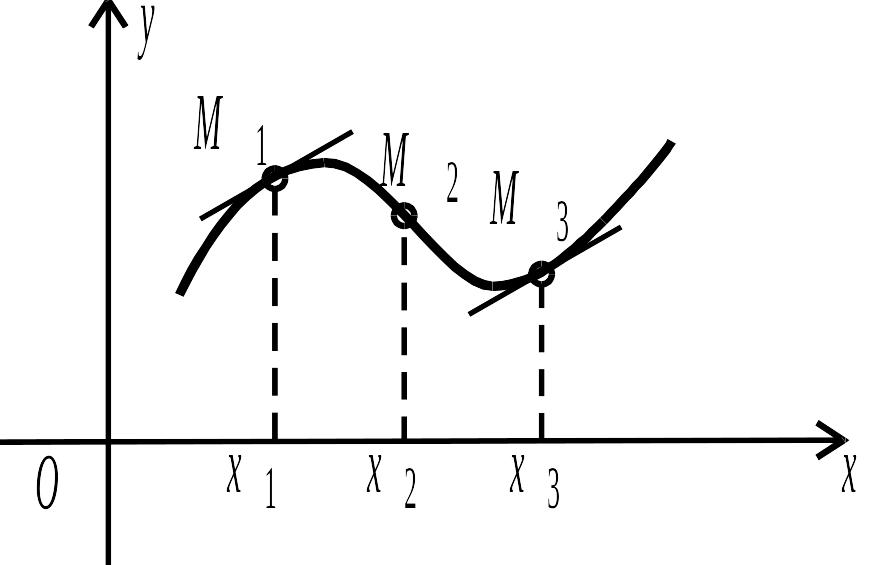

На рис. 3.15 у точці крива випукла, у точці увігнута.

Будемо називати криву випуклою (увігнутою) на деякому проміжку, якщо вона випукла (увігнута) у кожній точці цього проміжку.

Означення 3.7. Точка називається точкою перегину графіка функції, якщо в цій точці крива змінює випуклість на увігнутість чи навпаки.

На рисунку 3.15 такою точкою є точка .