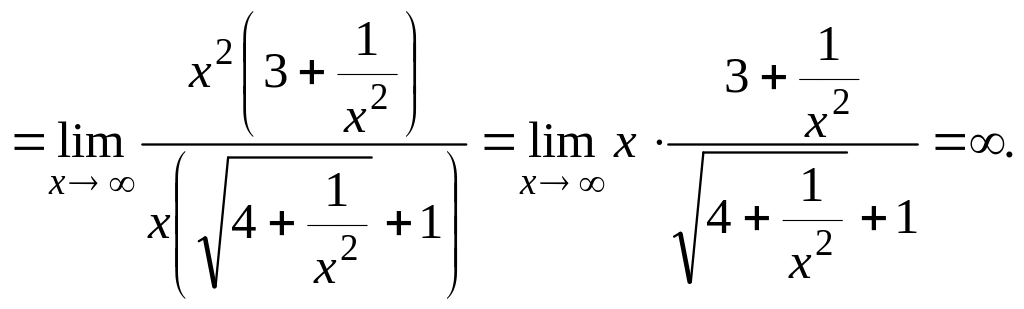- •Розділ 1. Теорія множин
- •1. Поняття множини
- •2. Найпростіші операції над множинами
- •3. Числові множини
- •4. Обмежені множини. Верхні та нижні грані множин
- •5. Поняття функції (відображення)
- •6. Еквівалентні множини. Потужність множин
- •7. Потужність континуума
- •Розділ 2. Послідовності. Функції однієї змінної
- •1. Числові послідовності
- •2. Границя послідовності
- •3. Застосування послідовностей в економіці
- •4. Поняття функції
- •5. Способи задання функції
- •6. Деякі властивості функцій
- •7. Функція, обернена до даної
- •8. Класифікація функцій
- •9. Основні методи побудови графіків функцій
- •10. Приклади застосування функцій в економіці
- •11. Границя функції
- •12. Нескінченно малі і нескінченно великі функції
- •13. Основні теореми про границі функцій
- •14. Обчислення границь функцій
- •15. Істотні границі Перша істотна границя
- •Друга істотна границя
- •16. Порівняння нескінченно малих
- •17. Неперервність функції в точці
- •18. Властивості функцій, неперервних в точці
- •19. Точки розриву і їхня класифікація
- •20. Властивості функцій, неперервних на відрізку
- •Розділ 3. Диференціальне числення функції однієї змінної
- •1. Задачі, що приводять до поняття похідної функції
- •2. Поняття похідної
- •3. Геометричний зміст похідної. Рівняння дотичної і нормалі до кривої
- •4. Диференційованість функції в точці
- •5. Похідні елементарних функцій
- •6. Основні правила диференціювання
- •7. Похідна складної функції
- •8. Логарифмічне диференціювання. Похідна степеневої, показникової, показниково-степеневої функцій
- •9. Похідна оберненої функції. Похідні обернених тригонометричних функцій
- •10. Таблиця похідних
- •11. Похідна неявно заданої функції
- •12. Похідна функції, заданої параметрично
- •13. Похідні вищих порядків
- •14. Наближені обчислення за допомогою похідної
- •15. Еластичність функції
- •Еластичності елементарних функцій:
- •16. Застосування еластичності в економічному аналізі Еластичність попиту відносно ціни
- •Еластичність і податкова політика
- •17. Основні теореми диференціального числення
- •18. Правило Лопіталя
- •19. Зростання і спадання функції на проміжку
- •20. Екстремуми функції
- •Необхідна умова екстремуму диференційованої функції.
- •Перша достатня умова екстремуму.
- •Друга достатня умова екстремуму.
- •Третя достатня умова екстремуму.
- •21. Найбільше і найменше значення функції на відрізку
- •22. Випуклість, увігнутість графіка функції. Перегин
- •Необхідна і достатня умова випуклості (увігнутості) графіка функції.
- •Необхідна умова точки перегину.
- •Достатні умови точки перегину.
- •23. Асимптоти графіка функції
- •24. Повне дослідження і побудова графіка функції
- •25. Застосування похідної в економіці Граничний аналіз в економіці.
- •Задачі на екстремум.
- •Розділ 4. Диференціальне числення функції багатьох змінних
- •1. Основні поняття
- •2. Границя і неперервність
- •3. Частинні похідні функції
- •4. Повний диференціал
- •5. Похідна функції за даним напрямком. Градієнт
- •6. Частинні похідні і диференціали вищих порядків
- •7. Локальний екстремум функції багатьох змінних
- •8. Неявно задані функції
- •9. Умовний екстремум
- •10. Найбільше і найменше значення функції в області
- •11. Метод найменших квадратів
- •12. Економічні задачі
13. Основні теореми про границі функцій
Теорема
2.2. Якщо число
є границею функції
при
,
то справедлива рівність
![]() ,
де
,
де
![]() при
– нескінченно мала функція.
при
– нескінченно мала функція.
Дійсно, якщо
![]() ,
виходить, що для кожного, як завгодно
малого, наперед заданого додатного
числа
можна вказати таке додатне число ,
що для всіх
,
що задовольняють нерівність
,
виконується умова
,
тобто функція
,
виходить, що для кожного, як завгодно
малого, наперед заданого додатного
числа
можна вказати таке додатне число ,
що для всіх
,
що задовольняють нерівність
,
виконується умова
,
тобто функція
![]() є нескінченно малою при
.
Назвемо її
.
Маємо
є нескінченно малою при
.
Назвемо її
.
Маємо
![]() ,
звідки
.
,
звідки
.
Легко довести і зворотне твердження: якщо функція представлена у вигляді суми сталої і нескінченно малої при функції, то ця постійна є границею функції при .
Теорема 2.3. Якщо функція має границю при , то вона єдина.
Припустимо, що при
функція має дві границі
![]() і
і
![]() ,
причому
,
причому
![]() .
Але тоді в силу теореми 2.2
.
Але тоді в силу теореми 2.2
![]() і
і
![]() ,
де
,
,
де
,
![]() – нескінченно малі при
функції. Віднімемо отримані рівності:
– нескінченно малі при
функції. Віднімемо отримані рівності:
![]() або
або
![]() .
Це можливо тільки при
.
Це можливо тільки при
![]() ,
оскільки
,
оскільки
![]() при
.
при
.
Теорема
2.4. Якщо
,
![]() ,
то:
,
то:
а)
![]() ;
;
б)
![]() ;
;
в)
 ,
якщо
,
якщо
![]() .
.
Сформулювати теорему можна так.
Якщо дві функції мають границі при , то границя їхньої алгебраїчної суми дорівнює алгебраїчній сумі границь цих функцій, границя добутку дорівнює добутку границь, границя частки дорівнює частці границь заданих функцій, за умови, що границя знаменника не дорівнює нулю при .
Доведемо теорему для випадку “а”.
Дійсно, оскільки
,
,
то на підставі теореми 2.2.
і
![]() ,
де
,
– нескінченно малі при
.
,
де
,
– нескінченно малі при
.
Але тоді
![]() ,
де
,
де
![]() – стала,
– стала,
![]() – нескінченно мала при
функція. Отже, відповідно до теореми
2.2 число
є границею функції
,
або
– нескінченно мала при
функція. Отже, відповідно до теореми
2.2 число
є границею функції
,
або
![]() .
Що і потрібно було довести.
.
Що і потрібно було довести.
Аналогічно доводиться теорема для випадку “б”.
Для випадку “в” дріб
![]() представимо у вигляді
представимо у вигляді
![]() ,
,
де функція
![]() є нескінченно малою при
.
є нескінченно малою при
.
Тому
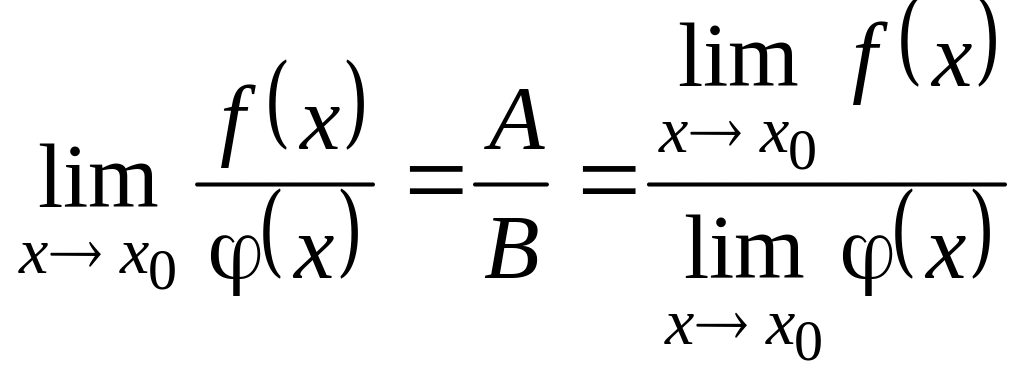 .
.
Наслідок. Сталі множники можна виносити за знак границі, тобто
![]() .
.
Теорема 2.5. Якщо в околі точки x0 виконуються нерівності
![]()
і
![]() ,
то і
.
,
то і
.
Для доведення розглянемо
– довільну, що збігається до
,
послідовність значень аргументу функцій
![]() і
і
![]() .
.
Відповідні послідовності
![]() і
і
![]() значень цих функцій мають границю, рівну
,
тобто
значень цих функцій мають границю, рівну
,
тобто
![]() ,
,
![]() при
при
![]() .
.
Використовуючи нерівності, дані в умовах теореми, можна записати
![]() .
.
Звідси
![]() ,
значить,
.
,
значить,
.
Зауваження. Усі теореми про границі вірні також і у випадку, якщо є одним із символів , , .
14. Обчислення границь функцій
На підставі теорем про границі, а також властивостей нескінченно малих і нескінченно великих функцій можна зробити наступний висновок: щоб обчислити границю функції при , необхідно у функцію підставити замість його граничне значення і обчислити результат.
Наприклад,
 .
.
Оформляють запис так:
![]() .
.
При обчисленні границі функції
![]() при
при
![]() в знаменнику дробу одержуємо нуль, тоді
результат обчислень беруть у квадратні
дужки, підкреслюючи символіку записів;
тут нуль є символом нескінченно малої.
Записують так:
в знаменнику дробу одержуємо нуль, тоді
результат обчислень беруть у квадратні
дужки, підкреслюючи символіку записів;
тут нуль є символом нескінченно малої.
Записують так:
![]() .
.
Якщо ж у результаті підстановки замість
його граничного значення
виходять так звані невизначеності
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
для обчислення границі приходиться
проводити перетворення функції, говорять,
“звільнятися від невизначеності”.
,
для обчислення границі приходиться
проводити перетворення функції, говорять,
“звільнятися від невизначеності”.
Зокрема, якщо невизначеність
отримана при обчисленні границі
дробово-раціональної чи дробово-ірраціональної
функції при
,
необхідно в чисельнику і знаменнику
дробу виділити нескінченно малу
![]() і скоротити на неї. Відзначимо, що ділення
чисельника і знаменника дробу на
нескінченно малу функцію можливо,
оскільки це не нуль, а реальна величина,
що змінюється так, що її значення можуть
бути як завгодно малими.
і скоротити на неї. Відзначимо, що ділення
чисельника і знаменника дробу на
нескінченно малу функцію можливо,
оскільки це не нуль, а реальна величина,
що змінюється так, що її значення можуть
бути як завгодно малими.
Приклад
2.7. Обчислити
![]() .
.
Розв’язання.
Безпосередня підстановка у функцію
граничного значення аргументу приводить
до невизначеності вигляду
.
Вирази чисельника і знаменника містять
у собі нескінченно малу
![]() :
:
![]() ,
,
![]() .
.
Тому
![]() .
.
Приклад
2.8. Обчислити
![]() .
.
Розв’язання.
Тут безпосередня підстановка у
функцію
![]() приводить до невизначеності
.
Щоб виділити в чисельнику нескінченно
малу при
приводить до невизначеності
.
Щоб виділити в чисельнику нескінченно
малу при
![]()
![]() помножимо чисельник і знаменник дробу
на вираз, спряжений чисельнику (позбудемося
від ірраціональності в чисельнику):
помножимо чисельник і знаменник дробу
на вираз, спряжений чисельнику (позбудемося
від ірраціональності в чисельнику):
![]() .
.
Тоді
![]()
![]() .
.
Розповсюджена границя відношення многочленів при прямуванні аргументу до нескінченності, що дає невизначеність :
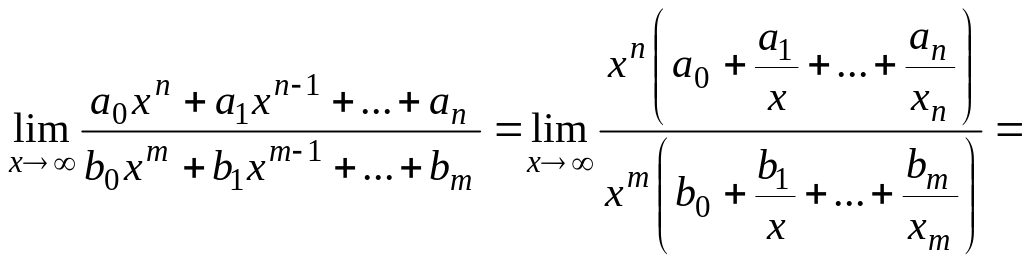
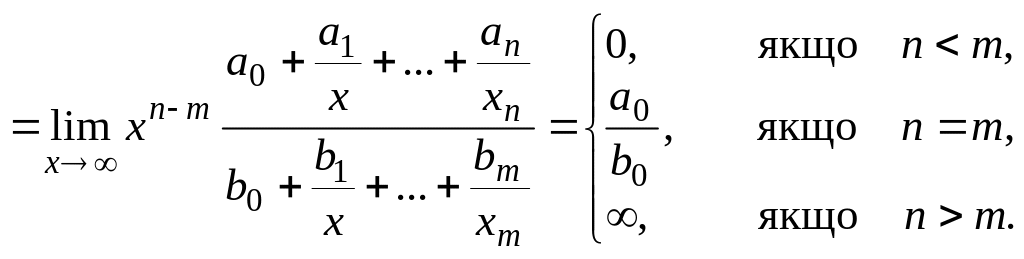
Тут
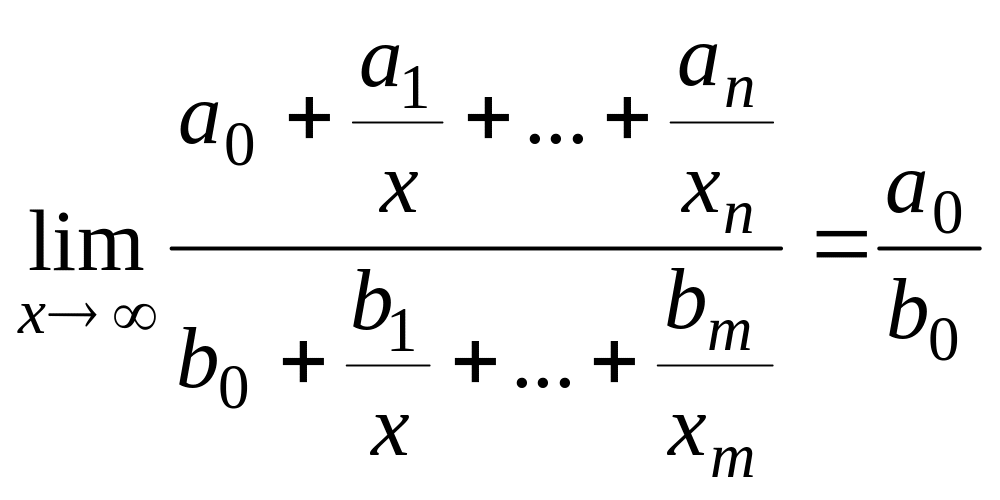 .
.
Наприклад,
![]() ,
,
![]() і т.д.
і т.д.
Невизначеності
![]() і
приводять до невизначеностей
або
,
перетворивши досліджувану функцію у
дріб.
і
приводять до невизначеностей
або
,
перетворивши досліджувану функцію у
дріб.
Приклад
2.9. Обчислити
![]() .
.
Розв’язання.
Безпосередньою підстановкою замість
x граничного значення одержимо
невизначеність
![]() .
.
Перетворимо досліджувану функцію,
помноживши і розділивши її на суму
![]() ,
одержимо
,
одержимо
![]() .
.
Тоді
![]()