128. 20. Екстремуми функції

Нехай функція неперервна на деякому інтервалі, що містить у собі точку .

Означення 3.5. Точка називається точкою максимуму функції , якщо існує такий окіл точки , що для всіх значень з цього околу виконується нерівність (рис. 3.9, а). Точка називається точкою мінімуму функції , якщо існує такий окіл точки , що для всіх значень цього околу виконується нерівність (рис. 3.9, б).

Точки максимуму і мінімуму функції називають точками екстремуму. Значення функції в точці максимуму (мінімуму) називають максимумом (мінімумом) функції чи екстремумом функції.

Функція на даному проміжку може мати і декілька екстремумів, причому деякі з мінімумів функції можуть бути більше деяких її максимумів.

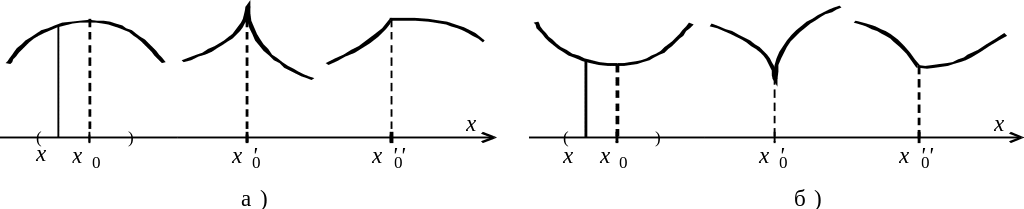
Рис. 3.9.

Рис. 3.10.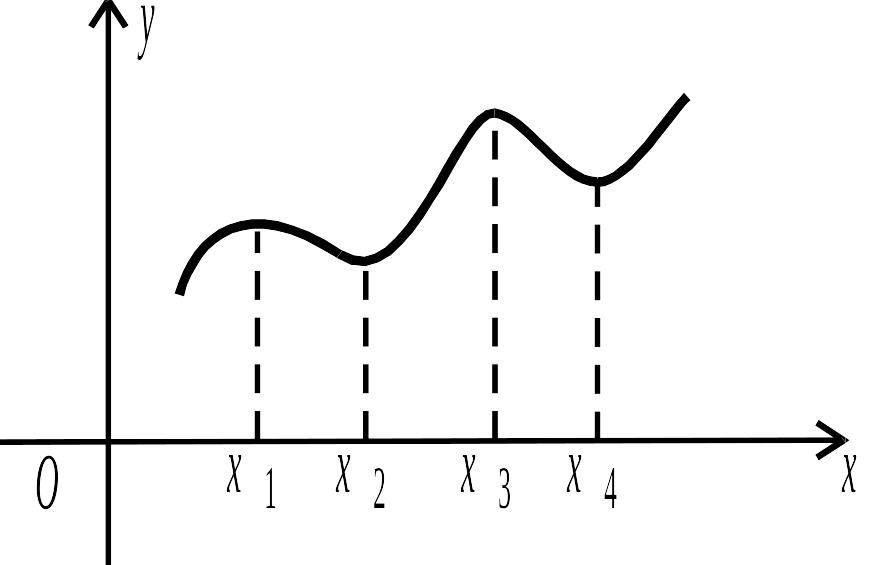

На рис. 3.10 зображена функція, у якої в точці максимум, а в точці – мінімум, причому . Але це не суперечить означенню екстремуму функції, оскільки в означенні екстремуму порівнюються значення функції в точці і деякому її околі. Говорять, що мова йде про локальні екстремуми.

Необхідна умова екстремуму диференційованої функції.

Якщо диференційована функція має в точці екстремум, то або не існує.

Нехай, наприклад, функція має в точці максимум. Тоді при досить малому маємо , тобто , отже відношення при , і при . Переходячи до границі при , одержимо , . За умовою функція диференційована в точці , отже одержані нерівності сумісні тільки при .

Аналогічно доводиться теорема, якщо в точці функція має мінімум.

Геометричний зміст доведеної умови полягає в тому, якщо в точках екстремуму функція має похідну, тобто диференційована, то дотична до кривої в цих точках буде паралельна вісі Ох. Такий екстремум називатимемо гладким.

Відзначимо, що наведена необхідна умова екстремуму диференційованої функції не є достатньою, тобто зворотне ствердження невірне. Похідна в точці може обертатися в нуль, а функція в цій точці може не мати екстремуму.

Наприклад, для функції при , але в цій точці функція не має екстремуму (рис. 3.11).

Рис. 3.11.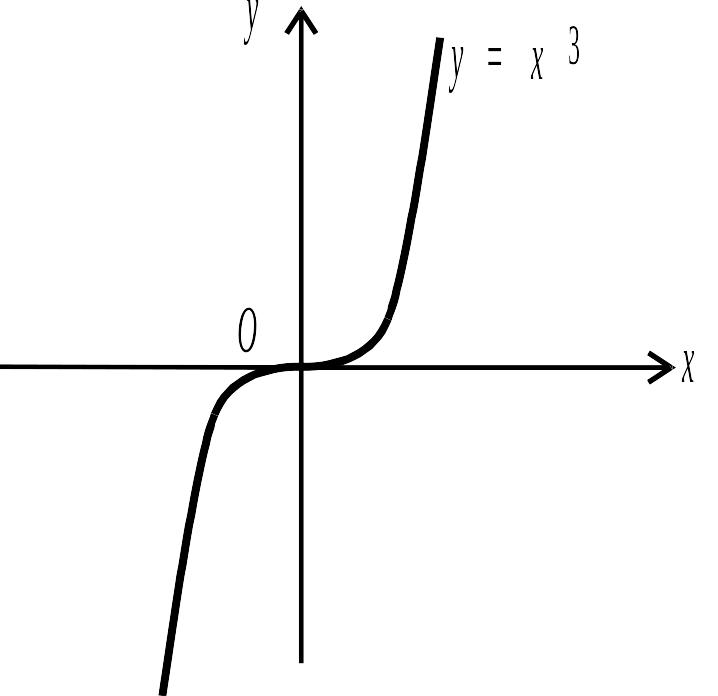

В цьому прикладі досліджували випадок, коли функція диференційована в точці і її околі. Але на рис. 3.9, а, б зображено графіки функцій, що мають у точках , екстремуми, але не мають скінченну похідну. Так, у точці похідна обертається в нескінченність, у точці похідна не існує. Такі екстремуми будемо називати гострими.

Таким чином, функція може мати екстремум як у точках, де похідна існує і дорівнює нулю чи нескінченності, так і в точках, де похідна не існує.

Перша достатня умова екстремуму.

Якщо функція неперервна в точці і її околі, диференційована в околі точки , крім, може бути, самої точки , і її похідна при переході через точку змінює знак з плюса на мінус, то функція має максимум у точці , якщо ж похідна при переході через точку змінює знак з мінуса на плюс, то в точці функція має мінімум.

Нехай, наприклад, при переході через точку похідна змінює знак з плюса на мінус. Тоді за теоремою Лагранжа для будь-якої точки з околу точки , де лежить між і .

Якщо , то і .

Якщо , то і .

Таким чином, в околі точки виконується нерівність чи , а це значить, що в точці функція має максимум.

Аналогічно розглядається випадок зміни знака похідної з мінуса на плюс.

Неважко бачити, що точка максимуму відокремлює інтервал зростання функції ( ) від інтервалу її спадання ( ), точка мінімуму відокремлює інтервал спадання від інтервалу зростання. Таким чином, якщо функція досліджена на зростання й спадання, то точки екстремуму визначаються автоматично.

Приклад 3.19. Знайти екстремуми функції .

Розв’язання. Для цієї функції проміжки зростання й спадання знайдені в прикладі 3.18.

Рис. 3.12.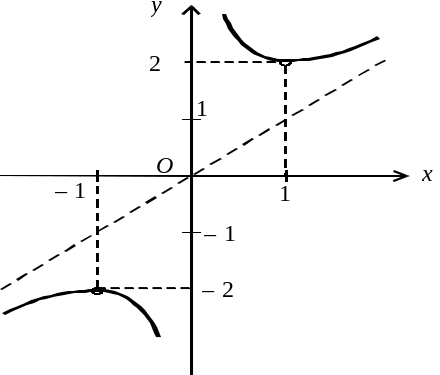

За результатами дослідження бачимо, що для точок виконується необхідна і достатня умови екстремуму, причому в точці функція має максимум, при цьому . У точці функція має мінімум, y(1)=2. Пишуть так: , .

Оскільки похідна , обидва екстремуми гладкі. Виходячи з того, що , , зобразимо графік функції схематично на рис. 3.12.

Приклад 3.20. Знайти екстремуми функції .

Розв’язання. Дана функція визначена на всій числовій прямій.

Похідна функції після перетворення має вигляд . Похідна дорівнює нулю в точці і не існує в точці . Розіб'ємо область визначення одержаними точками на проміжки і дослідимо знак похідної на проміжках. Результат відобразимо на схемі (рис. 3.13).

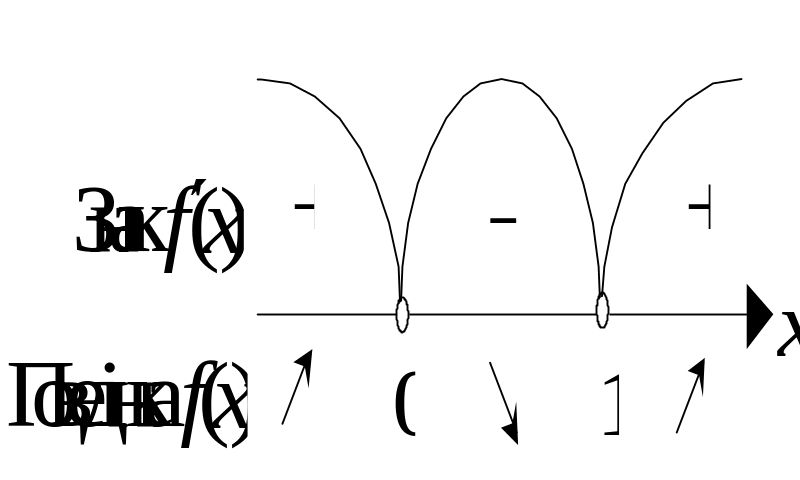
Рис. 3.13.

Рис. 3.14.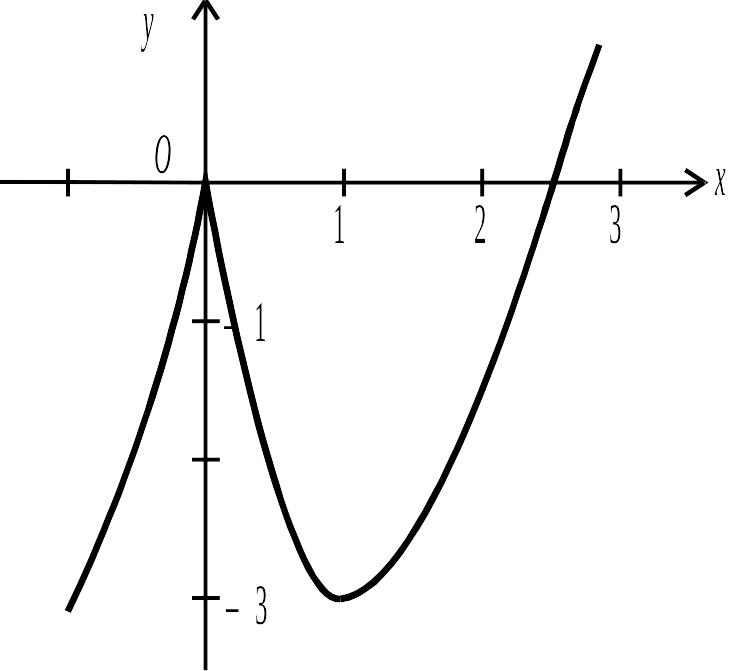

У точці функція визначена, похідна не є скінченною, тобто , дотична до графіка в точці з абсцисою перпендикулярна до вісі . При переході через точку похідна змінює знак з додатнього на від'ємний, отже в самій точці функція має гострий максимум: .

У точці функція визначена, похідна дорівнює нулю і при переході через точку змінює знак з мінуса на плюс, отже, тут функція має гладкий мінімум: .

Графік функції зображено на рис.3.14.