131. 23. Асимптоти графіка функції

Поняття асимптоти вже зустрічалося при вивченні гіперболи. Визначимо асимптоту кривої, заданої рівнянням .

Означення 3.8. Асимптотою кривої називається пряма (в загальному випадку крива), відстань до якої від точки даної кривої прямує до нуля при необмеженому віддалені цієї точки по кривій від початку координат (рис. 3.19).

Будемо розрізняти асимптоти вертикальні, горизонтальні і похилі.

Пряма є вертикальною асимптотою графіка функції , якщо .

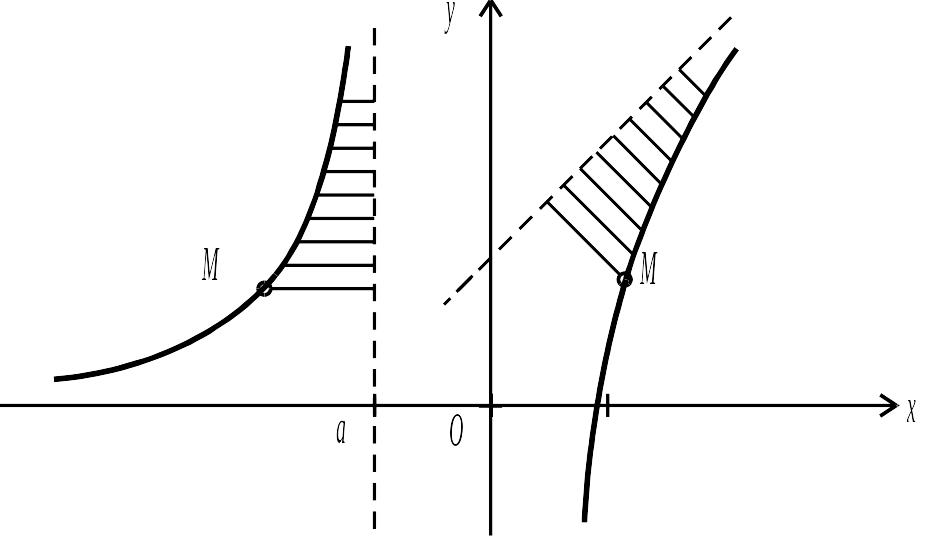
Рис. 3.19.

Очевидно, що вертикальні асимптоти функція може мати тільки в точках розриву або на границях області визначення.

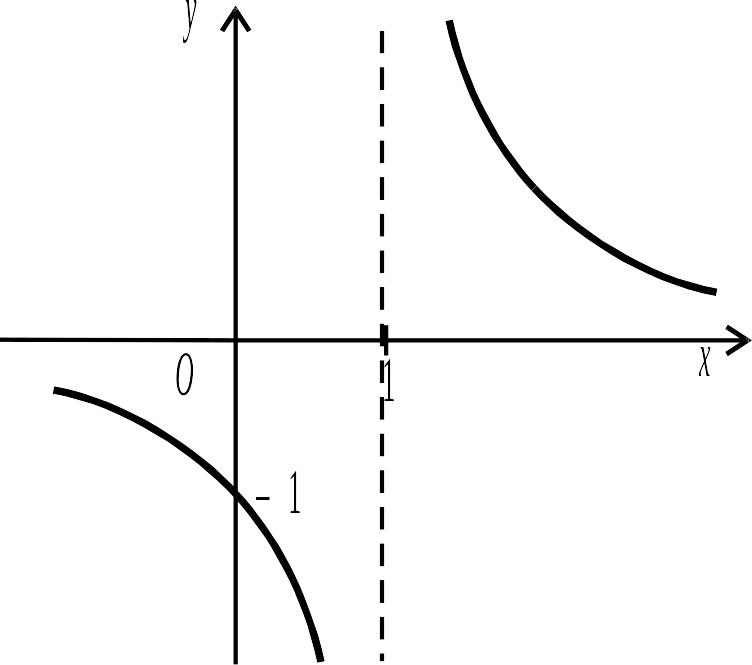
Наприклад, функція має вертикальну асимптоту , оскільки , . Графік функції зображено на рис. 3. 20.

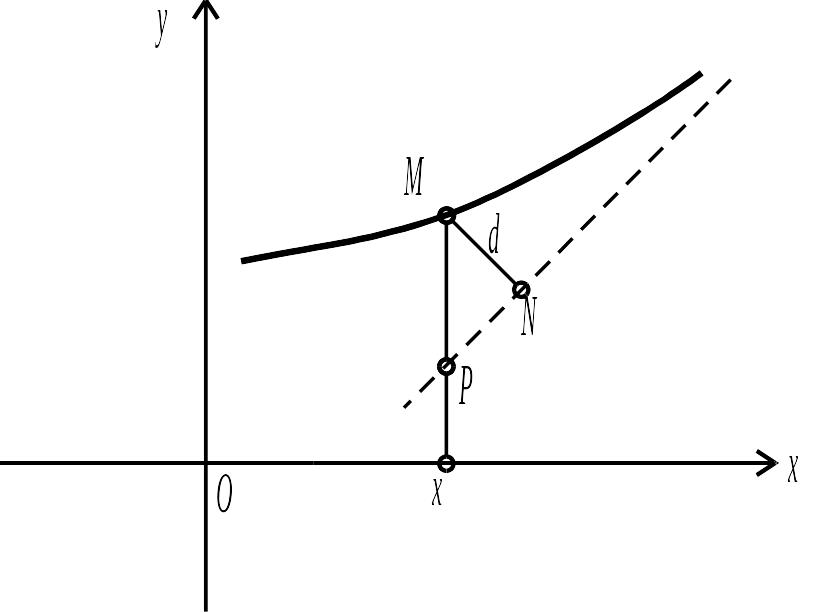
Нехай крива має похилу асимптоту. Знайдемо її рівняння у вигляді . Обчислимо коефіцієнти і так, щоб відстань довільної точки кривої до асимптоти при її віддалені по кривій до нескінченності прямувала до нуля (рис. 3.21).

Розглянемо різницю ординат графіка функції й асимптоти для одного значення аргументу :

.

Очевидно, якщо при , то і відстань точки графіка до асимптоти . Нехай

. (3.28)

Визначимо з останньої рівності і . Винесемо у виразі, що стоїть під знаком границі, за дужки і одержимо

.

Рис. 3.20.	Рис. 3.21.

Якщо , то очевидно, що . Оскільки , то

. (3.29)

Знаючи , з рівності (3.29) знаходимо

. (3.30)

Отже, якщо для функції пряма є асимптотою, то коефіцієнти і знаходяться за формулами (3.29) і (3.30).

Якщо , то рівняння приймає вигляд і асимптота називається горизонтальною.

Зауважимо, що якщо коефіцієнти і рівняння асимптоти існують і скінченні тільки при , то асимптота називається правою. Відповідно, якщо і існують і скінченні тільки при , асимптота називається лівою. При (або ) графік похилої асимптоти не має.

Приклад 3.23. Знайти асимптоти графіка функції

.

Розв’язання. Відзначимо, що задана функція визначена на всій числовій прямій, крім точки . Отже, якщо графік функції має вертикальну асимптоту, то її рівняння . Обчислимо однобічні границі функції в точці :

, .

Отже, пряма є вертикальною асимптотою графіка функції.

Рис. 3.22.

Рівняння похилої асимптоти знайдемо у вигляді .

Згідно з формулами .

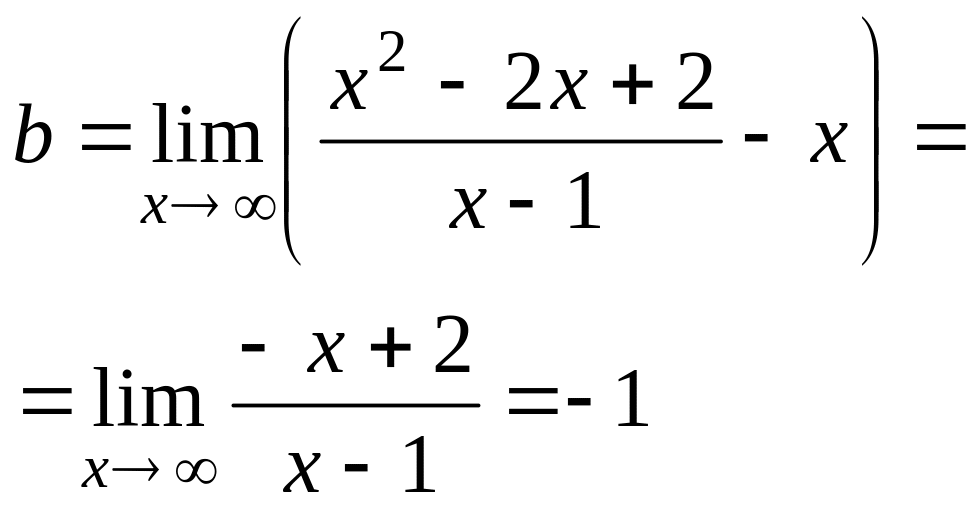
Отже, пряма є асимптотою графіка функції (рис. 3.22).

132. 24. Повне дослідження і побудова графіка функції

Повне дослідження функції припускає з'ясування таких її характеристик.

1. Область визначення функції.

2. Парність, непарність функції.

3. Нулі функції.

4. Асимптоти графіка функції (якщо графік не має похилих асимптот – з'ясувати поведінку функції на “кінцях” області визначення).

5. Проміжки монотонності і екстремуми функції.

6. Проміжки випуклості, увігнутості і точки перегину графіка функції.

7. Побудувати графік.

Якщо зазначених пунктів дослідження недостатньо для побудови графіка, є сенс додатково обчислити її значення в декількох точках області визначення.

Приклад 3.24. Дослідити функцію і побудувати її графік.

Розв’язання. Дослідимо функцію відповідно до запропонованої схеми.

1. Функція існує при всіх значеннях , крім , при якому знаменник дробу обертається в нуль. Таким чином, функція визначена в інтервалах .

2. Оскільки , то функція ні парна, ні непарна, графік її не симетричний.

3. Точку перетину з віссю визначимо, поклавши . Тоді , отже, точка належить графіку функції.

Точки перетину з віссю знайдемо, поклавши . Розв’язуючи рівняння , одержуємо .

4. Оскільки вертикальні асимптоти функція може мати тільки в точках розриву, обчислимо однобічні границі функції при :

, .

Тобто, пряма є вертикальною асимптотою графіка. Рівняння похилої асимптоти знайдемо у вигляді .

, .

Отже, пряма є похилою асимптотою графіка функції.

5. Обчислимо похідну: . Похідна дорівнює нулю в точках , . Похідна не існує в точці , але варто пам'ятати, що ця точка не належить області визначення функції.

Розіб'ємо область визначення отриманими точками на проміжки і дослідимо знак першої похідної в кожному проміжку. Результат відобразимо на схемі (рис. 3.23).

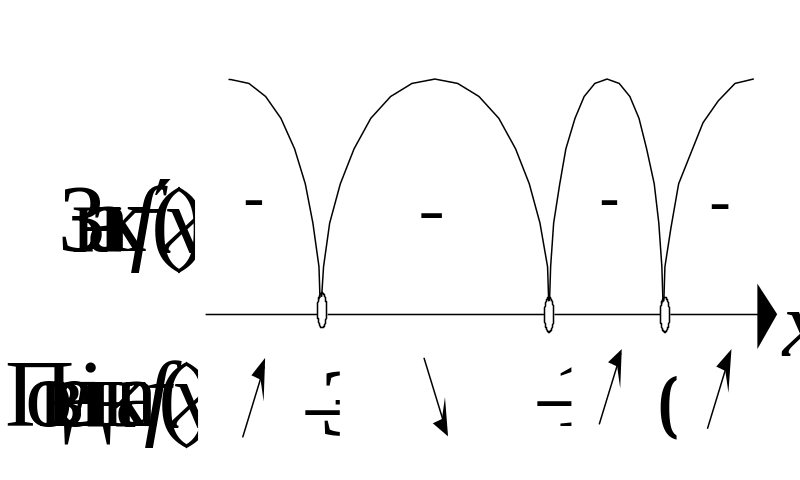
Рис. 3.23.

Функція зростає на проміжках і , спадає на проміжку . У точці функція має максимум: .

6. Обчислимо другу похідну: . Визначаємо критичні точки другого роду, поклавши чисельник і знаменник дробу рівними нулю. Одержимо , . Точка не може бути критичною, оскільки вона не належить області визначення.

Розіб'ємо область визначення одержаними точками на проміжки і дослідимо знак другої похідної на кожному проміжку. Результат зобразимо на схемі (рис. 3.24).

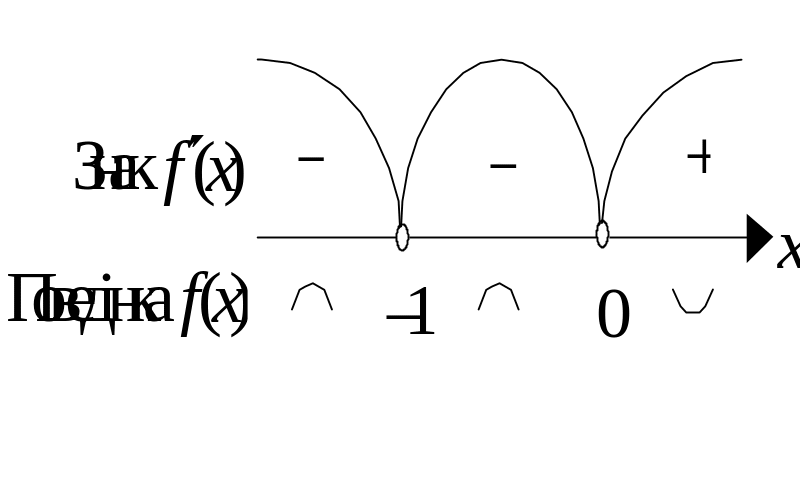
Рис. 3.24.

Рис. 3.25.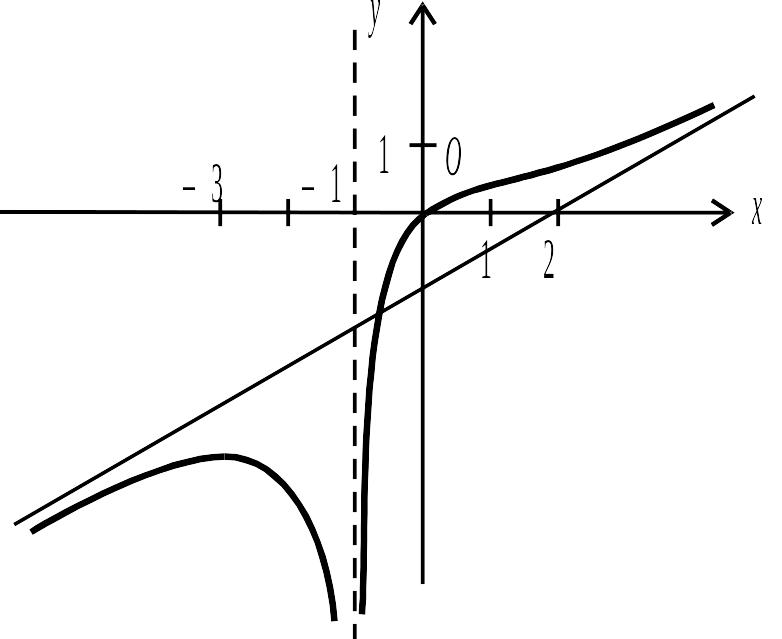

Графік функції випуклий на проміжках і й увігнутий на проміжку . При друга похідна дорівнює нулю і при переході через цю точку змінює знак. Це означає, що точка є точкою перегину.

Побудову графіка починаємо з зображення його асимптот і всіх точок, одержаних у процесі дослідження.

Графік функції зображено на рис. 3.25.