125. 17. Основні теореми диференціального числення

Теорема Лагранжа (теорема про скінченні прирости). Якщо функція неперервна на відрізку і диференційована у всіх внутрішніх точках цього відрізка, то усередині відрізка знайдеться хоча б одна така точка , що

. (3.24)

Дана теорема має просту геометричну інтерпретацію (рис. 3.5).

Рис. 3.5.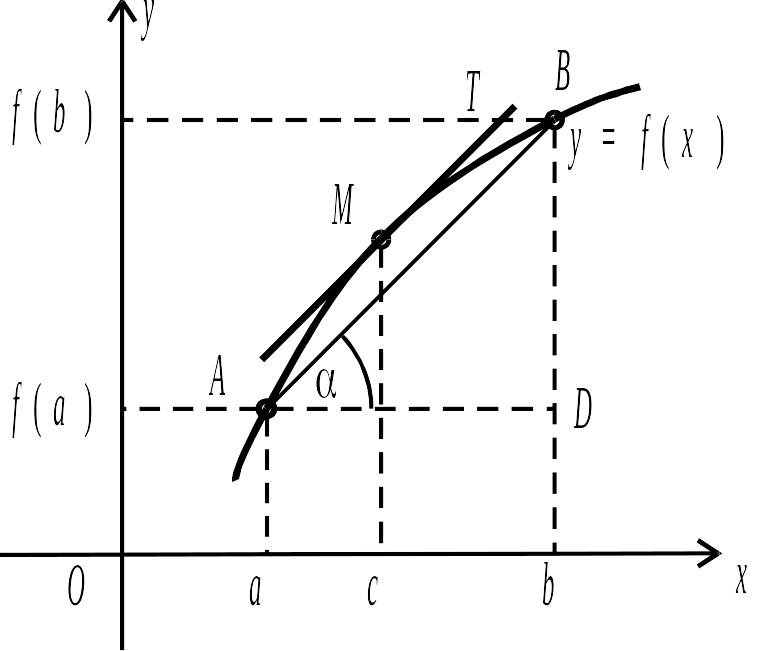

Проведемо січну . Координати точок і відповідно дорівнюють , і , . Очевидно, що кутовий коефіцієнт січної . Будемо переміщувати січну паралельно до її початкового положення, доки вона не перетвориться на дотичну до графіка функції в деякій його точці . Відповідно до побудови кутовий коефіцієнт січної дорівнює кутовому коефіцієнту дотичної , тому

.

Теорема Лагранжа може бути представлена у вигляді

, (3.25)

тобто якщо функція неперервна на відрізку і всередині нього в кожній точці має похідну, то приріст функції на цьому відрізку дорівнює добутку приросту аргументу на значення похідної в деякій точці , яка знаходиться між точками і .

Для довільного відрізка теорему Лагранжа можна записати у вигляді:

, де . (3.26)

Теорема Ролля (теорема про нулі похідної). Якщо функція неперервна на відрізку , має похідну в кожній внутрішній точці відрізка, причому на кінцях відрізка , то всередині відрізка знайдеться хоча б одна така точка , що похідна функції в цій точці буде дорівнювати нулю.

Справді, для функції виконуються умови теореми Лагранжа, значить, всередині відрізка знайдеться така точка , що . Оскільки , то .

Рис. 3.6.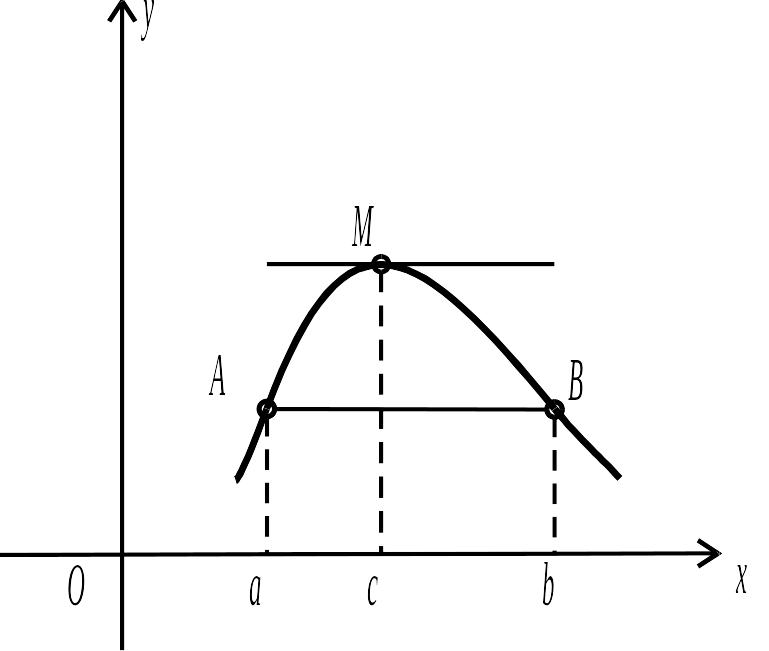

Геометрично теорема Ролля ілюструється просто: у точках і значення функції однакові, тобто точки і знаходяться на однаковій відстані від вісі і по один бік від неї (рис. 3.6). Отже, хорда паралельна вісі . Між цими точками на графіку функції існує хоча б одна точка , дотична в якій паралельна вісі .

Зокрема, якщо припустити, що , то теорему Ролля можна сформулювати так: між двома коренями функції знаходиться хоча б один корінь похідної, за умови, що функція неперервна на відрізку і в інтервалі існує її похідна.

Теорема Коші. Якщо кожна з двох диференційованих функцій і неперервні на відрізку , мають похідні в кожній внутрішній точці цього відрізка, причому , то всередині відрізка знайдеться хоча б одна така точка , що виконується рівність:

.

Зауважимо, що теорема Лагранжа є частинним випадком теореми Коші при .

126. 18. Правило Лопіталя

Нехай для функцій і виконується умова: . Тоді відношення втрачає зміст при , але границя відношення при може існувати. Наступна теорема, яку називають правилом Лопіталя, полегшує задачу обчислення цієї границі.

Правило Лопіталя.

Якщо функції і диференційовані в околі точки , неперервні в точці , відрізняється від нуля в точці і , то границя відношення функцій дорівнює границі відношення похідних цих функцій, якщо остання (скінченна або нескінченна) існує:

. (3.27)

Розглянемо відрізок , для якого виконуються умови теореми. Запишемо відношення у вигляді і застосуємо до різниць чисельника і знаменника теорему Лагранжа. Для функції знайдеться така точка , що . Для функції знайдеться така точка , що .

Тоді .

Нехай при відношення прямує до деякої границі. Оскільки точки і лежать між і , то при одержимо, що і , і отже, відношення прямує до тієї ж границі. Таким чином, при :

.

Якщо виявиться, що і нескінченно малі і диференційовані при , то правило Лопіталя можна застосовувати повторно.

Приклад 3.14. Обчислити .

Розв’язання. Функції і поблизу точки диференційовані, неперервні в точці , , тому можна застосувати правило Лопіталя.

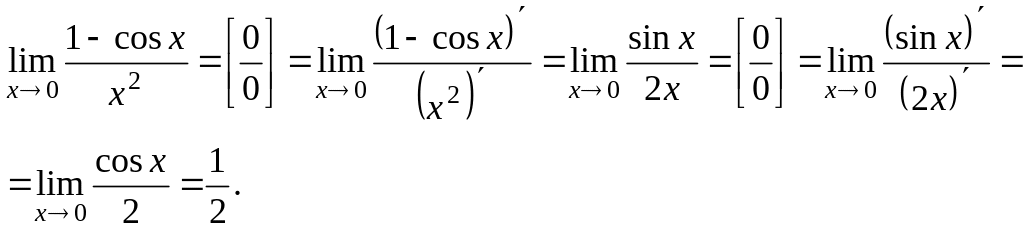
Покажемо, що правило Лопіталя справедливо і за умови, якщо – дорівнює , , .

Нехай, наприклад, умови теореми виконуються і .

Поклавши , одержимо, що при і тому, якщо існує границя відношення при , то існує і границя відношення функцій при і ці границі рівні. Теж саме можна сказати і про відношення їхніх похідних.

Функції , поблизу точки y=0 задовольняють умовам доведеної теореми, тому

,

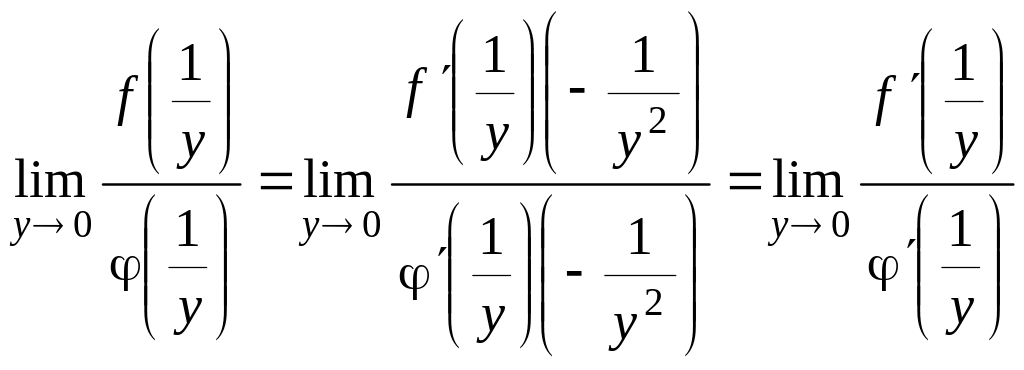звідки одержимо, що

.

Можна також показати, що правило Лопіталя можна застосувати й у випадку, якщо , тобто

.

Приклад 3.15. Обчислити .

Розв’язання. Для функції і при умови теореми виконуються, тому

Розкриття невизначеностей вигляду і можна привести до розглянутих вище невизначеностей, перетворивши досліджувану функцію на дріб.

Приклад 3.16. Обчислити границю .

Розв’язання. Безпосередньою підстановкою замість його граничного значення переконаємося в наявності невизначеності . Перейдемо до дробу, розділивши функцію на функцію , одержимо

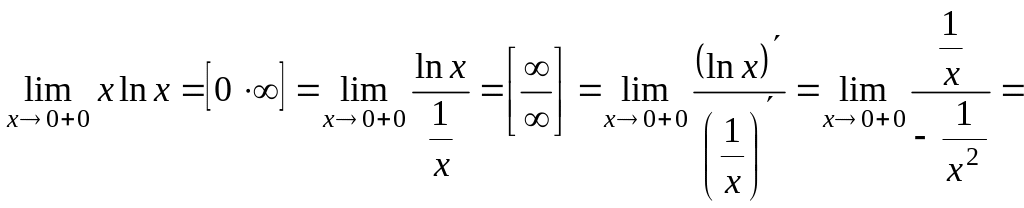
Правило Лопіталя дає можливість розкривати невизначеності вигляду , , . Такі невизначеності зустрічаються при обчисленні границі показниково-степеневої функції, тобто функції вигляду .

Для обчислення границі такої функції при досить знайти границю при функції . Тоді, якщо , то .

Приклад 3.17. Обчислити .

Розв’язання. Нехай , тоді і (див. приклад 3.16).

Отже, .