§4. Проекция вектора на ось и её свойства.

Пусть дан произвольный вектор . Пусть - произвольная ось. Обозначим через основания перпендикуляров, опущенных на ось из точек соответственно.

Проекцией вектора называется величина .

Проекцию вектора на ось будем обозначать символом . Построение проекции вектора на ось иллюстрируется на чертеже (1).

Рис.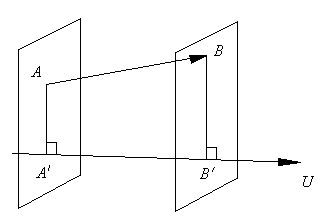

Углом наклона вектора к оси называется угол между двумя лучами, выходящими из произвольной точки , один из которых имеет направление, совпадающее с направлением вектора , а другой – направление, совпадающее с направлением оси .

Теорема 4.1. Проекция вектора на ось равна произведению длины вектора на косинус угла наклона вектора к оси .

Доказательство. Пусть – ось, проходящая через начало вектора и имеющая то же направление, что и ось . Пусть – основание перпендикуляра, опущенного из точки на ось . - основания перпендикуляров, опущенных из точек соответственно на ось . Тогда , где - величина направленного отрезка .

(Рис2)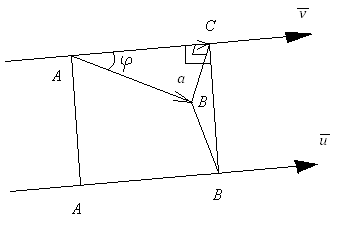

Возможны два случая. 1. Направленный отрезок имеет направление, совпадающее с направлением оси . (рис.2)

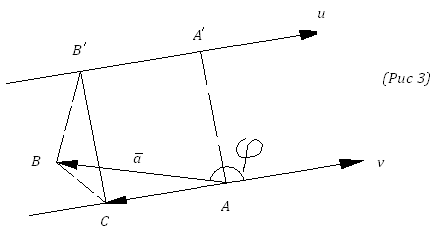
2. Направленный отрезок имеет направление противоположное к направлению оси . (рис.3).

Заметим, что в первом случае (рис 2) – угол наклона вектора к оси будет острым, во втором случае (рис 3) тупым.

Рассмотрим случай 1.

Для рассматриваемого случая имеем . Четырехугольник является прямоугольником. Поэтому .

Из прямоугольного треугольника имеем

Так как, по определению , из равенств (2), (3), (4) находим

Тем самым, для случая 1 теорема доказана. Случай 2 рассматривается аналогично.

Рассмотрим декартову прямоугольную систему координат с началом в точке и тройку векторов единичной длины, приложенных к точке , имеющих направления, совпадающие с направлениями этих осей соответственно.

Теорема 4.2. Для любого вектора существует единственная тройка чисел такая, что

при этом , , .

Доказательство. Приложим вектор в точке и проведём через его конец плоскости, параллельные координатным плоскостям . Точки пересечения этих плоскостей с осями обозначим соответственно .

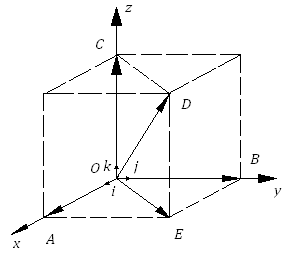
Очевидно, что . Т.к. , мы находим .

Из определения величины и из того, что следует, что . Так как проекция вектора на ось по определению есть величина , то из последнего равенства получим . Аналогично доказывается справедливость следующих равенств: = = . Учитывая эти равенства в равенстве (6), найдем

= + + . (7)

Введем обозначения , запишем равенство (7) в виде

Единственность легко получить с помощью геометрических рассуждений.

Числа , в равенстве (5) называются координатами вектора Тот факт, что являются координатами вектора , обозначается следующим образом: .

Теорема 4.3. Пусть в прямоугольной системе координат даны произвольные две точки , . Тогда координаты вектора соответственно равны

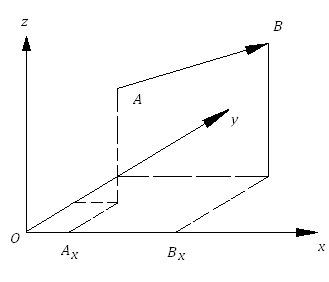
Доказательство. Обозначим через и основания перпендикуляров, опущенных из точек на ось . Тогда по определению , , где – величины направленных отрезков и

Согласно теореме 1.1 гл.3, величина направленного отрезка равна . С другой стороны величина является проекцией вектора на ось . Следовательно является координатой вектора . Аналогично доказывается равенство и .

Замечание. Если точки и расположены в плоскости , то для координат вектора справедливы равенства и .

Теорема 4.4. При сложении двух векторов и их координаты складываются. При умножении вектора на любое число 𝜆 все его координаты умножаются на это число.

Доказательство. Пусть , . Складывая эти равенства и пользуясь свойствами линейных операций, получим

.

Из последних равенств вытекает утверждение теоремы.

Теорема 4.5. При сложении двух векторов и их проекции на произвольную ось складываются. А при умножении вектора на любое число 𝜆 его проекция на произвольную ось умножается на число 𝜆.

Доказательство. Пусть даны произвольные векторы , и ось . Введём декартову прямоугольную систему координат так, чтобы ось совпадала с осью .

Пусть в введённой системе координат , . Тогда в силу теоремы 4.4

и .

Следовательно и Теорема доказана.