§2. Декартовы прямоугольные координаты на плоскости и в пространстве.

Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости. Одну из указанных осей называют осью или осью абсцисс, другую осью или осью ординат. Оси и называются также координатными осями. Пусть – основания перпендикуляров, опущенных из произвольной точки плоскости, на оси и соответственно. Декартовыми прямоугольными координатами точки будем называть величины направленных отрезков и осей и соответственно. Координаты точки называются соответственно абсциссой и ординатой. Тот факт, что точка имеет координаты , обозначается следующим образом: .

Аналогично вводятся декартовы прямоугольные координаты в пространстве.

Три взаимно перпендикулярные оси в пространстве с общим началом в точке и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве. Одну из указанных осей называют осью или осью абсцисс, другую осью или осью ординат, третью – или осью аппликат.

Пусть – основания перпендикуляров, опущенных из произвольной точки пространства на оси соответственно.

Декартовыми прямоугольными координатами точки будем называть соответственно величины направленных отрезков , и . Координаты называются соответственно абсциссой, ординатой и аппликатой точки . Тот факт. Что точка имеет координаты обозначается следующим образом .

§3. Понятие вектора и линейные операции над векторами.

Вектором называется произвольный направленный отрезок. В дальнейшем, для обозначения вектора, будем пользоваться символом , где – начало, а конец данного направленного отрезка, либо одной латинской буквой, снабженной чертой, либо просто жирной латинской буквой, например или На чертеже будем изображать вектор стрелкой, причём букву обозначающую этот вектор будем ставить у его конца.

Начало вектора называется точкой его приложения. Длина вектора обозначается следующим образом или .

Вектор называется нулевым, если начало и конец его совпадают. Нулевой вектор не имеет определённого направления и имеет длину равную нулю.

Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

Все нулевые векторы считаются равными.

Суммой двух векторов и называется вектор, идущий из начала вектора в конец вектора при условии, что вектор приложен к концу вектора .

Данное правило сложения двух векторов называется правилом треугольника.

Очевидно, что этот же вектор + для неколлинеарных векторов может быть получен, как диагональ параллелограмма, построенного на векторах

Это правило сложения векторов называется правилом параллелограмма.

Правило сложения векторов обладает следующими свойствами:

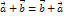1. (Коммутативность сложения)

2. (Ассоциативность сложения)

3. Существует нулевой вектор , такой что для любого вектора .

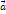4. Для любого вектора существует противоположный к нему вектор 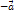, такой, что

.

Доказательство свойств 1 и 2 для неколлинеарных векторов проводится непосредственно построением.

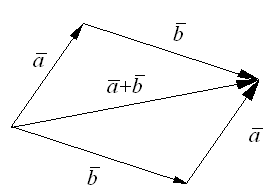
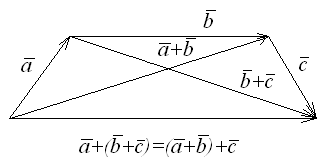
Для коллинеарных векторов свойства 1, 2 доказать самостоятельно.

Свойство 3 очевидно.

Свойство 4. Очевидно, так как для любого вектора существует вектор , такой что . Т.е. .

Разностью векторов и называется такой вектор , что .

Разность векторов обозначается .

Теорема 3.1. Для любых векторов существует и притом единственная разность

Доказательство. Рассмотрим вектор . Тогда . Следовательно существует разность .

Докажем единственность разности векторов . Пусть - разность векторов , тогда

Следовательно если - разность векторов , то . Единственность доказана.

Замечание. Правило параллелограмма сложения неколлинеарных векторов позволяет построить и разность , как другую диагональ параллелограмма.

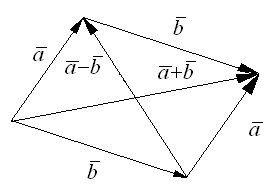
Свойства 1 -4 позволяют распространить правило сложения на сумму любого конечного числа векторов.

Сумма любого конечного числа векторов может быть построена с помощью следующего правила: если приложить вектор к концу вектора , вектор к концу вектора , …, вектор к концу вектора , то сумма представляет собой вектор, идущий из начала вектора к концу вектора .

Естественно назвать это правило сложения векторов правилом замыкания ломаной до многоугольника.

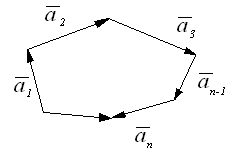
Произведением вектора на число называется вектор , коллинеарный вектору , имеющий длину и направление, совпадающее с направлением вектора в случае и противоположное направлению в случае .

Замечание. В случае, когда , или произведение представляет собой нулевой вектор, направление которого не определено.

Операция умножения вектора на число обладает следующими свойствами:

1. ;

2. 

3. 

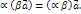
Свойства 5 – 7 доказываются одинаково. Приведём доказательство свойства 5 для неколлинеарных векторов и при условии (случай рассматривается аналогично).

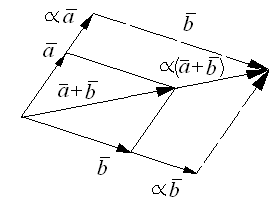
Приложим векторы в общую точку . Построим вектор , как диагональ параллелограмма, построенного на векторах . Пусть - конец вектора ( Т.к. , то векторы и ( имеют одинаковые направления. Пусть - точка пересечения прямой и прямой, проходящей через точку , параллельно вектору . - точка пересечения прямой и прямой, проходящей через точку параллельно вектору . Тогда четырёхугольник является параллелограммом. Следовательно

С другой стороны, из подобия треугольников , и треугольников следует, что

Из равенств (2) и (3) следует, что , . Т.к. и имеют одинаковые направления, получим Аналогично . Учитывая полученные выражения , найдем .

Доказательство свойства 5 для случая коллинеарных векторов и для случая привести самостоятельно.