47 Билет

. Понятие определённого интеграла.

1. Интегральная сумма и её предел.

Пусть функцию определёна на сегменте . Рассмотрим конечное множество точек сегмента , удовлетворяющих условиям

Множество точек , удовлетворяющих условиям (1) называется разбиением сегмента .

Сегмент , называется k-м частичным сегментом. Длину k -го частичного сегмента обозначим через , т.е. . Пусть – произвольная точка, принадлежащая k-му частичному сегменту

Составим для заданной функции и заданного разбиения (1) следующую сумму:

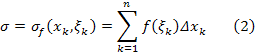
называемую интегральной суммой функции на сегменте , отвечающей данному разбиению (1) сегмента и данному выбору точек .

Обозначим через d Наибольшую длину частичных т.е. .

Число I называется пределом интегральных сумм (2) при стремлении к нулю наибольшей длины d частичных сегментов, если для любого положительного числа найдётся зависящее от положительное число такое, что для всех разбиений сегмента независимо от выбора точек , из неравенства следует неравенство

Функция называется интегрируемой на сегменте , если существует конечный предел

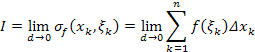
При этом указанный предел I называется определённым интегралом от функции по сегменту и обозначается символом

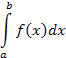
В этом обозначении функция называется подынтегральной функцией, число a – нижним пределом интегрирования, а число b – верхним пределом интегрирования.

Из определения следует, что определённый интеграл зависит только от функции и пределов интегрирования a и b и не зависит от выбора обозначения аргумента интегрирования, т.е.

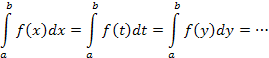
2. Верхние и нижние суммы.

Пусть функция определена и ограничена на сегменте . Тогда для произвольного разбиения (1), функция ограничена на каждом частичном сегменте . Обозначим через и соответственно точную верхнюю и точную нижнюю грани функции на частичном сегменте . Для произвольного разбиения сегмента рассмотрим следующие суммы:

Сумма (3) называется верхней суммой, отвечающей разбиению (1), а сумма (4) – нижней суммой, отвечающей

Справедлива следующая теорема:

Теорема 1.1 Для того, чтобы ограниченная на сегменте функция была интегрируема на этом сегменте, необходимо и достаточно, чтобы для любого существовало положительное число , такое, что для любого разбиения сегмента для которого наибольшая длина частичных сегментов меньше , выполнялось неравенство

Теорема . Если функция непрерывна на сегменте , то она интегрируема на указанном сегменте.

Теорема . Если функция интегрируема на сегменте то и функция интегрируема на этом сегменте.

Теорема (Необходимое условие интегрируемости).

Если функция интегрируема на сегменте , то она ограничена на этом сегменте.

Замечание 1. Условие ограниченности функции на сегменте является необходимым, но не достаточным условием интегрируемости данной функции на сегменте .

. Свойства определённого интеграла.

1) Примем как соглашение, что

и что для любой интегрируемой на сегменте функции

(2)

2) Свойство линейности. Если функции и интегрируемы на сегменте и и - произвольные вещественные числа, то функция интегрируема на сегменте , причём

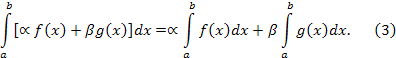
Действительно, пусть - произвольное разбиение сегмента . Рассмотрим интегральную сумму функции , отвечающую данному разбиению и произвольному выбору точек

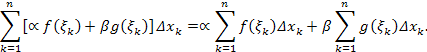
Из последнего равенства имеем

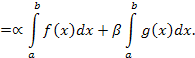
Что доказывает равенство (3).

Из свойства линейности следует, что для произвольной интегрируемой на сегменте функция и произвольного вещественного числа функция интегрируема на сегменте , при этом

.

3) Свойство аддитивности. Если и функция интегрируема на каждом из сегментов и , то

Действительно, возьмём произвольное разбиение сегмента , содержащее точку , т.е.

Возьмём произвольные точки , принадлежащие частичным сегментам и составим интегральную сумму, отвечающую данному разбиению сегмента .

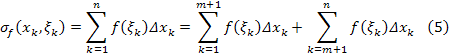
Очевидно, точки образуют разбиение отрезка , а точки - разбиение отрезка . Тогда, в силу интегрируемости функции на сегментах и существуют пределы интегральных сумм, стоящих в правой части равенства (5). Следовательно, существует предел интегральной суммы в правой части равенства (4) и справедливо равенство (4).

Замечание. При формулировке свойства 4), необязательно требовать интегрируемость функции на всех трёх сегментах и . Так как, можно доказать, что из интегрируемости функции на сегментах и следует её интегрируемость на сегменте и, наоборот, из интегрируемости функции на сегменте следует её интегрируемость на каждом из сегментов и

Геометрические и физические приложения определённого интеграла.