36 Билет
Понятие производной высших порядков.
Пусть функция определена и дифференцируема в каждой точке интервала . Тогда её производная сама является функцией, определённой на интервале .
Если
функция
имеет производную в некоторой точке x
интервала
,
то эту производную называют второй
производной или производной второго
порядка функции
в точке x
и обозначают символом 
или 
,
или 
,
,
.
После
введения понятия второй производной,
можно последовательно ввести понятие
третьей производной, затем четвёртой
производной и т.д. Если предположить,
что нами уже введено понятие 
-й
производной и что эта
-я
производная дифференцируема в некоторой
точке x
интервала 
,
т.е. имеет в этой точке производную, то
производную от
-й
производной называют -й производной
(или производной n-го
порядка) функции
в точке x
и обозначают символом 
или 
.
Итак по определению 
,
,
…, 
.
Функцию, имеющую на данном множестве X конечную производную n-го порядка называют n раз дифференцируемой на данном множестве.
Производные высших порядков находят многочисленные применения в физике. Например, физический смысл второй производной заключается в следующем: если функция определяет закон движения материальной точки по прямой, то первая производная равна мгновенной скорости движущейся точки в момент времени x, а вторая производная равна ускорению движущейся точки в момент времени x.
2. 
-е
производные некоторых функций.
В
ычислим
n
-ю производную степенной функции 
,
где
- любое действительное число. .
Отсюда легко усмотреть общий закон:
В
ычислим
n
-ю производную функции 
.
Вычислим n -ю производную функции .
Т.е.,
после каждого дифференцирования к
аргументу x
.
Отсюда
получается формула
Совершенно
аналогично выводится формула 
3. Формула Лейбница для n -й производной произведения двух функций.
Пусть
функции
и
n
раз дифференцируемы в точке x.
Тогда функция 
n
раз дифференцируема в точке x
и справедлива следующая формула
Это правило носит название формулы Лейбница.
Как
видим, формула (1) совпадает с формулой
разложения бинома 
,
лишь вместо степеней u
и v
стоят производные соответствующих
порядков.
Полагая,
что производная нулевого порядка функции
равна самой функции, т.е. 
,
формулу (1) можно записать в следующей
компактной форме:
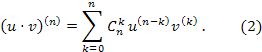
Формула (1) легко доказывается с помощью математической индукции.
Доказать
формулу (1) для 
самостоятельно.
4. Дифференциалы высших порядков.
В данном разделе мы будем использовать для обозначения дифференциала наряду с символом также символ .
Как уже известно, для первого дифференциала дифференцируемой в данной точке x функции справедливо равенство
Предположим, что правая часть равенства (3) является функцией аргумента x , дифференцируемой в данной точке x .
Для этого достаточно потребовать, чтобы функция была два раза дифференцируемой в данной точке x, а аргумент x являлся либо независимой переменной, либо дважды дифференцируемой функцией некоторой переменной t. При этих предположениях мы можем рассмотреть дифференциал
от обеих частей равенства (3).
Значение
дифференциала от первого дифференциала
(3) взятое при 
,
называется вторым дифференциалом
функции
(в данной точке x)
и обозначается символом 
.
Итак, по
определению 
.
Предположим,
что уже введён дифференциал 
порядка 
и что функция
является n
раз дифференцируемой в данной точке
x
, а её аргумент
является либо независимой переменной,
либо
раз дифференцируемой функцией некоторой
независимой переменной
.
З
начение
дифференциала
-го
порядка
,
взятое при
,
называется дифференциалом
-го порядка функции
в данной точке x
и обозначается символом 
.
Итак, по
определению 
.
При вычислении второго и последующих дифференциалов следует существенно различать два случая: 1) когда аргумент x является независимой переменной, 2) когда аргумент x является соответствующее число раз дифференцируемой функцией некоторой независимой переменной t.
В случае,
когда x
является независимой переменной, мы
имеем право считать, что dx
не зависит от x
и для всех x
равен одному и тому же приращению
аргумента
.
При этом мы имеем 
.
Тогда
Итак, в случае, когда аргумент x является независимой переменной, для второго дифференциала функции справедливо представление
По аналогии устанавливается, что в случае, когда аргумент x является независимой переменной, для n-го дифференциала n раз дифференцируемой функции справедливо представление
Таким образом, для случая, когда аргумент x является независимой переменной, производная порядка n функции равна отношению n -го дифференциала этой функции к n-й степени дифференциала аргумента, т.е.
Иной вид имеют представления второго и последующих дифференциалов в случае, когда аргумент x является соответствующее число раз дифференцируемой функцией независимой переменной t.
Пусть функция два раза дифференцируема в данной точке x, а её аргумент x является два раза дифференцируемой функцией некоторой независимой переменной t. Тогда из свойства инвариантности формы первого дифференциала имеем
Из последнего равенства находим
Т.е.,
Сравнивая равенства (5) и (6) мы видим, что в отличие от первого дифференциала, второй дифференциал не обладает свойством инвариантности формы.
Тем более не обладают свойством инвариантности формы последующие дифференциалы