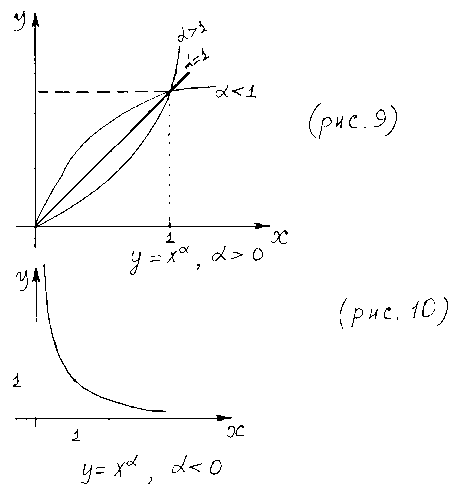- •2 Билет
- •3 Билет
- •4 Билет
- •5 Билет
- •§3. Элементарные преобразования системы линейных алгебраических уравнений.
- •§5.Системы общего вида
- •§4. Системы с верхней трапециевидной матрицей.
- •§6. Однородные системы линейных алгебраических уравнений.
- •6.Декартовы координаты на прямой.
- •§2. Декартовы прямоугольные координаты на плоскости и в пространстве.
- •§3. Понятие вектора и линейные операции над векторами.
- •§4. Проекция вектора на ось и её свойства.
- •7. Определение скалярного произведения
- •8.1. Расстояние между двумя точками
- •2. Деление отрезка в данном отношении.
- •Полярная система координат.
- •9.1. Параметрические уравнения прямой.
- •2. Каноническое уравнение прямой в плоскости.
- •3. Общее уравнение прямой в плоскости.
- •4. Уравнение прямой в отрезках.
- •5. Неполные уравнения прямой.
- •6. Уравнение прямой, проходящей через заданные две точки.
- •10. . Уравнение прямой с угловым коэффициентом.
- •10.. Условия пересечения, коллинеарности и ортогональности двух прямых. Угол между двумя пересекающимися прямыми.
- •11 Билет
- •12 Билет
- •13 Билет
- •14 Билет
- •15 Билет
- •16 Билет
- •17 Билет
- •18 Билет
- •19 Билет
- •20 Билет
- •21 Билет
- •22 Билет
- •23 Билет
- •24 Билет
- •25 Билет
- •26 Билет
- •27 Билет
- •28 Билет
- •29 Билет
- •30 Билет
- •31 Билет
- •32 Билет
- •33 Билет
- •34 Билет
- •35 Билет
- •36 Билет
- •37 Билет
- •38 Билет
- •39 Билет
- •40 Билет
- •2. Второе правило Лопиталя.
- •3. Другие виды неопределённостей и их раскрытие.
- •41 Билет
- •2. Другая запись формулы Тейлора и остаточного члена в форме пеано.
- •42 Билет
- •4. Разложение некоторых элементарных функций по формуле Маклорена.
- •43 Билет
- •2. Точки перегиба графика функции.
- •44 Билет
- •45 Билет
- •2. Неопределённый интеграл.
- •46 Билет
- •Интегрирование заменой переменной.
- •47 Билет
- •1. Площадь криволинейной трапеции.
- •48 Билет
- •49 Билет
- •§4. Основная формула интегрального исчисления.
- •50 Билет
- •Несобственный интеграл первого рода.
- •2. Несобственный интеграл II рода.
29 Билет
Понятие сложной функции.
Если
функция ![]() определена на некотором множестве
определена на некотором множестве ![]() ,
а на множестве
,
а на множестве ![]() -значений этой функции определена
функция
-значений этой функции определена
функция ![]() ,
то функция
,
то функция ![]() называется сложной функцией от
,
а переменная
называется сложной функцией от
,
а переменная ![]() - промежуточной переменной сложной
функции
- промежуточной переменной сложной
функции
Теорема
5.7.
(Теорема
о непрерывности сложной функции). Если
функция ![]() непрерывна в точке
,
а функция
непрерывна в точке
,
а функция ![]() непрерывна в точке
непрерывна в точке ![]() ,
то сложная функция
,
то сложная функция ![]() непрерывна в точке
.
непрерывна в точке
.
Доказательство.
Возьмём из области определения функции
произвольную последовательность
,
сходящуюся к точке
.
Тогда в силу непрерывности функции
в точке
имеем: ![]() ,
т.е. соответствующая последовательность
,
где
,
т.е. соответствующая последовательность
,
где
![]() сходится
к
сходится
к ![]() .
В силу непрерывности функции
в точке
получим
.
В силу непрерывности функции
в точке
получим
![]()
Следовательно,
предел функции ![]() в точке
равен её значению в этой точке, что
доказывает непрерывность функции
в точке
.
в точке
равен её значению в этой точке, что
доказывает непрерывность функции
в точке
.
Приведём
в качестве примера рассмотренную выше
функцию ![]() .
Эта функция непрерывна в каждой точке
действительной прямой
.
Эта функция непрерывна в каждой точке
действительной прямой ![]() ,
т.к. функция
,
т.к. функция ![]() непрерывна в любой точке
непрерывна в любой точке ![]() ,
а функция
,
а функция ![]() непрерывна в точке
непрерывна в точке ![]() .
.
Понятие обратной функции.
Пусть функция определена на множестве . Пусть для каждого y из области значения функции существует единственная точка из множества , такая, что . Тогда каждому элементу множества можно поставить в соответствие единственный элемент , такой, что .Следовательно, можно говорить о некоторой функции с областью определения и областью значений .
Эту
функцию назовём обратной к функции
и обозначим ![]() .
Итак, если
,
то
.
Итак, если
,
то ![]() .
Очевидно, что обратной к функции
.
Очевидно, что обратной к функции ![]() будет функция
.
будет функция
.
Теорема![]() (Теорема
о непрерывности обратной функции). Пусть
функция
непрерывна и возрастает (убывает) на
некотором сегменте
и
(Теорема
о непрерывности обратной функции). Пусть
функция
непрерывна и возрастает (убывает) на
некотором сегменте
и ![]() .
Тогда на сегменте
.
Тогда на сегменте ![]() (или
(или ![]() )
определена обратная функция
,
которая возрастает (убывает) и непрерывна
на сегменте
(
).
)
определена обратная функция
,
которая возрастает (убывает) и непрерывна
на сегменте
(
).
30 Билет
Непрерывность простейших элементарных функций.
![]() Показательная функция
Показательная функция ![]() непрерывна в каждой точке x
бесконечной прямой
непрерывна в каждой точке x
бесконечной прямой ![]() .
При этом функция
.
При этом функция ![]() возрастает при
возрастает при ![]() и убывает при
и убывает при ![]() .
Областью изменения функции
является множество
.
Областью изменения функции
является множество ![]() .
Графики функции
при
и при
изображены на рис.1 и 2.
.
Графики функции
при
и при
изображены на рис.1 и 2.
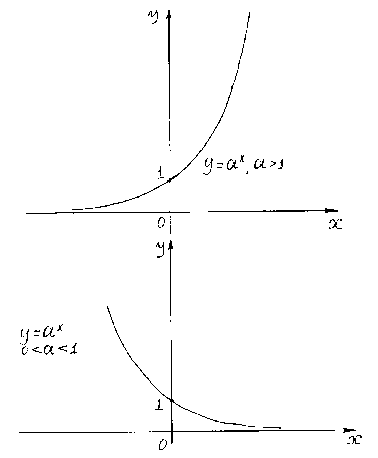
2.
Логарифмическая функция. Так как, на
произвольном сегменте ![]() бесконечной прямой
бесконечной прямой ![]() функция
функция![]() непрерывна и возрастает при
непрерывна и возрастает при ![]() (убывает
при
),
то в силу теоремы 5.8 для этой функции
существует на сегменте
(убывает
при
),
то в силу теоремы 5.8 для этой функции
существует на сегменте ![]() при
(
при
(![]() при
при
)
обратная функция ![]() ,
которая непрерывна и возрастает на
сегменте
при
(непрерывна и убывает на сегменте
,
которая непрерывна и возрастает на
сегменте
при
(непрерывна и убывает на сегменте ![]() при
).
Эта функция называется логарифмической
и обозначается символом
при
).
Эта функция называется логарифмической
и обозначается символом ![]() .
.
Поскольку
левый конец
мы можем неограниченно приближать к
![]() ,
а правый конец
,
а правый конец ![]() к
к ![]() ,
то в силу равенств
,
то в силу равенств ![]() ,
справедливых при
,
функция
будет определена и непрерывна на всей
открытой полупрямой
,
справедливых при
,
функция
будет определена и непрерывна на всей
открытой полупрямой ![]() и будет на этой полупрямой возрастать
при
(убывать при
).
Меняя для этой функции обозначение
аргумента
на
,
а обозначении функции
на
,
мы получим логарифмическую функцию
и будет на этой полупрямой возрастать
при
(убывать при
).
Меняя для этой функции обозначение
аргумента
на
,
а обозначении функции
на
,
мы получим логарифмическую функцию
![]() ,
которая определена и непрерывна на
открытой полупрямой
,
которая определена и непрерывна на
открытой полупрямой ![]() и на этой полупрямой возрастает при
(убывает при
)
и на этой полупрямой возрастает при
(убывает при
)
Графики логарифмической функции для и изображены на рис. 3 и 4.
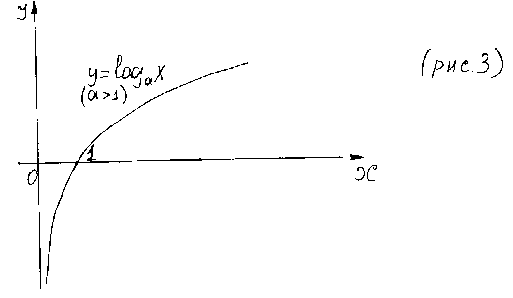
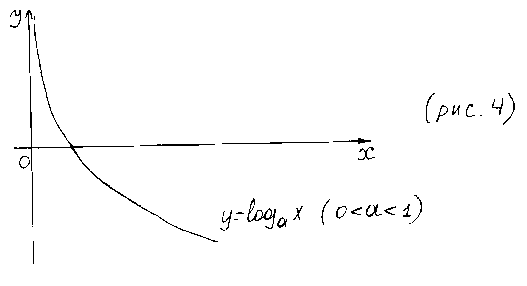
3.
Обратные тригонометрические функции.
Так как функция ![]() непрерывна и возрастает на сегменте
непрерывна и возрастает на сегменте
![]() и имеет множеством своих значений
сегмент
и имеет множеством своих значений
сегмент ![]() ,
то в силу теоремы 4.7 на сегменте
определена обратная функция
,
то в силу теоремы 4.7 на сегменте
определена обратная функция ![]() ,
которая непрерывна и возрастает на этом
сегменте. Меняя для этой функции
обозначение аргумента
на
,
а обозначении функции
на
,
мы придём к функции
,
которая непрерывна и возрастает на этом
сегменте. Меняя для этой функции
обозначение аргумента
на
,
а обозначении функции
на
,
мы придём к функции ![]() ,
непрерывной и возрастающей на сегменте
.
,
непрерывной и возрастающей на сегменте
.
Аналогично
устанавливается, что функция ![]() ,
обратная к непрерывной и убывающей на
сегменте
,
обратная к непрерывной и убывающей на
сегменте ![]() функции
функции ![]() ,
является непрерывной и убывающей на
сегменте
.
Функция
,
является непрерывной и убывающей на
сегменте
.
Функция ![]() ,
обратная к непрерывной и возрастающей
на интервале
,
обратная к непрерывной и возрастающей
на интервале ![]() функции
функции ![]() ,
является непрерывной и возрастающей
на бесконечной прямой
;
функция
,
является непрерывной и возрастающей
на бесконечной прямой
;
функция ![]() ,
обратная и непрерывная к непрерывной
и убывающей на интервале
,
обратная и непрерывная к непрерывной
и убывающей на интервале ![]() функции
функции ![]() ,
является непрерывной и убывающей на
бесконечной прямой
,
является непрерывной и убывающей на
бесконечной прямой ![]() .
.
Графики обратных тригонометрических функций изображены на рис. 5 – 8.
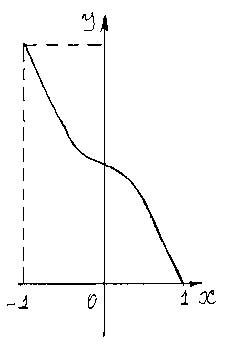
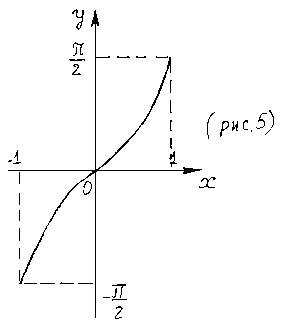
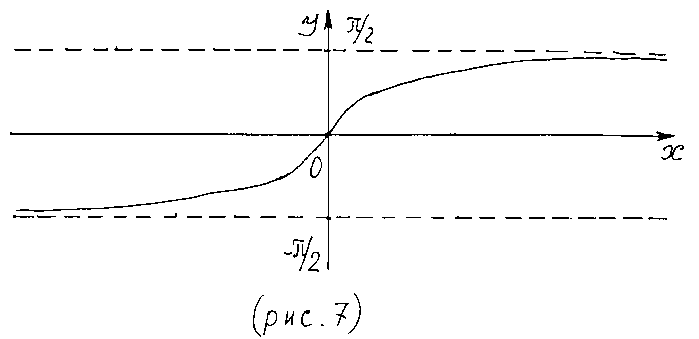
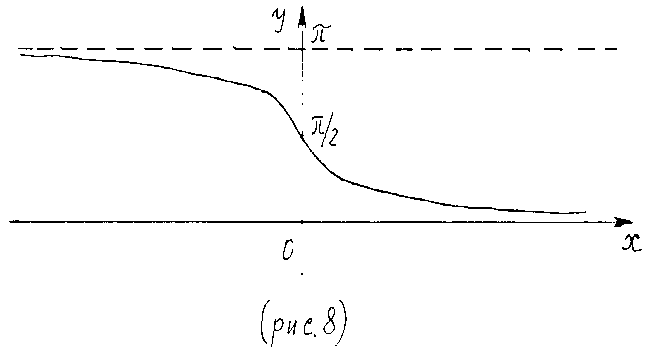
4.
Степенная функция. Пусть
![]() - произвольное фиксированное вещественное
число,
- некоторое вещественное число, большее
единицы.
- произвольное фиксированное вещественное
число,
- некоторое вещественное число, большее
единицы.
Пользуясь
основным логарифмическим тожеством
![]() ,
представим степенную функцию
,
представим степенную функцию ![]() в виде:
в виде:
![]()
т.е.
как сложную функцию вида ![]() ,
где
,
где ![]() .
.
Так
как
,
то функция ![]() возрастает на полупрямой
и потому функция
возрастает на полупрямой
и потому функция
возрастает при ![]() и убывает при
и убывает при ![]() на этой полупрямой. Отсюда и из того,
что функция
возрастает на всей прямой
на этой полупрямой. Отсюда и из того,
что функция
возрастает на всей прямой ![]() вытекает, что степенная функция
возрастает при
и убывает при
на полупрямой
.
вытекает, что степенная функция
возрастает при
и убывает при
на полупрямой
.
Далее,
из того, что функция
непрерывна в каждой точке
полупрямой
,
а функция
непрерывна в каждой точке ![]() бесконечной прямой
и из теоремы 5.7 о непрерывности сложной
функции вытекает, что степенная функция
непрерывна в каждой точке
полупрямой
.
бесконечной прямой
и из теоремы 5.7 о непрерывности сложной
функции вытекает, что степенная функция
непрерывна в каждой точке
полупрямой
.
На рис. 9 изображены графики функции для различных положительных значений .