10.. Условия пересечения, коллинеарности и ортогональности двух прямых. Угол между двумя пересекающимися прямыми.

Условие коллинеарности двух прямых.

Пусть прямые и заданные их общими уравнениями

Две прямые будем называть коллинеарными, если они либо параллельны, либо совпадают (сливаются).

Очевидно, что прямые, определяемые уравнениями (15) и (16) коллинеарны тогда и только тогда, когда коллинеарны их нормальные векторы , . Коллинеарность векторов означает существует такого действительного число 𝜆, что Следовательно прямые, заданные уравнениями (15) и (16), коллинеарны тогда и только тогда, когда выполнены равенства:

В случае , равенства (17) и (18) могут быть записаны в виде :

Равенство (19) является условием коллинеарности прямых и

Замечание. В равенстве (17) мы предполагаем, что . Если хотя бы один их коэффициентов обращается в ноль, например , то из равенства (17) имеем, что и .

Рассмотрим определитель

Если прямые и не коллинеарны, то нарушено равенство (19), тогда очевидно определитель .

Заметим, что является определителем основной матрицы системы линейных алгебраических уравнений

Данная система имеет единственное решение при условии, что и эти решения определяются формулами Крамера:

Итак, если прямые, лежащие в плоскости неколлинеарны, то координаты точки их пересечения находятся по формулам (21).

Если выполнено условие (19), то прямые и коллинеарны, т.е. они либо параллельны и не

имеют ни одной общей точки, либо эти прямые совпадают.

Пусть прямые и коллинеарны, т.е. выполнено равенство (19). Обозначим каждое из отношений (19) через , т.е. положим, что

Тогда справедливы равенства . Рассмотрим произвольную точку , лежащую на прямой . Тогда координаты точки удовлетворяют уравнению

Пользуясь равенствами (23), получим

Могут представиться два случая.

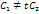1. , тогда из равенства (24) найдём

. Из последних соотношений имеем

Следовательно в случае, когда , произвольная точка прямой не лежит на прямой , т.е. у прямых нет общих точек. Следовательно, условие

(25)

является условием параллельности прямых .

2. Пусть теперь 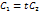, где – величина, указанная в равенствах (21). Тогда из равенства (24) получим

, т.е. точка лежит как на прямой , так и на прямой . Следовательно эти прямые сливаются.

Итак, мы получили следующее условие слияния двух прямых

Заметим, что при выполнении условия (25) система линейных уравнений (20) не имеет решений, а при выполнении условия (26) имеет бесконечное множество решений.

Условие ортогональности двух прямых.

Любые две пересекающиеся в одной точке прямые образуют два угла, в сумме равных 𝜋. Один из указанных углов совпадает с углом между нормальными векторами и этих прямых.

Найдём угол между векторами и

Пусть прямые заданы их общими уравнениями (15) и (16), тогда , . Обозначим через угол между векторами и Косинус этого угла может быть вычислен по формуле:

Учитывая в этой формуле, что

, ,

получим

В частности, если угол прямой, то и мы получим условие ортогональности прямых

(28)

Пусть теперь прямые заданы их уравнениями с угловыми коэффициентами

Запишем уравнения (27) и (28) в виде

Уравнения (31) и (32) являются общими уравнениями прямых при , , , , , . При этом из условия (25) получим условие параллельности прямых

Из условия (26) получим условие слияния двух прямых

.

Из формулы (27) получим формулу для определения угла между прямыми

Из условия (28) получим условие ортогональности прямых

Рассмотрим теперь случай, когда прямые заданы их каноническими уравнениями.

Из уравнений (37) и (38) получим

Уравнения (39) и (40) являются общими уравнениями прямых при

. Тогда из условий (25), (26), (27), (28) получим

1. Условие коллинеарности .

2. Условие параллельности .

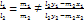3. Условие слияния .

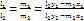4. Формула для вычисления угла .

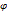
5. Условие ортогональности .

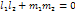Приведём ещё одну формулу для нахождения угла между двумя прямыми.

Пусть прямые заданы уравнениями

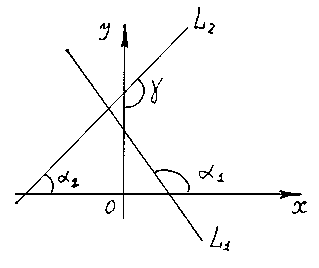
Пусть - угол между прямыми , отсчитанный от прямой до прямой против часовой стрелки. Тогда , либо , либо . Но во всех указанных случаях . Учитывая в последнем равенстве, что , , получим