7. Вынужденные колебания

Чтобы в реальной механической колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью периодически действующей вынуждающей силы, изменяющейся по гармоническому закону:

(11.50)

С учетом силы (11.50) закон движения для пружинного маятника запишется в виде.

Используя соответствующие обозначения, придем к уравнению

(11.51)

Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными механическими колебаниями.

Решение уравнения (11.51) равно сумме общего решения однородного уравнения (11.47) и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме. Заменим правую часть уравнения (11.51) на комплексную величину :

(11.52)

Частное решение этого уравнения будем искать в виде

Найдем производные для : 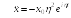. Подставляя выражение для и его производных в уравнение (11.52), получим

(11.53)

Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что . Тогда (11.53) имеет вид Найдем отсюда величину x₀ : Оно имеет вид

Это комплексное число удобно представить в экспоненциальной форме: где

(11.54)

и (11.55)

Следовательно, решение уравнения (11.53) в комплексной форме примет вид:

Его вещественная часть равна

_, (11.56)

где и задаются соответственно формулами (11.54) и (11.55).

Таким образом, частное решение неоднородного уравнения (11.52) имеет вид

(11.57)

Решение уравнения (11.52) равно сумме общего решения однородного уравнения

(11.58)

и частного решения (11.57). Слагаемое (11.58) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (11.54). Следовательно, в установившемся режиме вынужденные колебания происходят с частотой и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (11.54) и (11.55), также зависят от .

8. Амплитуда и фаза вынужденных колебаний. Резонанс

Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты .

Из формулы (11.54) следует, что амплитуда А смещения имеет максимум. Чтобы определить резонансную частоту – частоту, при которой амплитуда А смещения достигает максимума, – нужно найти максимум функции (11.54), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по и приравняв нулю, получим условие, определяющее : .

Это равенство выполняется при и , у которых только лишь положительное значение имеет физический смысл. Следовательно, резонансная частота

(11.59)

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте называется механическим резонансом. При значение практически совпадает с собственной частотой колебательной системы. Подставляя (11.59) в формулу (11.54), получим

(11.60)

На рис. 11.7 приведена зависимость амплитуды вынужденных колебаний от частоты при различных значениях .

Рис.11.7

Из (11.59) и (11.60) вытекает, что чем меньше , тем выше и правее лежит максимум данной кривой. Если , то все кривые приходят к одному и тому же, отличному от нуля, предельному значению , так называемому статическому отклонению. Если , то все кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

Из формулы (11.60) вытекает, что при малом затухании () резонансная амплитуда смещения , где Q – добротность колебательной системы, – статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше . На рис. 11.8 представлены резонансные кривые для амплитуды скорости. Амплитуда скорости 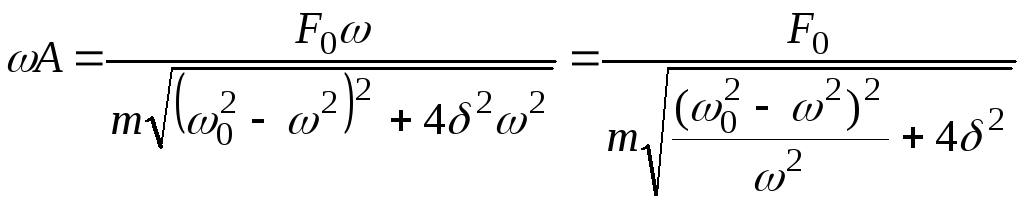максимальна при и равна , т.е. чем больше коэффициент затухания, тем ниже максимум резонансной кривой.

Из выражения 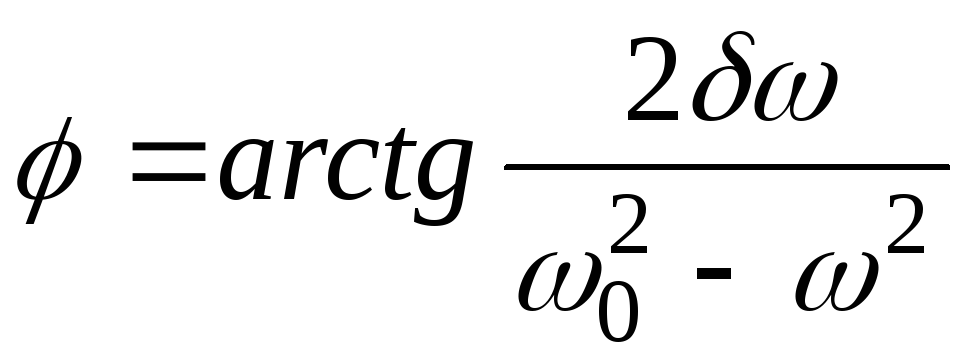следует, что если затухание в системе отсутствует, то только в этом случае колебания и вынуждающая сила имеют одинаковые фазы.

Рис.11.8

Зависимость от при разных коэффициентах представлена на рис.11.9. Отсюда следует, что при изменении изменяется и сдвиг фаз . Из формулы (11.55) вытекает, что при , а при независимо от значения коэффициента затухания , т.е. сила опережает по фазе колебания на р/2. При дальнейшем увеличении щ сдвиг фаз возрастает и при , т.е. фаза колебаний почти противоположна фазе внешней силы. Семейство кривых, изображенных на рис. 11.9, называется фазовыми резонансными кривыми.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника, используют явление резонанса.

Рис.11.9