2. Энергия и работа
Энергией называют физическую величину, являющуюся общей количественной мерой различных форм движения и существования материи, происходящих в результате совершения работы.
Таким
образом, энергия является функцией
состояния тела, например, движение тела
приводит к изменению его энергии. Сам
процесс изменения есть результат работы:
.
Катящийся шар, сталкиваясь с некоторым телом, перемещает его, т.е. совершает работу. Следовательно, катящийся шар обладает энергией. Кроме того, катящийся шар обладает энергией независимо от того, совершает он в данный момент работу или нет: энергия характеризует состояние системы, способность (возможность) системы к совершению работы при переходе из одного состояния в другое.
В физике в соответствии с различными физическими процессами и взаимодействиями различают механическую, тепловую, электромагнитную, ядерную и другие энергии.
Механическая энергия состоит из кинетической и потенциальной энергий.
3. Кинетическая энергия и работа
Пусть
под действием некоторой силы
тело (материальная точка) массой
совершает перемещение, изменив скорость
от
до
,
т.е. движется с ускорением
.
Напишем уравнение движения тела:
(6.9)
Учитывая
определение ускорения материальной
точки и умножив уравнение (6.9) на
перемещение точки
,
получим
(6.10)
Проинтегрировав
соотношение
с учетом изменения скорости тела, имеем
.
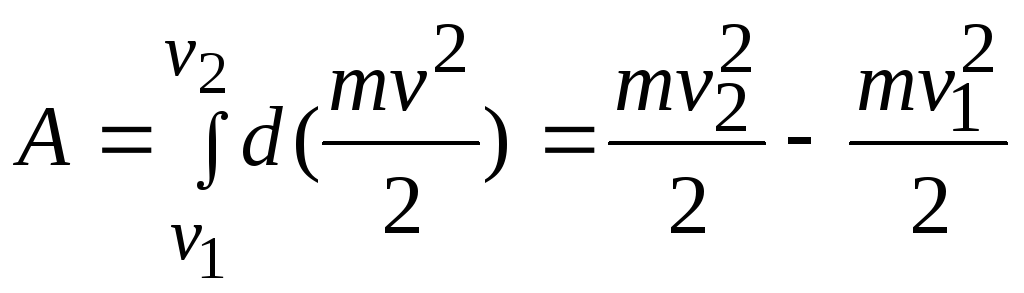Введем
обозначение
,
которое называется кинетической
энергией тела.
Итак, совершенная силой работа равна приращению кинетической энергии тела:
(6.11)
В этом заключается и физический смысл работы.
Из определения следует, что:
-
кинетическая энергия – это энергия движения;
-
кинетическая энергия – скалярная величина;
-
кинетическая энергия системы материальных точек равна сумме кинетических энергий всех точек, составляющих систему;
-
измеряется в тех же единицах, что и работа.
4. Потенциальная энергия
Потенциальная энергия обусловлена характером взаимодействия между телами, их взаимным расположением. Поэтому вид формулы для потенциальной энергии зависит от конкретного вида взаимодействия тел.
Так,
например, работа силы тяжести, необходимая
для изменения положения тела относительно
Земли, равна:
,
где
–
начальная и конечная высота (
)
тела относительно Земли. Выражение
называется потенциальной энергией силы
тяжести. Эта работа равна изменению
потенциальной энергии тела:
(6.12)
Положительная
работа сил тяжести соответствует убыли
потенциальной энергии. Наоборот, если
бы тело поднималось над поверхностью
Земли, приращение потенциальной энергии
соответствовало бы отрицательной
работе. Поэтому в общем случае следует
записать:
.
Так как
,
то
и
(6.13)
Формула (6.13) показывает, что консервативная сила – сила тяжести – равна градиенту потенциальной энергии, взятому с обратным знаком:
(6.14)
Эта формула связывает между собой силу и соответствующую ей потенциальную энергию, что дает возможность вычислить потенциальную энергию в каждом конкретном случае вида взаимодействия тел.
Пример.
Пусть задана сила всемирного тяготения
.
Так как
,
из формулы (6.13) найдем
.
Обычно
за начальную конфигурацию системы,
состоящую из двух материальных точек,
взаимодействующих между собой силами
всемирного тяготения, принимают
расположение этих точек на бесконечно
большом расстоянии друг от друга, где
=0.
Тогда потенциальная энергия взаимодействия
точек равна
(6.15)
Как и закон всемирного тяготения, эта формула верна не только для материальных точек, но и для любых сферически симметричных тел.
Физически знак минус обусловлен тем, что по мере самопроизвольного сближения тяготеющих тел их потенциальная энергия должна уменьшаться, переходя в кинетическую. Из формулы (6.15) следует, что максимальное значение потенциальной энергии тяготеющие тела будут иметь в том случае, когда они бесконечно удалены друг от друга.
Выше мы говорили о потенциальных и консервативных силах. Они тождественны лишь в случае стационарного силового поля, т.е. поля, остающегося постоянным во времени. Поле консервативных сил является частным случаем потенциального силового поля. Для нестационарного силового поля, т.е. поля, изменяющегося во времени, формула (6.14) не выполняется. Поэтому отождествлять потенциальные и консервативные силы нельзя.