
- •Основы теории автоматического управления
- •Содержание
- •Предисловие
- •Введение
- •0 Общие сведения о системах управления
- •Принцип действия и функциональная схема сау.
- •0.1 Классификация сау
- •0.1.1 Классификация сау по принципу действия
- •0.1.2 Классификация сау по характеру изменения выходной переменной
- •0.1.3 Классификация сау по математическому описанию
- •1 Линейные системы управления
- •1.1 Линеаризация нелинейных уравнений
- •1.2 Две формы записи линейных дифференциальных уравнений
- •1.3 Классификация динамических звеньев
- •1.4 Динамические характеристики звеньев
- •1.4.1 Временные динамические характеристики
- •1.4.2 Частотные динамические характеристики
- •1.5 Типы соединения звеньев в сау
- •1.5.1 Последовательное соединение звеньев
- •1.5.2 Параллельное соединение звеньев
- •1.5.3 Встречно-параллельное соединение звеньев
- •1.6 Основные правила преобразования структурных схем
- •1.7 Передаточные функции замкнутых сау
- •1.8 Устойчивость движения непрерывных линейных сау
- •1.8.1 Корневые критерии устойчивости
- •1.8.2 Коэффициентные (алгебраические) критерии устойчивости
- •1.8.2.1 Критерий о необходимых условиях устойчивости
- •1.8.2.2 Критерий Рауса-Гурвица
- •1.8.3 Частотные критерии устойчивости
- •1.8.3.1 Критерий Михайлова
- •1.8.3.2 Критерий Найквиста
- •1.8.3.3 Применение критерия Найквиста к системам с чистым запаздыванием
- •1.8.3.4 Логарифмический критерий Найквиста
- •1.8.4 Построение областей устойчивости сау
- •1.9 Оценка качества регулирования
- •1.9.1 Показатели точности сау
- •1.9.1.1 Типовые регуляторы
- •1.9.1.2 Определение показателей точности сау
- •1.9.2 Определение показателей качества переходных процессов
- •1.9.3 Определение показателей качества по корням характеристического уравнения
- •1.9.4 Интегральные показатели качества
- •1.9.5 Частотные показатели качества
- •1.10 Методы повышения точности сау
- •1.10.1 Повышение точности за счёт увеличения коэффициента передачи разомкнутой цепи
- •1.10.2 Повышение точности за счёт увеличения степени астатизма
- •1.10.3 Повышение точности за счёт введения в закон управления производной от ошибки или гибкой обратной связи
- •1.10.5 Повышение точности за счет применения неединичных ос
- •2 Цифровые системы управления
- •2.1 Функциональная схема сау и её циклограмма работы
- •2.2 Аналого-цифровые и цифро-аналоговые преобразователи
- •2.3 Понятие о решётчатых функциях и разностных уравнениях
- •2.4 Z-преобразование (дискретное преобразование Лапласа)
- •1) Свойство линейности.
- •2.5 Решение линейных разностных уравнений
- •2.6 Передаточные функции цифровых систем управления
- •2.7 Вычисление дискретной передаточной функции звена или группы звеньев по непрерывной передаточной функции
- •2.8 Системы с экстраполятором нулевого порядка
- •2.9 Передаточные функции замкнутых цифровых сау
- •2.10 Передаточные функции срп (регулятора). Формула Тастина
- •2.11 Частотные характеристики цифровых систем
- •2.12 Теорема Котельникова
- •2.13 Устойчивость движения цифровых сау
- •2.14 Порядок синтеза цифровых систем управления
- •3 Нелинейные системы автоматического управления
- •3.1 Основные нелинейные звенья
- •3.2 Структурные преобразования сау
- •Статические характеристики нелинейных систем.
- •3.3 Понятие о фазовом пространстве и фазовых траекториях
- •3.4 Особенности динамики нелинейных систем
- •3.5 Исследование устойчивости методами Ляпунова
- •3.5.1 Теорема Ляпунова об асимптотической устойчивости
- •3.5.2 Теорема Барбашина-Красовского
- •3.6 Исследование устойчивости методом фазовой плоскости
- •3.7 Критерий абсолютной устойчивости в.М. Пóпова
- •3.8 Гармоническая линеаризация
- •Идея гармонической линеаризации
- •Методика исследования предельных циклов с помощью метода гармбаланса
- •4 Элементы современной теории управления
- •4.1 Модальное управление
- •4.2 Запись дифференциальных уравнений в пространстве состояний
- •4.3 Описание работы двигателя постоянного тока (дпт) независимого возбуждения (нв) в пространстве состояний
- •4.4 Модальное управление в пространстве состояний
- •4.5 Динамические фильтры
- •4.6 Система управления с динамическими фильтрами
- •4.7 Редуцированные наблюдатели
- •4.8 Наблюдение объектов, подверженных действию возмущений и погрешностей датчиков (оценка внешних возмущений и погрешностей датчиков)
- •4.9 Использование наблюдателей для построения робастных систем управления
- •4.10 Асимптотическое дифференцирование с помощью наблюдателей
- •4.11 Заключение раздела 4
- •Литература
- •Приложение а Свойства комплексных функций
4.8 Наблюдение объектов, подверженных действию возмущений и погрешностей датчиков (оценка внешних возмущений и погрешностей датчиков)
На практике объекты управления всегда подвержены внешним воздействиям. Это нагрузка, ветер, трение и др. воздействия. В измерительных приборах часто присутствуют смещения нуля (постоянная погрешность), погрешности с частотой питающей сети и др. Во многих случаях законы изменения этих воздействий известны, но не известны их величины. В соответствии с этим объект управления описывается системой (1), (2)
![]() , (4.8.1)
, (4.8.1)
![]() , (4.8.2)
, (4.8.2)
где
![]() – векторы состояния, управления,
измерения, внешних воздействий и
погрешностей датчиков соответственно;
– векторы состояния, управления,
измерения, внешних воздействий и
погрешностей датчиков соответственно;
![]() – матрицы объекта, управления и
измерения.
– матрицы объекта, управления и
измерения.
Для решения
поставленной в названии подраздела
задачи надо внешние воздействия
![]() и погрешности датчиков
и погрешности датчиков![]() описать системой дифференциальных
уравнений.
описать системой дифференциальных
уравнений.
Например, пусть
![]() ,
тогда уравнение будет
,
тогда уравнение будет![]() .
.
Пусть теперь
![]() .
Введем обозначения
.
Введем обозначения![]() ,
,![]() .
Тогда
.
Тогда![]() и
и![]() .
.
Система уравнений
имеет вид
![]() или в матричной форме
или в матричной форме
 ,
,![]() ,
где
,
где![]() .
.
Пусть
![]() .
Введем обозначения
.
Введем обозначения![]() ,
,![]() .
Тогда система уравнений будет
.
Тогда система уравнений будет![]() ,
,![]() или
или
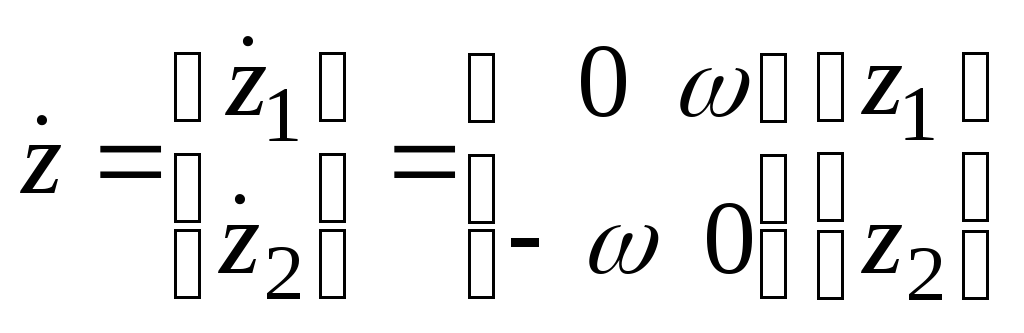 ,
,![]() ,
где
,
где![]() .
.
На основании сказанного можно записать
![]() ,
,![]() . (4.8.3)
. (4.8.3)
![]() ,
,![]() . (4.8.4)
. (4.8.4)
Таким образом, наряду с уравнениями (1) и (2), можно получить уравнения внешних воздействий на объект в виде
![]() (4.8.5)
(4.8.5)
Погрешности датчиков можно аналогичным образом описать в виде системы дифференциальных уравнений
![]() (4.8.6)
(4.8.6)
Для объединенной системы уравнений (1), (2) и (5), (6) расширенный вектор состояния примем в таком виде:
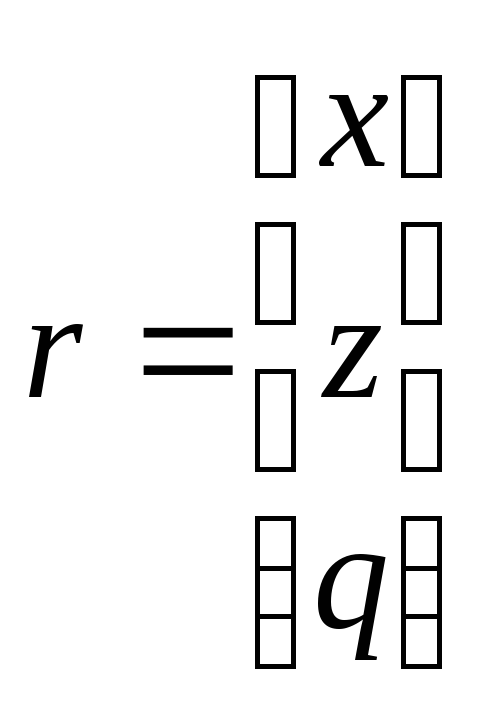 . (4.8.7)
. (4.8.7)
Тогда расширенная система (система с расширенным вектором состояния) будет выглядеть так:
 , (4.8.8)
, (4.8.8)
![]() . (4.8.9)
. (4.8.9)
Для оценки вектора
![]() наблюдатель, построенный по стандартному
принципу, имеет вид
наблюдатель, построенный по стандартному
принципу, имеет вид
![]() . (4.8.10)
. (4.8.10)
Для того чтобы
расширенный наблюдатель (10) был
работоспособен, необходимо и достаточно,
чтобы пара матриц (![]() )
была полностью наблюдаемой (чтобы
система уравнений (8), (9) была полностью
наблюдаемой). В результате решения
уравнения (10) существует оценка вектора
состояния
)
была полностью наблюдаемой (чтобы
система уравнений (8), (9) была полностью
наблюдаемой). В результате решения
уравнения (10) существует оценка вектора
состояния![]() ,
т.е. оценка
,
т.е. оценка![]() ,
,
![]() .
Таким образом, оцениваются вектор
состояния объекта управления, внешние
воздействия на него и погрешности
датчиков. В результате можно построить
закон управления в виде
.
Таким образом, оцениваются вектор
состояния объекта управления, внешние
воздействия на него и погрешности
датчиков. В результате можно построить
закон управления в виде
![]() . (4.8.11)
. (4.8.11)
Подставим (11) в (1). Получим
![]() . (4.8.12)
. (4.8.12)
Если
![]() ,
то внешнее воздействие будет
скомпенсировано. Как известно, такой
принцип управления называетсякомбинированным
управлением.
,
то внешнее воздействие будет
скомпенсировано. Как известно, такой
принцип управления называетсякомбинированным
управлением.
4.9 Использование наблюдателей для построения робастных систем управления
Пусть задан объект управления в виде
![]() (4.9.1)
(4.9.1)
с измерением
![]() . (4.9.2)
. (4.9.2)
Система (1), (2) совпадает с системой (4.8.1), (4.8.2), для которой в подразделе 4.8 даны принятые обозначения. На практике параметры системы управления (СУ), во-первых, точно не известны, во-вторых, они могут существенно изменяться как в процессе хранения, так и в процессе эксплуатации. В частности, в электроприводе существенно неопределенными могут быть приведенный момент инерции ротора и сопротивления ротора и статора. Эти параметры могут меняться в два раза как вверх, так и вниз. Такие большие изменения параметров делают обычные классические СУ неработоспособными. Для обеспечения работоспособности в условиях сильной неопределенности разработаны специальные СУ. Это адаптивные СУ, СУ с переменной структурой (СПС) (системы со скользящими режимами) и др.
Системы управления, работоспособные в условиях большой неопределенности, получили название робастных СУ (от английского robust – жесткий, прочный). В данном подразделе будет рассматриваться комбинированная СУ с наблюдателем неопределенности, аналогичная системе, изученной в подразделе 4.8.
Будем полагать, что
![]() , (4.9.3)
, (4.9.3)
где
![]() – номинальные матрицы, элементы которых
обычно известны из паспортных данных,
– номинальные матрицы, элементы которых
обычно известны из паспортных данных,
![]() – неизвестные отклонения от номинальных
значений.
– неизвестные отклонения от номинальных
значений.
Подстановка (3) в (1) и (2) дает
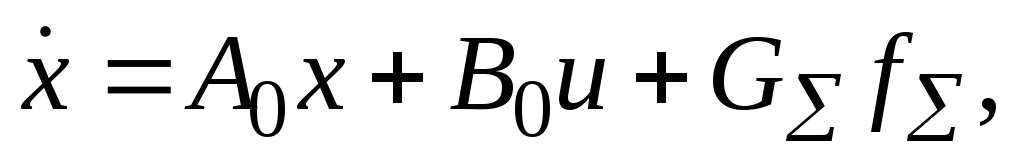 (4.9.4)
(4.9.4)
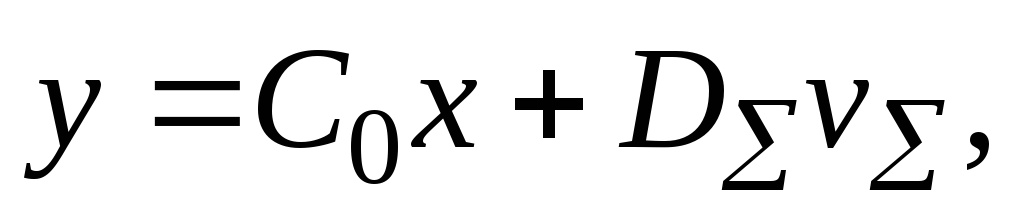 (4.9.5)
(4.9.5)
где
![]() – (4.9.6)
– (4.9.6)
векторы неопределенностей. Уравнения (4), (5) по структуре полностью соответствуют уравнениям (4.8.1), (4.8.2).
Ставится задача:
для системы (4), (5) синтезировать
наблюдатель, оценивающий вектор
![]() и векторы неопределенностей. Как видно
из (6), векторы неопределенностей меняются
со скоростями того же порядка, что и
векторы
и векторы неопределенностей. Как видно
из (6), векторы неопределенностей меняются
со скоростями того же порядка, что и
векторы![]() и
и![]() .
Поэтому быстродействие наблюдателя
назначим таким, что за время переходного
процесса наблюдателя переменные
.
Поэтому быстродействие наблюдателя
назначим таким, что за время переходного
процесса наблюдателя переменные![]() и
и![]() изменяются настолько мало, что на этом
интервале времени можно полагать
изменяются настолько мало, что на этом
интервале времени можно полагать ,
, или
или
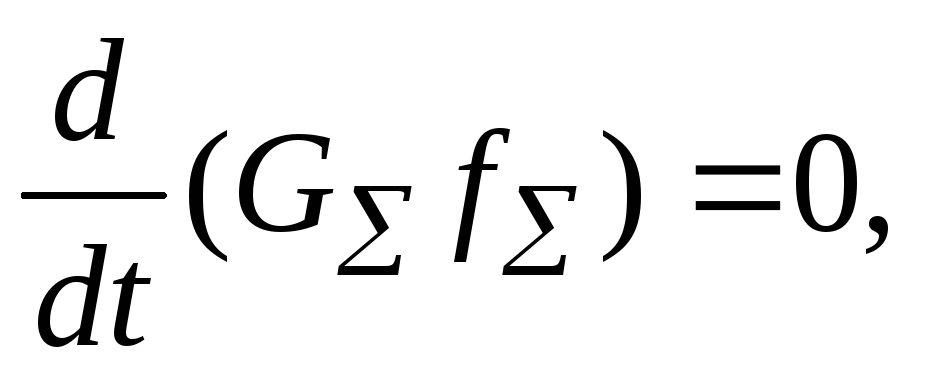
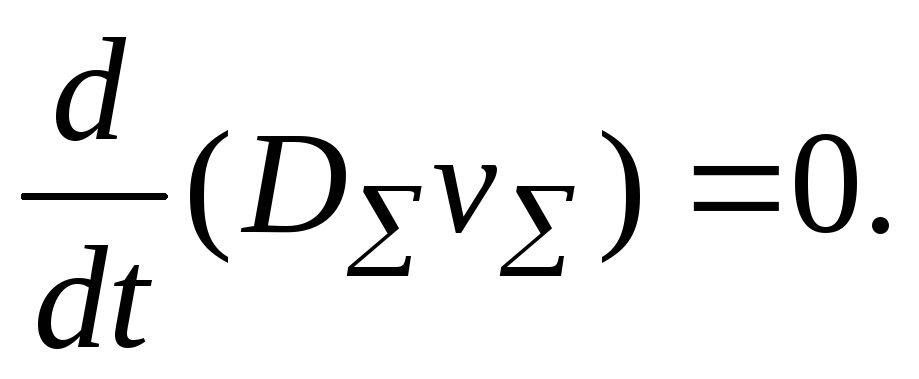 (4.9.7)
(4.9.7)
Если система (4),
(5), (7) является полностью наблюдаемой,
то по методике, изученной в подразделе
4.8, можно построить наблюдатель,
оценивающий вектор состояния и векторы
неопределенностей без погрешностей,
вносимых последними. По информации,
полученной с помощью наблюдателя, можно
задать комбинированный закон управления
типа (4.8.11), с помощью которого парируется
влияние вектора неопределенности
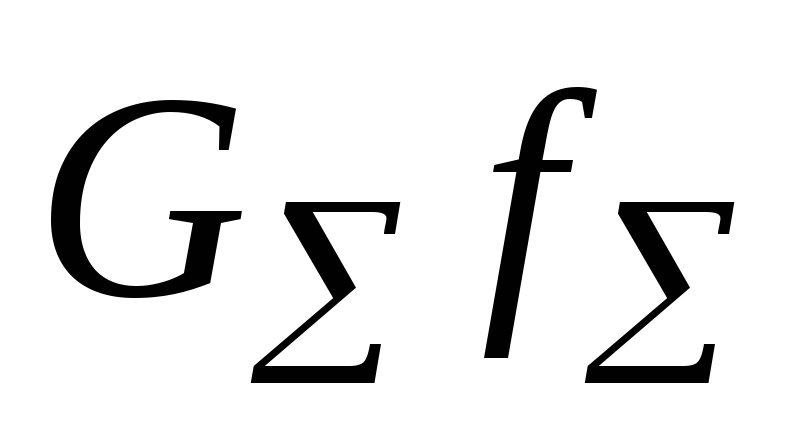 .
.
