1.8.3.3 Применение критерия Найквиста к системам с чистым запаздыванием

Рассмотрим структурную схему САУ, представленную на рис. 13,

Рисунок 1.8.13

где – передаточная функция разомкнутой системы без учёта чистого запаздывания;

–передаточная функция чистого запаздывания (– величина чистого запаздывания).

На рис. 14 продемонстрировано соотношение между входным () и выходнымсигналами звена чистого запаздывания.

Рисунок 1.8.14

Пусть система без учёта чистого запаздывания является асимптотически устойчивой с годографом Найквиста, представленным на рис. 15.

Задача: найти значение чистого запаздывания, при котором система выходит на границу устойчивости. Это значение называется критическим запаздыванием .

Передаточная функция разомкнутой САУ

,

Рисунок 1.8.15

АФЧХ разомкнутой системы

. (1.8.3.10)

На основании (10) можно заключить, что АЧХ в системах без учёта чистого запаздывания и с учётом чистого запаздывания совпадают, а ФЧХ полной системы имеет сдвиг по фазе на величину -по отношению к идеальной системе. Очевидно, что при возрастании угол поворота увеличивается. Пусть система без запаздывания асимптотически устойчива и в разомкнутом, и в замкнутом состояниях. Это означает, что АФЧХ не охватывает точку (-1; j0). Будем увеличивать запаздывание от значения, равного нулю, и следить за деформацией годографа. Пригодограф пройдет через точку (-1; j0) и, следовательно, система окажется на границе устойчивости. Данная ситуация отражена на рис. 15. На рисунке 1 – АФЧХ ,2 – окружность единичного радиуса, – точка пересечения кривойс окружностью 2. Поскольку в этой точке, то в этой точке. Подчеркнем, что частоты среза в системах с чистым запаздыванием и без него совпадают. На основании рис. 15 можно записать. Угол можно замерить на рис. 15, тогда

. (1.8.3.11)

1.8.3.4 Логарифмический критерий Найквиста

Это тот же критерий Найквиста, но сформулированный на языке логарифмических характеристик. Для удобства рассмотрим специфическое взаимное расположение ЛАЧХ и ЛФЧХ, где угол ЛФЧХ расположен на горизонтали, соответствующей 0 дБ, а положительная полуось ЛФЧХ направлена вниз. Описанная ситуация отражена на рис. 16.

Рисунок 1.8.16

Критерий. Для того чтобы замкнутая система была асимптотически устойчивой, необходимо и достаточно, чтобы при заданном взаимном расположении систем координат ЛАЧХ и ЛФЧХ и при изменении частоты от 0 до бесконечности ЛФЧХ огибала точку среза снизу (кривая 1).

Для того чтобы замкнутая САУ находилась на границе устойчивости, ЛФЧХ должна проходить через точку среза (кривая 2).

Для того чтобы замкнутая САУ была неустойчивой, достаточно, чтобы ЛФЧХ огибала точку среза сверху (кривая 3).

Содержание рис. 16 называется диаграммой Боде. По этой диаграмме и выражению (11) можно найти критическое запаздывание.

1.8.4 Построение областей устойчивости сау

При синтезе САУ, когда требуется определить влияние каких-либо варьируемых параметров на устойчивость, строят области устойчивости в пространстве этих параметров.

Области устойчивости – это совокупность значений параметров системы, при которых система асимптотически устойчива.

При двух варьируемых параметрах это области на плоскости, при трёх – в трёхмерном пространстве. Если в пространстве всех своих параметров система не имеет области устойчивости, то она называется структурно неустойчивой. Построение границ областей устойчивости осуществляется с помощью критериев устойчивости. Для этой цели наиболее часто используется критерий Михайлова.

Область устойчивости, построенная по критерию Михайлова, называется D-областью, а метод построения областей устойчивости по критерию Михайлова называется D-разбиением.

Для применения метода D-разбиения необходимо иметь характеристическое уравнение

. (1.8.4.1)

Различают три типа границ областей устойчивости:

1) апериодическая,

2) граница с бесконечно большим корнем,

3) колебательная.

Пусть требуется построить области устойчивости на плоскости варьируемых параметров и, т.е. коэффициенты характеристического уравнения зависят от этих параметров.

,

где n – показатель степени характеристического уравнения.

Для получения апериодической границы полагают

. (1.8.4.2)

Уравнение (2) есть уравнение кривой 1 на плоскости (рис. 17).

Рисунок 1.8.17

Для получения границы с бесконечно большим корнем полагают

. (1.8.4.3)

Уравнение (3) есть уравнение кривой 2 на рисунке.

Из характеристического уравнения (1)

.

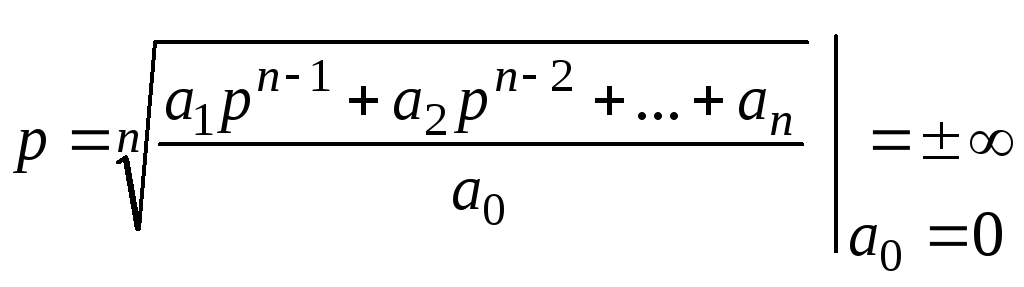Поэтому уравнение (3) называют границей с бесконечно большим корнем.

Для получения колебательной границы в уравнении (1) делают подстановку , где– мнимая единица,– частота. В результате получается характеристический комплекс

. (1.8.4.4)

Комплексная переменная тогда и только тогда равна 0, когда одновременно равны нулю её действительная и мнимая части, т.е.

. (1.8.4.5)

Система (5) представляет собой уравнение кривой 3 на плоскости , заданной в параметрическом виде, где роль параметра выполняет.

В результате плоскость оказалась разбитой на 7 областей.

Существует несколько методов выделения областей устойчивости:

1. метод штриховки;

2. применение критериев устойчивости;

3. метод проб.

При применении метода проб в исследуемой области назначают точку с определёнными значениями . При этих значениях находят значения коэффициентов характеристического уравнения, а затем с помощью любого критерия, использующего характеристическое уравнение, определяется устойчивость системы в данной точке. Если система асимптотически устойчива (неустойчива) в данной точке, то она асимптотически устойчива (неустойчива) во всей исследуемой области. В качестве примера рассмотрим задачу.

Задача: построить область устойчивости системы, представленной на рис. 18, на плоскости параметров , где У – усилитель, ЭД – электродвигатель.

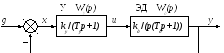
Рисунок 1.8.18 – Структурная схема электропривода

На рисунке представлена структурная схема электропривода (ЭП), регулирующего угол поворота , с обозначениями

–коэффициенты передачи,

–постоянные времени.

Передаточная функция разомкнутой системы

. (1.8.4.6)

Передаточная функция замкнутой системы

. (1.8.4.7)

Для получения характеристического уравнения приравниваем знаменатель в (7) к нулю.

.

Приведём к общему знаменателю

.

Дробь равна 0, когда числитель равен нулю, т.е.

.

Это характеристическое уравнение замкнутой САУ приведём к стандартному виду

, (1.8.4.8)

где

.

Построим область устойчивости.

Апериодическая граница устойчивости

. (1.8.4.9)

Граница с бесконечно большим корнем

. (1.8.4.10)

Колебательная граница устойчивости в соответствии с (5) и (8) определяется системой

(1.8.4.11)

Из второго уравнения системы (11) следует:

(1.8.4.12)

Подстановка в первое уравнение в (11) дает. Это уже найденная апериодическая граница устойчивости (9). Из (12) найдёми подставим в первое уравнение системы (11). Тогда

. (1.8.4.13)

Это уравнение колебательной границы устойчивости.

Границы областей (9), (10), (13) изображены на рис. 19.

Найдем среди пяти областей область устойчивости. Для этого воспользуемся коэффициентными критериями устойчивости.

Рисунок 1.8.19

Необходимые условия асимптотической устойчивости (положительность всех коэффициентов характеристического уравнения) дают

.

Примечание: неравенство над стрелкой указывает на то, что преобразование осуществлено с использованием этого неравенства.

Таким образом, областями устойчивости могут быть вторая и третья области. Для окончательного выявления области устойчивости воспользуемся критерием Раусса-Гурвица применительно к системе третьего порядка. Этот критерий дает

,

отсюда следует

. (1.8.4.14)

Граница области устойчивости дана в (13). Тогда из уравнения (14) следует, что областью устойчивости является область II.