Методика исследования предельных циклов с помощью метода гармбаланса

1. Предполагается, что условие фильтра выполняется.

2. Осуществляется гармоническая линеаризация, в результате которой нелинейная система заменяется линейной системой.

3. Предельным циклам в нелинейной системе соответствует граница устойчивости в эквивалентной линейной системе.

4. С помощью любого критерия устойчивости для линейных систем находятся значения её параметров, при которых система находится на границе устойчивости.

5. С помощью этих параметров находятся коэффициенты гармонической линеаризации, амплитуда и частота предельных циклов.

6. Зная амплитуду и частоту предельных циклов, с помощью АЧХ линейной части системы проверяется выполнение условия фильтра.

7. При выполнении условия фильтра предельные циклы исследуются на устойчивость.

8. Зная характер устойчивости предельных циклов, можно определить направление развития фазовых траекторий. К устойчивым предельным циклам фазовые траектории притягиваются. В этом случае возникнут автоколебания. Неустойчивые предельные циклы фазовые траектории могут пересекать.

4 Элементы современной теории управления

То, что изучалось выше, входит в классическую теорию управления, которая обычно излагается на языке передаточных функций с использованием частотных свойств САУ.

Современная теория управления базируется на описании системы управления в пространстве состояний, т.е. система уравнений приводится к форме Коши, вводится вектор состояния, составленный из координат, характеризующих состояние системы управления, и в соответствии с вектором состояния составляются матрицы коэффициентов системы управления. В этом случае можно применить хорошо разработанные методы решения и исследования систем дифференциальных уравнений.

4.1 Модальное управление

См. раздел «Корневые критерии устойчивости».

Решение дифференциальных уравнений или системы дифференциальных уравнений можно представить в виде

, (4.1.1)

где – простые корни характеристического уравнения, – постоянные интегрирования. Каждое слагаемое в выражении (1) называетсямодой. Поведение всей системы зависит от поведения каждой моды. Поэтому, задавая значения корней характеристического уравнения в каждой моде, можно сформировать любой переходный процесс. Заданию корней соответствует их размещение на комплексной плоскости. Помещение всех корней замкнутой САУ в любое наперёд заданное положение составляет предмет модального управления.

Рассмотрим дифференциальное уравнение n-го порядка

, (4.1.2)

где – единичная ступенчатая функция,– постоянные коэффициенты.

Характеристическое уравнение имеет вид

. (4.1.3)

Уравнение (3) можно представить в виде

, (4.1.4)

где – корни характеристического уравнения.

Было изучено большое количество распределений корней характеристического уравнения и сформированы так называемые стандартные характеристические уравнения, которые обеспечивают тот или иной заданный переходный процесс.

Наиболее простым распределением является биномиальное распределение корней. При этом распределении

.

В этом случае характеристическое уравнение в соответствии с (4) принимает вид

, (4.1.5)

а корни могут быть только действительными и равными. Обычно полагают

, (4.1.6)

где – характерная частота, определяющая быстродействие системы.

Характеристические полиномы различных порядков при биномиальном распределении корней и при , полученные по выражениям (5) и (6), приведены в (7)

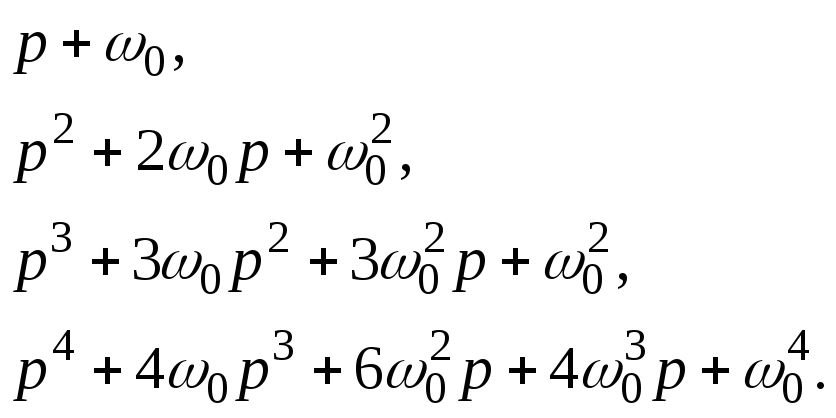(4.1.7)

Для этого случая переходные процессы при различных порядках системы представлены на рис. 1, где цифры 1, 2, 3,… указывают на порядок системы. Все процессы построены для одного и того же значения . Биномиальное распределение корней даёт апериодический процесс (без перерегулирования). Такой процесс необходим, например, при автоматизированной сборке.

Другим распространённым распределением корней является распределение корней по Баттерворту. При этом стандартные характеристические полиномы имеют следующий вид:

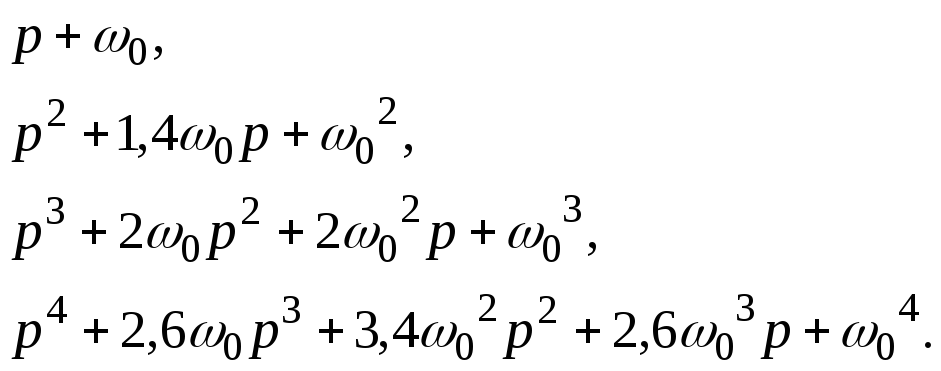(4.1.8)

При распределении корней по Баттерворту реакции на единичное ступенчатое воздействие представлены на рис. 2.

Рисунок 4.1.1 – Типовые переходные процессы при биномиальном распределении корней

Рисунок 4.1.2 – Типовые переходные процессы при распределении корней по Баттерворту

При этом распределении корни расположены на полуокружности радиуса , деля ее на равные отрезки (рис. 3-5).

При синтезе системы управления следует пользоваться рис. 1, 2 следующим образом.

Предположим, что система четвертого порядка и переходный процесс должен закончиться через время . Тогда в соответствии с рис. 2 можно записать

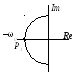
Рисунок 4.1.3

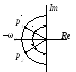
Рисунок 4.1.4

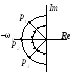
Рисунок 4.1.5

.

Таким образом, становится известным желаемое характеристическое уравнение. Синтез САУ с помощью модального управления осуществляется следующим образом:

1. составляется характеристическое уравнение системы, в котором неизвестные параметры заданы буквенно;

2. по графику определяется ;

3. полученное характеристическое уравнение системы сравнивается со стандартным уравнением того же порядка, в результате чего получается система уравнений относительно неизвестных параметров системы;

4. находятся неизвестные параметры.