2.4 Z-преобразование (дискретное преобразование Лапласа)

Выше разностные уравнения были получены из дифференциальных уравнений приближённым методом с помощью конечных разностей. Для получения точных разностных уравнений используется z-преобразование или дискретное преобразование Лапласа. Если для непрерывных систем используется обычное преобразование Лапласа

, (2.4.1)

то дискретное преобразование Лапласа в безразмерном времени имеет вид

. (2.4.2)

В размерном времени

. (2.4.3)

Функция называетсяоригиналом, а – еёz-отображением, –символ преобразования.

С помощью z-преобразования разностные уравнения приводятся к алгебраическим уравнениям, которые решаются гораздо легче, чем разностные, а затем к полученным решениям применяют обратное z-преобразование, которое обозначается так:

, (2.4.4)

в результате чего получаем разностные уравнения.

Найдём z-преобразования простейших функций времени.

1) единичная ступенчатая функция

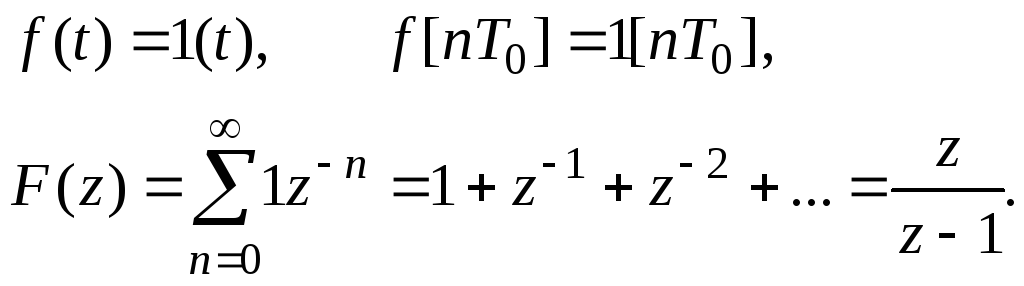
Последнее выражение представляет собой геометрическую прогрессию.

2) линейная функция времени

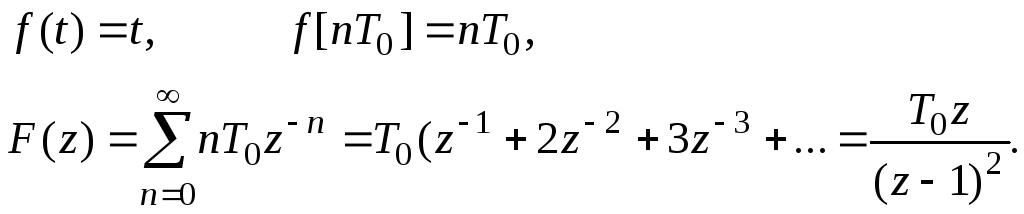
Аналогичным образом можно найти z-отображения и других функций времени.

Для решения разностных уравнений надо находить z-отображения не только для функций времени, стоящих в правой части уравнения, а и для искомых функций, которые обычно записываются в левой части разностного уравнения.

Для их преобразования используют ряд свойств. Рассмотрим некоторые из них.

Некоторые основные свойства z-преобразования.

1) Свойство линейности.

. (2.4.5)

2) теорема сдвига.

Если временное запаздывание равно целому числутактов счёта, то

формула сдвига вправо

, (2.4.6)

формула сдвига влево

. (2.4.7)

3) изображение прямых и обратных разностей.

(2.4.8)

(2.4.9)

4) теорема о начальном и конечном значении оригинала.

, (2.4.10)

. (2.4.11)

5) теорема свёртки.

, (2.4.12)

где

. (2.4.13)

6) обратное z-преобразование.

Обратное z-преобразование позволяет найти оригинал по егоz-отображению . Это преобразование обозначается так:

. (2.4.14)

Существует несколько методов обратного z-преобразования:

а) метод неопределённых коэффициентов.

Пусть найдено в виде

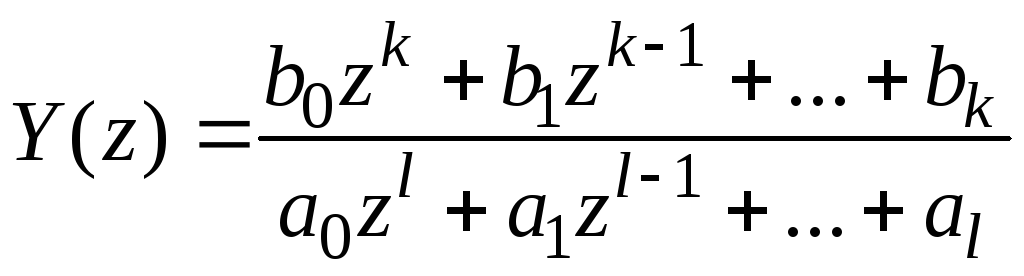. (2.4.15)

Пусть знаменатель в (15) имеет простых корней , тогда его можно представить в виде

, (2.4.16)

т.е. выражение (15) можно представить в виде

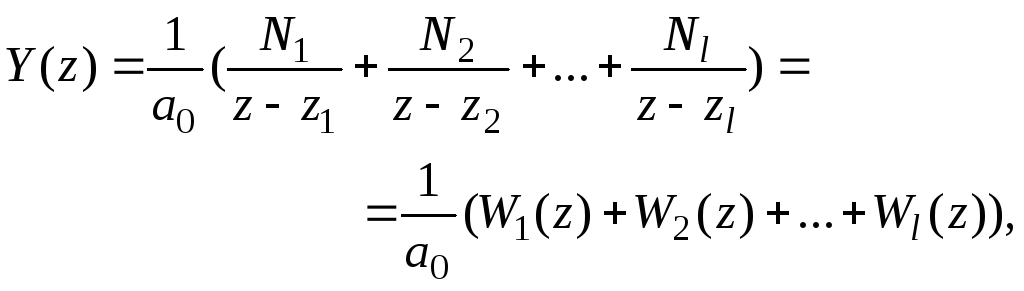(2.4.17)

где – неопределённые коэффициенты. Эти коэффициенты определяются следующим образом. Выражение (17) приводится к общему знаменателю. Затем выражения (15) и (17) приравниваются друг другу. В полученном выражении приравниваются числители. В полученном равенстве приравниваются коэффициенты при одинаковых степенях. Из полученной системы уравнений находятся неизвестные коэффициенты. В результате вместо сложного выражения (15) получается выражение (17), состоящее из суммы элементарных функций.

б) с использованием ряда Лорана.

Решение алгебраического уравнения, полученного с помощью z-преобразования, можно представить в виде

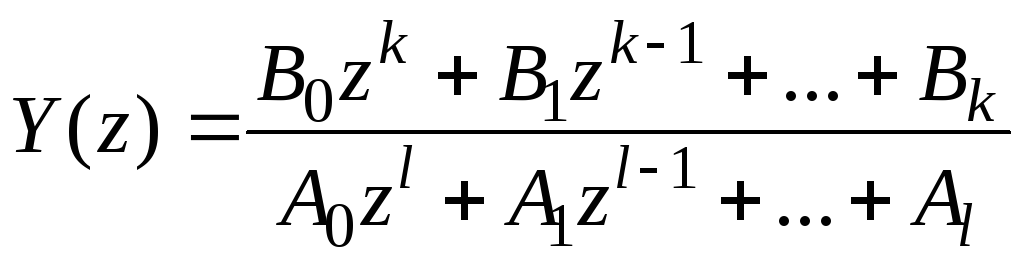. (2.4.18)

Будем отыскивать разложение этого выражения в виде ряда Лорана

, (2.4.19)

где – неизвестные коэффициенты. Для нахожденияприравняем выражения (18) и (19), приведём полученное равенство к общему знаменателю и в числителях правых и левых частей приравняем коэффициенты при одинаковых степенях. В результате получим систему алгебраических уравнений для определения неизвестных коэффициентов. Сравнивая выражение (19) с выражениемz-преобразования (20)

, (2.4.20)

получим или .являются значениями искомой функции в различные моменты времени.