3.5 Исследование устойчивости методами Ляпунова

Методы исследования устойчивости Ляпунова позволяют исследовать устойчивость систем управления, описываемых линейными, нелинейными, дискретными, непрерывными, бесконечномерными уравнениями, а также уравнениями в частных производных.

Достоинство этого метода заключается в том, что для исследования устойчивости не требуется находить ни решения дифференциальных уравнений, ни рассчитывать корни.

Физическая суть методов Ляпунова. На рисунке 1 представлена фазовая траектория асимптотически устойчивой САУ. Стрелками указаны различные положения радиус-вектора .

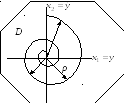
Рисунок 3.5.1 – Фазовый портрет асимптотически устойчивой траектории

Радиус-вектор изображающей точки на рис. 1 определяется выражением

.

Условием асимптотической устойчивости являются условия

, или .

Для системы третьего порядка .

Для системы n-го порядка .

Помимо перечисленных функций об асимптотической устойчивости можно судить и по другим функциям, например, для системы 2-го порядка

.

Или другая четная функция

.

Функция , с помощью которой удаётся судить об устойчивости системы, называетсяфункцией Ляпунова.

Для функции Ляпунова характерно то, что она является всегда положительной и обращается в 0 только в начале координат.

Функция , зависящая от всех координат вектора состояния, называетсяопределённо положительной (отрицательной) в области , содержащей начало координат, если в этой области она везде положительна (отрицательна) кроме начала координат, где она обращается в ноль.

Функция называетсязнакоположительной (знакоотрицательной), если она в этой области удовлетворяет соотношению .

Признаками асимптотической устойчивости системы являются: существование для исследуемых уравнений определённо положительной функции и в любой момент времени, т.е. должна быть определённо отрицательной.

3.5.1 Теорема Ляпунова об асимптотической устойчивости

Рассмотрим систему нелинейных дифференциальных уравнений

. (3.5.1.1)

–в общем случае нелинейные функции.

Теорема Ляпунова. Если для системы (1) в области , содержащей начало координат, существует определённо положительная функция , полная производная которой по времени , взятая в силу системы (1), будет определённо отрицательной, то начало координат будет асимптотически устойчивым при условии, что начальные условия взяты из области .

Пусть для системы (1) существует функция Ляпунова

. (3.5.1.2)

Фраза “полная производная по времени, взятая в силу системы (1)” означает следующее:

. (3.5.1.3)

Пример. Пусть дана система нелинейных уравнений

(3.5.1.4)

Выберем в качестве функции Ляпунова функцию

, (3.5.1.5)

где

. (3.5.1.6)

В соответствии с (3) получим полную производную по времени.

Примечание: цифра над равенством указывает на то, что преобразование осуществлено с использованием формулы (4).

При выполнении условий (6) и

(3.5.1.7)

функция (определенно отрицательна).

Таким образом, при выполнении условий (6) и (7) начало координат системы (4) будет асимптотически устойчивым при любых начальных условиях, т.е. будет иметь место асимптотическая устойчивость в целом (глобальная устойчивость). Теорема Ляпунова дает достаточные условия асимптотической устойчивости.