14.1.3 Теорема о циркуляции вектора . Примеры применения теоремы

Расчёт сил, действующих в магнитном поле на проводники с током и движущиеся заряды, требует умения вычислять значение индукции магнитного поля в любой точке пространства. Это можно сделать, используя закон Био-Савара-Лапласа, однако, в ряде случаев, для расчётов удобно применять другой подход, основанный на использовании теоремы о циркуляции вектора . Данный подход во многом схож с тем, который лежит в основе вычисления напряженности электрического поля путём применения теоремы Гаусса.

Для начала введём определение.

Если в пространстве, каждой точке которого соответствует некоторый вектор , выбрать замкнутый контур L и затем начать обходить этот контур в каком-то направлении, то каждому малому элементу длины этого контура (направление вектора совпадает с направлением обхода) можно сопоставить скалярное произведение ()  Adlcos, где A – величина вектора в области выбранного вектора , а  – угол между этими векторами. Просуммировав такие произведения вдоль всего контура, мы получаем интеграл (обозначим его буквой ), который называется циркуляцией вектора по контуру L:

  . (14.4)

После того, как мы записали определение циркуляции вектора¹, сформулируем теорему, вынесенную в заглавие параграфа.

Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна умноженной на магнитную постоянную ₀ алгебраической сумме токов, которые пронизывают поверхность, мысленно натянутую на этот контур:

 ₀. (14.5)

При вычислении суммы следует учитывать направление обхода контура: те токи, которые пронизывают поверхность, мысленно натянутую на контур в направлении, совпадающем с направлением хода винта (буравчика), вращаемого в сторону обхода, берутся со знаком «плюс», те, которые идут в противоположном направлении, – со знаком «минус».

Точно так же, как и в случае теоремы Гаусса для электрического поля, в которой речь шла о произвольной замкнутой поверхности, выбираемый контур обхода может иметь любую форму, и именно поэтому его выбирают таким, чтобы можно было легко взять интеграл и, тем самым, получить формулу для расчёта индукции B в заданной точке пространства.

Рассмотрим два примера.

а) Расчёт индукции магнитного поля прямого бесконечно длинного тонкого проводника с током

Выполним шаги, аналогичные тем, которые мы делали в случае использования теоремы Гаусса для электрического поля.

– Начертим рисунок с изображением проводника с током и силовых линий создаваемого им магнитного поля (рис. 14.4).

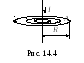– Укажем на рисунке точку, в которой мы будем рассчитывать величину индукции магнитного поля, и проведём сквозь эту точку силовую линию (на рис. 14.4. это точка А).

– Выберем замкнутый контур, форма которого соответствовала бы симметрии задачи; контур должен проходить через нужную нам точку А (на рис. 14.4. это окружность радиусом R, плоскость которой перпендикулярна проводнику с током, проходящему через центр этой окружности).

– Посчитаем циркуляцию вектора индукции магнитного поля по выбранному контуру. Обход совершим по направлению силовых линий, тогда в формуле (14.5) ток можно будет брать со знаком «плюс».

Во всех точках выбранный нами контур совпадает с одной и той же силовой линией и согласуется с ней по направлению обхода, поэтому угол  между векторами и везде равен нулю. Кроме того, в силу симметрии контура (все участки которого находятся на равном расстоянии от проводника с током) во всех его точках величина индукции одинакова, и множитель B можно вынести за знак интеграла. Учтём также, что, по определению интеграла,  2R. Сказанное означает:

   B  2RB.

– Определим теперь, какой суммарный ток пронизывает поверхность, мысленно натянутую на выбранный контур, после чего применить теорему о циркуляции вектора .

В нашем случае речь идёт только об одном токе I, следовательно, циркуляция вектора должна просто равняться произведению ₀I, то есть,

2RB  ₀I.

Сказанное означает, что индукция магнитного поля, создаваемого прямым тонким бесконечно длинным проводником с током I на расстоянии R от него, рассчитывается по формуле:

B  . (14.6)

б) Расчёт индукции магнитного поля тороида (и бесконечно длинного соленоида) с током

Тороид представляет собой тороидальный (имеющий «форму бублика») сердечник, изготовленный из немагнитного материала, на который виток к витку плотно навит провод в тонкой изоляционной оболочке. На рис. 14.5.а) показан вид такого объекта сверху; для того, чтобы не загромождать чертёж, витки провода изображены лишь в его левой части. Заметим: тороидом бесконечно большого радиуса R можно считать бесконечно длинный соленоид.

Всё пространство вокруг проводов с током I, идущим по тороиду, можно разбить на три области. Область I соответствует точкам, лежащим вне тороида, область II – точкам, которые находятся в его «дырке» и область III, лежащая в «теле» сердечника тороида (рис. 14.5.б). Определим, какова индукция магнитного поля в этих областях на примере точек A, A и A.

Проведём через точку A замкнутый контур I, окружающий тороид. Поверхность, мысленно натянутая на тот контур, пересекается каждым витком дважды (рис. 14.5.в), поэтому алгебраическая сумма токов, идущих по виткам и пронизывающих эту поверхность равна нулю, какой бы формы контур мы ни выбирали. Но если при любом выборе формы контура интеграл по нему равен нулю, то это означает, что под знаком интеграла также стоит ноль. Так как явно не ноль, это означает, что вне тороида индукция магнитного поля равна нулю, то есть вне тороида магн итного поля нет.

Аналогичная ситуация имеет место и в области II. Какой бы формы контур (овальный, треугольный, четырёхугольный и т. д.), проходящий через точку A мы ни выбирали, циркуляция вектора по нему будет равна нулю, так как поверхности, натянутые на каждый из этих контуров токами вообще не пересекаются. И снова, - если для любого контура интеграл равен нулю, следовательно, дело в подынтегральном выражении – оно (точнее вектор ) тождественно равно нулю: магнитного поля нет и в области II.

Но в области III ситуация качественно иная: поверхность, натянутая на контур - окружность, которая совпадает со средней линией тороида, пронизывается каждым витком только один раз, и все соответствующие токи идут в одном направлении. Ранее силовые линии внутри соленоида мы уже рисовали; с учётом того, что и внутри тороида силовые линии на каждом участке параллельны контуру обхода – окружности, можно записать, что угол  между и в любом месте равен нулю. Кроме того, в силу симметрии контура и тороида, индукция B должна быть одинакова в любой точке контура, длина которого равна 2R:

   B  2RB.

Сумма токов, пронизывающих поверхность, мысленно натянутую на выбранный контур, равна NI, где N – общее число витков проволоки. Сказанное означает: внутри тороида (так же, как и внутри бесконечно длинного соленоида)

B  ₀I  ₀nI, (14.7)

где n – число витков на единицу длины тороида.

Формулы (14.6) и (14.7) совпадают с формулами, которые можно получить для этих же объектов, используя закон Био-Савара-Лапласа (см. предыдущую лекцию).