Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4603 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Киевский национальный университет строительства и архитектуры
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
M.L.Zocenko_-_Inzh_geol_Mehan_gruntiv_osnovy_i_fund.pdf
Скачиваний:
663
Добавлен:
05.02.2016
Размер:
6.57 Mб
Скачать
☆
►Содержание►

10. ЗАСТОСУВАННЯ ТЕОРІЇ НЕЛІНІЙНОГО ДЕФОРМУВАННЯ ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ МЕХАНІКИ ҐРУНТІВ

10.1. СУЧАСНІ УЯВЛЕННЯ ПРО НЕЛІНІЙНУ ДЕФОРМАТИВНІСТЬ ҐРУНТІВ

Основи широкого кола споруд у складних інженерно-геологічних умовах (див. розділ 16), великомасштабних будівель із значними навантаженнями на несучі конструкції та фундаменти, об’єктів у аварійному й передаварійному стані тощо досить часто працюють за межею лінійного деформування. У ряді ж випадків і для досить традиційних рішень системи “основа – фундаменти – будівля” величина її деформацій, одержана при застосуванні теорії лінійного деформування (див. розділ 7), виявляється значно меншою за їх допустимі значення. Але запроектувати більші навантаження, згідно з положеннями лінійної механіки ґрунтів, неможливо, адже при підвищенні навантаження порушується прийнята в розрахунках лінійна залежність між напругами й деформаціями.

На рис. 10.1 представлена структурна схема (за професором Д. М. Шапіро, 1996), яка узагальнює основні види нелінійності, що зустрічаються при проектуванні будівельних об’єктів, і яка охоплює більшість практично важливих задач та технічних теорій.

Фізична нелінійність матеріалів і ґрунтів проявляється як відхилення від закону Гука співвідношень між деформаціями ε й діючими напругами σ. Це явище становить різні форми розвитку пластичних деформацій: текучість – швидкоплинне деформування при постійних напругах; повзучість – прогресування пластичних деформацій у часі; криволінійна діаграма зв’язку міжε та σ, притаманна матеріалам (середовищам) із змінним (залежним від напруг)

 

 

 

 

 

Основні види нелінійності

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

фізична

 

 

 

 

 

 

 

геометрична

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

текучість

 

 

 

 

 

 

 

 

 

 

 

 

 

переміщення

 

 

однобічні

 

 

зрушення

 

 

поздовж-

 

в суцільних

повзучість

 

 

 

 

 

 

 

 

 

 

зв’язки:

 

за заданою

 

 

ній

 

тілах, сумірні

 

 

 

 

 

 

 

 

криволінійна

 

нездатність до

 

(розрахун-

 

 

вигин,

 

з розмірами

діаграма

 

сприйняття

 

 

ковою)

 

 

втрата

 

конструкцій

зв’язку між

 

розтягнення

 

поверхнею

 

 

стійкості

 

(кінцевих

напругами та

 

(стиснення)

 

 

 

 

 

 

 

 

 

елементів)

деформаціями

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 10.1. Основні види нелінійності основ і будівельних конструкцій

модулем деформації чи із зміцненням, тобто здатністю сприймати зростаюче навантаження при збільшенні пластичної складової деформацій. Нагадаємо, що характерна схема розвитку деформацій ґрунтового масиву від дії на штамп (фундамент) зростаючого навантаження подана на рис. 6.1, а типові графіки залежності ε=f(σ) найбільш поширених моделей ґрунту – на рис. 6.11. Зазначимо також, що на порушення лінійної залежності між напругами і деформаціями певною мірою впливають дилатансія та анізотропія ґрунтів, їх реологічні й динамічні властивості (є сенс коротко переглянути п.п. 4.9-4.12).

229

Іншим різновидом фізичної нелінійності є однобічні зв’язки, тобто безперешкодний розвиток деформацій одного знаку (стиснення-розтягнення) та збереження несучої здатності при сприйманні нормальних напруг іншого напрямку. Прикладами конструкцій, що сприймають лише стиснення, можуть бути контактні поверхні під плитою фундаментів, бічні поверхні паль, які відокремлюються при вигині від ґрунтової основи, матеріал навколо тріщин тощо. Лише на розтягнення працюють конструкції типу вант, струн, затяжок. Іноді однобічні зв’язки ще відносять до конструктивної нелінійності.

Ще один вид фізичної нелінійності, характерний саме для ґрунтів, – зрушення (сковзання) за деякою поверхнею, котра або визначається розрахунком, або умовами геотехнічної задачі (наприклад, площина контакту підошви фундаменту та ґрунтової основи, межа геологічних нашарувань, поверхня ковзання ґрунтового укосу тощо).

Геометрична нелінійність звичайно проявляється у поздовжньому вигині центрально- і позацентрово стиснутих стрижнів (наприклад, паль) через ексцентриситет дії поздовжньої сили, що виникає при відхиленні від положення рівноваги.

Іншою формою геометричної нелінійності є такий розвиток деформацій у суцільних масивах, коли втрачає силу припущення про мализну розрахункових переміщень порівняно з розмірами розрахункової області. В цьому випадку враховують зміни при деформуванні місцезнаходження (координат) точок розрахункової області. Приклад рішення такої задачі (математичне моделювання НДС основ фундаментів при їх зведенні без виймання ґрунту за різними технологіями та наступній роботі) наведено у п. 10.5.

Зміст поняття нелінійної деформативності ґрунтів і будівельних конструкцій також тісно пов’язаний із можливістю настання їх граничних напружених станів (див. розділ 8). Тому й теорії нелінійного деформування, що використовують для розв’язання задач механіки ґрунтів, містять комплекс перевірок за граничними станами.

Сучасні методи розрахунків дозволяють успішно вирішувати інженерні задачі з урахуванням різних проявів нелінійності. Для цього складені стандартні багатоцільові процедури послідовних наближень або кроків прикладення сил, у яких в якості обчислювальної основи використовують числові методи (див. п. 10.4). Зазначимо, що, на відміну від теорії пружності, нелінійні задачі не мають єдиного рішення. За теорією пластичності поведінка різних матеріалів, у тому числі ґрунту, описують різними рівняннями. Кожне рішення нелінійної задачі являє собою версію відомої багатоцільової процедури у поєднанні з фізичними рівняннями, що описують поведінку конкретних матеріалів і конструкцій з відхиленнями від співвідношень теорії пружності.

10.2. ТЕОРІЇ, ЯКІ ОПИСУЮТЬ НЕЛІНІЙНІ ДЕФОРМАЦІЇ ҐРУНТІВ

У загальному вигляді коректні теорії, що описують нелінійні деформації ґрунтів, базуються на таких уявленнях (Д. М. Шапіро, 1996):

-елементарний об’єм (елемент) ґрунту при зростанні навантаження проходить стадії дограничного й граничного (пластичного) напружених станів, що визначаються фізичними рівняннями теорії пружності та пластичності;

-через нерівномірний розподіл напруг у ґрунтовому масиві мають місце обидва види напруженого стану, які локалізуються в зонах (ділянках), границі яких можливо встановити розрахунком;

-граничні стани (втрата стійкості, прогресуючі переміщення) є наслідком розвитку пластичних областей і накопичення характерних для них деформацій.

Звичайно ґрунт приймають за суцільне ізотропне середовище. Для таких тіл напруже-

ний стан у точці на площині однозначно визначається парою головних напруг σ1 і σ2 (рис. 10.2), а при просторовому напруженому стані – трьома головними напругами σ1, σ2, σ3. Вважають, що для ґрунту характерні два види нелінійності: 1) безперешкодне деформування при розтягненні; 2) пластична формозміна при складному напруженому стані (стиснення із

`

230

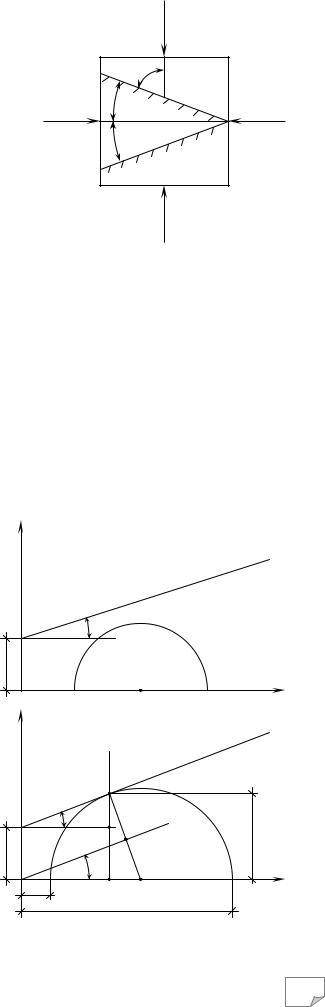
зрушенням).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зв’язок між напругами та деформаціями визначає

 

 

 

 

σ1

 

прийнята модель ґрунту (згадайте п. 6.4), зокрема гра-

 

 

 

 

 

 

фік залежності між напругами та деформаціями досить

 

 

 

 

45°+φ/2

 

популярної у нелінійних задачах механіки ґрунтів моде-

 

 

 

 

 

лі ідеального пружно-пластичного

тіла –

 

лінія

 

3

на

σ2

 

45°-φ/2

σ2

рис. 6.11. Із нього видно, що загальні деформації вклю-

 

 

 

 

 

45°-φ/2

 

чають лінійну (пружну) і пластичну частини, причому

 

 

 

пластична складова деформацій виникає після досяг-

 

 

 

 

 

 

нення напруженим станом межі пропорційності (теку-

 

 

 

 

 

 

чості, міцності).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

За межу пропорційності у точці (елементарному

 

 

 

 

σ1

 

об’ємі) масиву для умови плоскої деформації викорис-

 

 

 

 

 

 

 

 

 

 

 

товують рівняння Мора-Кулона у вигляді

 

 

(σ

 

+σ

 

Рис.

10.2.

Напружений

стан у

 

 

 

 

 

 

 

 

σ

1

−σ

2

 

1

2

)sinϕ

 

(елементарному

об’ємі)

 

 

 

 

 

 

 

 

 

 

+

 

 

 

 

точці

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

−c cosϕ = 0 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ґрунтового масиву

(10.1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

На рис. 10.3 графічно проілюстрована умова міцності Мора-Кулона. Пряма АВ, що

уособлює закон Кулона (див. п.4.6), суміщена з кругами Мора, які показують три якісно різні

напружені стани в точці. Розташування круга Мора з центром у точці О1 нижче від прямої

АВ означає, що ліва частина рівняння (10.1) менша від правої; на всіх площадках, котрі про-

ходять через точку, що розглядається, виконується умова τn <σ ntgϕ + c ; межа пропорційно-

сті не досягнута; міцність ґрунту забезпечена.

 

 

 

 

 

 

 

 

 

 

 

 

 

Дотик прямої АВ до кола Мора з центром у точці О2 показує, що на двох помічених

штрихуванням площадках елементарного об’єму на рис. 10.2 має місце гранична рівновага,

що характеризується залежністю τn =σntgϕ + c ,

і ці площадки нахилені до осей головних

напруг під кутами 45°±φ/2. Рівняння (10.1) може бути отримано з геометричних побудов для

цього

кола:

О2С=О2D+DC;

О2С=(σ1-σ2)/2;

 

 

 

 

τ

 

 

 

 

 

О2D=sinφ(σ1-σ2)/2;

DC=c·cosφ.

Відповідно

 

до

 

 

 

 

 

 

 

 

В

 

 

 

 

 

 

 

 

 

 

 

цих

же

побудов

на

площадці

сковзання

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

→

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(рис.10.3)

дотична

напруга

τn = FC дорівнює

 

 

 

 

 

 

 

 

 

 

 

сумі

відрізків

→

 

та

 

→

 

 

 

 

 

 

 

 

 

 

 

 

φ

 

 

 

FL = c

 

LC =σ ntgϕ

 

 

 

 

А

 

 

 

 

 

 

→

→

→

або τn

=σntgϕ + c

– закон Ку-

 

 

 

 

 

 

 

 

 

 

 

( FC = FL+ CL )

с

 

 

 

 

 

 

 

σ

лона.

Коло Мора не може перетинатися пря-

 

 

 

 

 

 

 

 

 

О1

мою,

 

 

 

 

τ

 

 

 

 

що виражає закон Кулона, бо ґрунт не

 

 

 

 

 

 

 

 

В

сприймає такий напружений стан. Якщо ж за

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

розрахунком таке ж положення все ж отрима-

 

 

 

 

 

 

 

 

 

 

 

не, то це свідчить про недосконалість методу

 

 

 

 

 

 

 

C

 

 

 

визначення компонентів напруг у ґрунтовому

 

 

 

 

 

φ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

середовищі. Рівняння (10.1) пояснює руйнуван-

 

 

 

А

 

 

L

 

 

 

ня ґрунту не як взаємне зміщення частин сипу-

 

 

 

 

 

 

D

 

п

 

 

 

 

 

 

 

 

 

чого тіла (за Кулоном), а як результат формо-

с

 

 

 

 

φ

 

 

τ

змінного впливу прикладених сил.

 

 

 

 

 

 

 

 

 

 

σ1

 

 

 

σ

 

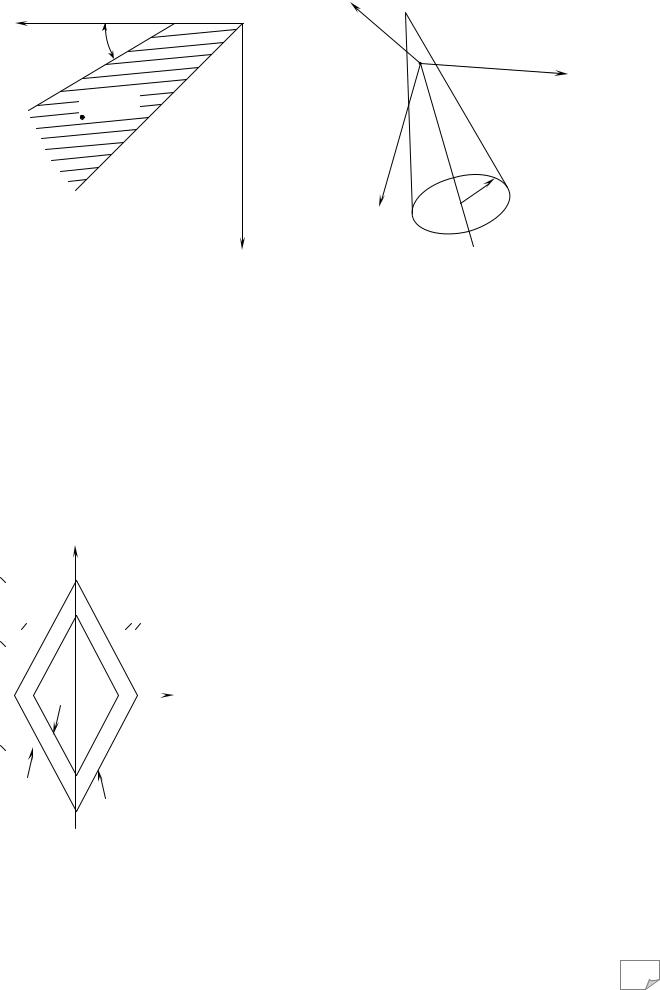
На рис. 10.4, а зображена площина голо-

 

 

 

 

 

F σ2

О2

 

вних напруг σ1,2. Кожна точка М(σ1, σ2) на пло-

 

 

 

 

 

 

 

 

щині зображає поєднання σ1

та σ2, отже, один із

 

 

 

 

 

 

 

 

 

 

 

напружених станів в елементарному об’ємі ґру-

 

 

Рис.

10.3.

Графічна

ілюстрація

умови

нту. Враховуючи, що у даному випадку можливі

 

 

міцності Мора-Кулона

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

231

а)

 

 

б)

 

 

-σ2

A

O

-σ2

 

 

 

 

 

 

 

 

Θ

 

 

O

-σ1

 

 

 

 

 

 

 

 

 

B

M(σ1,σ2)

 

 

 

 

 

σ1=σ2

 

 

 

 

 

C

 

-σ3

r

 

 

 

 

 

 

 

 

 

 

 

 

-σ1

 

C

 

 

 

 

 

 

 

Рис. 10.4. Області фізично можливих напружених станів:

 

 

 

а – на площині; б – у просторі

 

 

лише стискаючі напруги (σ1,2≤0), розглядають четвертину площини, обмежену від’ємними напрямами осей σ1 та σ2. Відповідно до прийнятого σ1≥σ2 частина площини нижче від гідростатичної осі ОС (де σ1=σ2) – недійсна.

Якщо позначити F=(σ1-σ2)/2+(σ1+σ2)(sinφ)/2-c·cosφ, то лінія АВ (рис.10.4, а) зображає

вираз (10.1) F=0; ( OA= − 2 c cosϕ ,

θ = arctg 1

− sinϕ ); точки, розміщені над нею, зобража-

→

 

 

1− sinϕ

1

+ sinϕ

ють напружений стан із порушенням умови F≤0 і закону Кулона. Таким чином, область ф і-

зично можливих сполучень σ1 та σ2

на рис. 10.4, а обмежена фігурою ВАОС. Напружений

стан на межі ВАО, що характеризується рівняннями F=0, σ1=0, вважають граничним; його виникнення у точці ґрунтового масиву вказує на зародження пластичної підобласті й переходу від пружної до пружно-пластичної стадії деформування.

У тілі Гука напрямок векторів головних напруг (σ1,2) і головних відносних деформацій (ε1,2) збігаються або співвісні (коаксіальні). На стадії пласти-

 

 

 

 

 

ε1

 

 

 

чної течії вектори напруг та д еформацій також приймають

 

 

 

 

 

 

 

 

 

співвісними. Однак у цьому випадку цю властивість уводять

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

не як наслідок відомих рівнянь, а у якості самостійного при-

1/2

 

1

ε2/2

пущення, підтвердженого дослідними даними. Отже, також

ε

 

співвісні вектори пружних і пластичних складових головних

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

деформацій ε1,2. Пластичне деформування елементарного

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

об’єму ґрунту відбувається відповідно до схеми, що зображе-

 

 

 

 

 

 

 

ε2

на на рис. 10.5 за рівнянням

 

 

 

 

 

2

 

 

 

 

n

(10.2)

1

 

 

 

 

 

ε1,2 = λ( Λ ±1),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

де ε1n,2 – пластична складова головних деформацій ε1,2; λ –

 

 

 

 

 

 

 

 

 

мала скалярна величина, яка чисельно дорівнює куту зру-

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

шення, λ = (ε1n −ε2n ) / 2 ; Λ – швидкість (параметр)

дилатан-

3сії (постійна, що відображає зміну об’єму при формозміні (зрушенні) ґрунту). З рівняння (10.2) виходить, що

Рис. 10.5. Формозміна та ди-

Λ =

(ε n +ε n ) /(ε n

−ε n ) .

 

1

2

1

 

2

латансія елементарного об’є-

Коефіцієнт Λ ≠ 0 відрізняє форму деформації відпо-

му ґрунту при пластичному

відно до (10.2) від чистого зрушення (Λ = 0 ), де

ε n

 

= ±λ , а

деформуванні: 1 – початкові

 

 

 

1,2

 

розміри; 2 – чисте зрушення

на площадках, нахилених до осей головних напруг під кутом

(Λ =0); 3 – формозміна з ди-

45 , має місце επ / 4 = 0, γπn / 4 = 0,5 (ε1n −ε2n ) = λ .

 

 

 

латансією (Λ >0)

 

 

 

 

 

 

`

 

 

 

 

 

232
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности