
- •Передмова
- •Вступ
- •Частина перша
- •1. ОСНОВНІ ВІДОМОСТІ ПРО ЗЕМЛЮ. МІНЕРАЛИ І ГІРСЬКІ ПОРОДИ
- •1.1. ЗЕМЛЯ У СВІТОВОМУ ПРОСТОРІ, ЇЇ ПОХОДЖЕННЯ І БУДОВА
- •1.2. МІНЕРАЛИ, ЇХ КЛАСИФІКАЦІЯ І ФІЗИЧНІ ВЛАСТИВОСТІ
- •1.3. ГІРСЬКІ ПОРОДИ, ЇХ ПОХОДЖЕННЯ ТА ВІДМІТНІ ОЗНАКИ
- •1.4. ВІК ГІРСЬКИХ ПОРІД І ШКАЛА ГЕОЛОГІЧНОГО ЧАСУ
- •2. ГЕОЛОГІЧНІ ТА ІНЖЕНЕРНО-ГЕОЛОГІЧНІ ПРОЦЕСИ
- •2.2. РУХИ ЗЕМНОЇ КОРИ ТА ДИСЛОКАЦІЇ
- •2.3. МАГМАТИЗМ І ВУЛКАНИ
- •2.4. ЗЕМЛЕТРУСИ
- •2.5. ВИВІТРЮВАННЯ ТА ЕЛЮВІАЛЬНІ ВІДКЛАДИ
- •2.7. ГЕОЛОГІЧНА РОБОТА ЛЬОДОВИКІВ І ЛЬОДОВИКОВІ ВІДКЛАДИ
- •2.8. ГЕОЛОГІЧНА РОБОТА ВІТРУ ТА ЕОЛОВІ ВІДКЛАДИ
- •2.9. ГЕОЛОГІЧНА РОБОТА МОРЯ І МОРСЬКІ ВІДКЛАДИ
- •2.10. ВІДКЛАДИ ОЗЕР І БОЛІТ
- •2.11. ЧЕТВЕРТИННІ ТА КОРІННІ ВІДКЛАДИ
- •2.12. ПЛИВУНИ ТА ОСОБЛИВОСТІ ЗВЕДЕННЯ НА НИХ БУДІВЕЛЬ І СПОРУД
- •2.13. СУФОЗІЯ
- •2.14. КАРСТ
- •2.15. ЗСУВИ
- •3. ОСНОВИ ГІДРОГЕОЛОГІЇ
- •3.1. КРУГООБІГ ВОДИ В ПРИРОДІ
- •3.2. ПОХОДЖЕННЯ І ФОРМУВАННЯ ПІДЗЕМНИХ ВОД
- •3.3. ВИДИ ВОДИ В ПОРАХ ГІРСЬКИХ ПОРІД
- •3.4. ФІЗИЧНІ ВЛАСТИВОСТІ, ХІМІЧНИЙ І БАКТЕРІАЛЬНИЙ СКЛАД ПІДЗЕМНИХ ВОД ТА ЇХ АГРЕСИВНІСТЬ
- •3.5. КЛАСИФІКАЦІЯ ПІДЗЕМНИХ ВОД
- •3.6. ХАРАКТЕРИСТИКА ПІДЗЕМНИХ ВОД
- •3.7. РУХ ВОДИ В ГІРСЬКИХ ПОРОДАХ
- •3.8. РОЗРАХУНОК ВИТРАТ ПОТОКУ ҐРУНТОВИХ ВОД ТА ПРИПЛИВУ ВОДИ ДО ВОДОЗАБІРНИХ СПОРУД
- •3.9. ВЗАЄМОДІЯ СВЕРДЛОВИН І ОРГАНІЗАЦІЯ ВОДОЗНИЖЕННЯ
- •3.10. ГІДРОГЕОЛОГІЧНІ ДОСЛІДЖЕННЯ
- •3.11. ЗАПАСИ ПІДЗЕМНИХ ВОД ТА ЇХ ОХОРОНА
- •4. ОСНОВИ ҐРУНТОЗНАВСТВА
- •4.1. СКЛАДОВІ КОМПОНЕНТИ ТА СТРУКТУРНІ ЗВ’ЯЗКИ ҐРУНТІВ
- •4.2. ФІЗИЧНІ ХАРАКТЕРИСТИКИ ҐРУНТІВ
- •4.3. КЛАСИФІКАЦІЯ ҐРУНТІВ
- •4.4. ЗАГАЛЬНА ХАРАКТЕРИСТИКА МЕХАНІЧНИХ ВЛАСТИВОСТЕЙ ҐРУНТІВ
- •4.5. СТИСЛИВІСТЬ ҐРУНТІВ, ВИЗНАЧЕННЯ ХАРАКТЕРИСТИК СТИСЛИВОСТІ. ЗАКОН УЩІЛЬНЕННЯ
- •4.6. МІЦНІСТЬ ҐРУНТІВ, ВИЗНАЧЕННЯ ХАРАКТЕРИСТИК МІЦНОСТІ. ЗАКОН КУЛОНА
- •4.7. ВИЗНАЧЕННЯ РОЗРАХУНКОВИХ ХАРАКТЕРИСТИК ФІЗИКО-МЕХАНІЧНИХ ВЛАСТИВОСТЕЙ ҐРУНТІВ
- •4.8. ЗВ’ЯЗОК МІЖ ФІЗИЧНИМИ ТА МЕХАНІЧНИМИ ХАРАКТЕРИСТИКАМИ ҐРУНТІВ
- •4.9. ДИЛАТАНСІЯ ҐРУНТУ
- •4.10. АНІЗОТРОПІЯ ҐРУНТУ
- •4.11. РЕОЛОГІЧНІ ВЛАСТИВОСТІ ҐРУНТІВ
- •4.12. ДИНАМІЧНІ ВЛАСТИВОСТІ ҐРУНТІВ
- •5. ІНЖЕНЕРНО-ГЕОЛОГІЧНІ ДОСЛІДЖЕННЯ
- •5.1. СКЛАД І ОБ’ЄМ ІНЖЕНЕРНО-ГЕОЛОГІЧНИХ ДОСЛІДЖЕНЬ
- •5.2. ІНЖЕНЕРНО-ГЕОЛОГІЧНА РЕКОГНОСЦИРОВКА
- •5.3. ІНЖЕНЕРНО-ГЕОЛОГІЧНА ЗЙОМКА
- •5.4. ІНЖЕНЕРНО-ГЕОЛОГІЧНА РОЗВІДКА
- •5.5. ГІРСЬКІ ТА БУРОВІ ВИРОБКИ
- •5.6. ПОЛЬОВІ ДОСЛІДНІ РОБОТИ
- •5.7. ЛАБОРАТОРНІ РОБОТИ
- •5.8. ІНЖЕНЕРНО-ГЕОЛОГІЧНА ЕКСПЕРТИЗА
- •5.9. КАМЕРАЛЬНІ РОБОТИ
- •5.10. ОСОБЛИВОСТІ ІНЖЕНЕРНО-ГЕОЛОГІЧНИХ ДОСЛІДЖЕНЬ У РАЙОНАХ РОЗВИТКУ НЕБЕЗПЕЧНИХ ІНЖЕНЕРНО-ГЕОЛОГІЧНИХ ПРОЦЕСІВ
- •5.11. ВИКОРИСТАННЯ ГЕОФІЗИЧНИХ МЕТОДІВ
- •Частина друга
- •6. ЕКСПЕРИМЕНТАЛЬНО-ТЕОРЕТИЧНІ ПЕРЕДУМОВИ МЕХАНІКИ ҐРУНТІВ
- •6.1. ЗАГАЛЬНІ УЯВЛЕННЯ ПРО ҐРУНТ І РОЗВИТОК МЕХАНІКИ ҐРУНТІВ
- •6.2. ФАЗИ НАПРУЖЕНОГО СТАНУ ҐРУНТУ
- •6.3. ОСНОВНІ ПОЛОЖЕННЯ ПРО РОЗПОДІЛ НАПРУГ І ДЕФОРМАЦІЙ У ТОЧЦІ МАСИВУ ҐРУНТУ
- •6.4. МОДЕЛІ, ЩО ОПИСУЮТЬ СТАН ҐРУНТУ
- •7.2. РОЗПОДІЛ НАПРУГ ВІД ВЛАСНОЇ ВАГИ ҐРУНТУ
- •7.3. РОЗПОДІЛ НАПРУГ ПО ПІДОШВІ ФУНДАМЕНТІВ
- •7.4. МЕТОДИ ВИМІРЮВАННЯ НАПРУГ У ҐРУНТАХ
- •7.5. ВИДИ ДЕФОРМАЦІЙ ҐРУНТІВ І ПРИЧИНИ, ЯКІ ЇХ ЗУМОВЛЮЮТЬ
- •7.6. ВИЗНАЧЕННЯ ОСІДАННЯ ШАРУ ҐРУНТУ ПРИ СУЦІЛЬНОМУ НАВАНТАЖЕННІ (ОСНОВНА ЗАДАЧА)
- •7.7. ПРАКТИЧНІ МЕТОДИ ВИЗНАЧЕННЯ ОСІДАНЬ ОСНОВИ
- •7.8. УРАХУВАННЯ ВПЛИВУ ЗАВАНТАЖЕННЯ СУСІДНІХ ФУНДАМЕНТІВ
- •8. ТЕОРІЯ ГРАНИЧНОГО НАПРУЖЕНОГО СТАНУ ҐРУНТІВ І ЇЇ ЗАСТОСУВАННЯ
- •8.1. РІВНЯННЯ ГРАНИЧНОЇ РІВНОВАГИ ДЛЯ СИПУЧИХ ТА ЗВ’ЯЗНИХ ҐРУНТІВ
- •8.2. ВИЗНАЧЕННЯ ПЕРШОГО КРИТИЧНОГО ТИСКУ НА ҐРУНТ
- •8.3. ВИЗНАЧЕННЯ ДРУГОГО КРИТИЧНОГО ТИСКУ НА ҐРУНТ
- •8.4. ВПЛИВ РІЗНОМАНІТНИХ ФАКТОРІВ НА ХАРАКТЕР РУЙНУВАННЯ ОСНОВ І ГРАНИЧНИЙ ТИСК
- •8.5. СТІЙКІСТЬ УКОСІВ ҐРУНТУ
- •8.6. ВИЗНАЧЕННЯ ТИСКУ ҐРУНТІВ НА ОГОРОЖІ
- •9. ГРАНИЧНИЙ НАПРУЖЕНИЙ СТАН АНІЗОТРОПНИХ ОСНОВ
- •9.1. УМОВИ ГРАНИЧНОГО НАПРУЖЕНОГО СТАНУ АНІЗОТРОПНОГО ЗА ОПОРОМ ЗРУШЕННЮ ҐРУНТУ І РОЗРАХУНКОВА МОДЕЛЬ
- •9.2. ВИРІШЕННЯ ЗАДАЧ ДЛЯ АНІЗОТРОПНОЇ ЗА ОПОРОМ ЗРУШЕННЮ ОСНОВИ
- •9.3. ВИРІШЕННЯ ПРАКТИЧНИХ ЗАДАЧ ДЛЯ АНІЗОТРОПНОГО ЗА ОПОРОМ ЗРУШЕННЮ ҐРУНТУ.
- •10. ЗАСТОСУВАННЯ ТЕОРІЇ НЕЛІНІЙНОГО ДЕФОРМУВАННЯ ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ МЕХАНІКИ ҐРУНТІВ
- •10.1. СУЧАСНІ УЯВЛЕННЯ ПРО НЕЛІНІЙНУ ДЕФОРМАТИВНІСТЬ ҐРУНТІВ
- •10.2. ТЕОРІЇ, ЯКІ ОПИСУЮТЬ НЕЛІНІЙНІ ДЕФОРМАЦІЇ ҐРУНТІВ
- •10.3. ПРАКТИЧНІ МЕТОДИ УРАХУВАННЯ НЕЛІНІЙНОЇ ДЕФОРМАТИВНОСТІ ҐРУНТІВ У РОЗРАХУНКАХ ОСНОВ
- •10.4. ТЕОРЕТИЧНІ ОСНОВИ ЧИСЛОВИХ МЕТОДІВ
- •10.5. ЧИСЛОВІ МЕТОДИ У ЗАДАЧАХ МЕХАНІКИ ҐРУНТІВ
- •10.6. ВИКОРИСТАННЯ РІШЕНЬ ТЕОРІЇ ФІЛЬТРАЦІЙНОЇ КОНСОЛІДАЦІЇ ҐРУНТІВ ДЛЯ ПРОГНОЗУ ОСІДАННЯ ОСНОВ У ЧАСІ
- •10.7. ПРИКЛАДНА ТЕОРІЯ ПОВЗУЧОСТІ ҐРУНТІВ У РОЗРАХУНКАХ ДЕФОРМАЦІЙ ОСНОВ У ЧАСІ
- •10.8. ПРОГНОЗ РОЗВИТКУ ДЕФОРМАЦІЙ ОСНОВИ З ЧАСОМ ЗА ДАНИМИ ІНСТРУМЕНТАЛЬНИХ СПОСТЕРЕЖЕНЬ ЗА НИМИ
- •11. ОСНОВИ ТЕОРІЇ УЩІЛЬНЕННЯ ҐРУНТІВ
- •11.1. ЗАГАЛЬНІ ПОНЯТТЯ ПРО УЩІЛЬНЕННЯ ҐРУНТІВ ТА ЇХ ОПТИМАЛЬНІ ХАРАКТЕРИСТИКИ
- •11.2. СТАНДАРТНИЙ МЕТОД УЩІЛЬНЕННЯ ҐРУНТІВ
- •11.3. ДИНАМІЧНИЙ МЕТОД УЩІЛЬНЕННЯ ҐРУНТІВ
- •11.4. ПОЛЬОВІ ДОСЛІДЖЕННЯ УЩІЛЬНЕННЯ ҐРУНТІВ
- •11.5. ВИЗНАЧЕННЯ ОПТИМАЛЬНИХ ХАРАКТЕРИСТИК УЩІЛЬНЕННЯ З УРАХУВАННЯМ ПАРАМЕТРІВ МЕХАНІЗМІВ ДЛЯ УЩІЛЬНЕННЯ ҐРУНТУ
- •11.6. ВИЗНАЧЕННЯ ХАРАКТЕРИСТИК УЩІЛЬНЕННЯ ЗА УМОВИ ЗАБЕЗПЕЧЕННЯ ТРИВАЛОЇ МІЦНОСТІ ҐРУНТІВ
- •11.7. ОСОБЛИВОСТІ УТВОРЕННЯ В ҐРУНТІ УЩІЛЬНЕНИХ ЗОН
- •Частина третя
- •12. ПРИНЦИПИ ПРОЕКТУВАННЯ ОСНОВ І ФУНДАМЕНТІВ
- •12.2. ПРИНЦИПИ ПРОЕКТУВАННЯ ОСНОВ ЗА ГРАНИЧНИМИ СТАНАМИ
- •12.3. ВЗАЄМОДІЯ ФУНДАМЕНТІВ І ШТУЧНИХ ОСНОВ ІЗ ҐРУНТОМ, ЩО ЇХ ОТОЧУЄ
- •12.4. ВИХІДНІ ДАНІ ДЛЯ ПРОЕКТУВАННЯ ОСНОВ І ФУНДАМЕНТІВ
- •12.5. ЗАВДАННЯ ВАРІАНТНОСТІ ПРИ ПРОЕКТУВАННІ ОСНОВ І ФУНДАМЕНТІВ
- •12.6. ВИБІР ГЛИБИНИ ЗАКЛАДАННЯ ФУНДАМЕНТІВ
- •13. ФУНДАМЕНТИ ТА ШТУЧНІ ОСНОВИ, ЯКІ ВИГОТОВЛЯЮТЬ ІЗ ВИЙМАННЯМ ҐРУНТУ
- •13.1. КОНСТРУКЦІЇ ФУНДАМЕНТІВ НЕГЛИБОКОГО ЗАКЛАДАННЯ
- •13.2. РОЗРАХУНОК ФУНДАМЕНТІВ НЕГЛИБОКОГО ЗАКЛАДАННЯ ВІД ДІЇ ВЕРТИКАЛЬНОГО І ГОРИЗОНТАЛЬНОГО НАВАНТАЖЕННЯ
- •13.4. ФУНДАМЕНТИ, ЯКІ ВИГОТОВЛЯЮТЬСЯ З ВИКОРИСТАННЯМ БУРІННЯ
- •13.5. ОПУСКНІ КОЛОДЯЗІ І КЕСОНИ
- •13.6. ФУНДАМЕНТИ ТИПУ “СТІНА В ҐРУНТІ”
- •13.7. ПІЩАНІ І ҐРУНТОВІ ПОДУШКИ
- •14. ФУНДАМЕНТИ І ШТУЧНІ ОСНОВИ, ЯКІ ВИГОТОВЛЯЮТЬ БЕЗ ВИЙМАННЯ ҐРУНТУ
- •14.3. ВИЗНАЧЕННЯ НЕСУЧОЇ ЗДАТНОСТІ ПАЛЬ І ФУНДАМЕНТІВ
- •14.4. ОСОБЛИВОСТІ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ НАПРУЖЕНО-ДЕФОРМОВАНОГО СТАНУ ОСНОВ ПРИ ВЛАШТУВАННІ І РОБОТІ ФУНДАМЕНТІВ, ЯКІ ВИГОТОВЛЯЮТЬСЯ БЕЗ ВИЙМАННЯ ҐРУНТУ
- •14.5. ПРОЕКТУВАННЯ ФУНДАМЕНТІВ, ЯКІ ВИГОТОВЛЯЮТЬСЯ БЕЗ ВИЙМАННЯ ҐРУНТУ
- •14.6. РІЗНОВИДИ ШТУЧНИХ ОСНОВ, ЯКІ ВИГОТОВЛЯЮТЬ МЕТОДОМ УЩІЛЬНЕННЯ БЕЗ ВИЙМАННЯ ҐРУНТУ
- •15. ШТУЧНІ ОСНОВИ, ЯКІ УТВОРЮЮТЬ ЗА ДОПОМОГОЮ ФІЗИКО-ХІМІЧНИХ ПРОЦЕСІВ
- •15.1. ЗАГАЛЬНІ ПОЛОЖЕННЯ
- •15.2. ПОЛІПШЕННЯ ҐРУНТУ ОСНОВИ ЧЕРЕЗ НАГНІТАННЯ В’ЯЖУЧОЇ РЕЧОВИНИ
- •15.3. ТЕРМОЗАКРІПЛЕННЯ ҐРУНТІВ
- •15.4. ЕЛЕКТРОХІМІЧНЕ ЗАКРІПЛЕННЯ ҐРУНТІВ
- •16. ФУНДАМЕНТИ БУДІВЕЛЬ І СПОРУД У СКЛАДНИХ ІНЖЕНЕРНО-ГЕОЛОГІЧНИХ УМОВАХ
- •16.1 ЗАГАЛЬНІ ПОЛОЖЕННЯ
- •16.2. ФУНДАМЕНТИ НА ЛЕСОВИХ ПРОСАДОЧНИХ ҐРУНТАХ
- •16.3. ФУНДАМЕНТИ НА ҐРУНТАХ, ЯКІ ЗДАТНІ ДО НАБУХАННЯ
- •16.4. ФУНДАМЕНТИ НА СЛАБКИХ ҐРУНТАХ
- •16.5. ФУНДАМЕНТИ НА НАСИПНИХ І НАМИВНИХ ҐРУНТАХ
- •16.6. ФУНДАМЕНТИ НА ЗАСОЛЕНИХ ҐРУНТАХ
- •16.7. ФУНДАМЕНТИ В УМОВАХ СЕЗОННОЇ І ВІЧНОЇ МЕРЗЛОТИ
- •16.8. ОСНОВИ І ФУНДАМЕНТИ В УМОВАХ ПІДТОПЛЕНИХ ТЕРИТОРІЙ
- •16.9. УЛАШТУВАННЯ ОСНОВ І ФУНДАМЕНТІВ НА ДІЛЯНКАХ, ПІД ЯКИМИ Є ПІДЗЕМНІ ВИРОБКИ
- •16.10. ФУНДАМЕНТИ В КАРСТОВИХ РАЙОНАХ
- •16.11. ПРОЕКТУВАННЯ ФУНДАМЕНТІВ В УМОВАХ ТЕХНОГЕННОГО ВПЛИВУ
- •16.12. ФУНДАМЕНТИ НА ЗСУВНИХ ТЕРИТОРІЯХ
- •17. ФУНДАМЕНТИ ПРИ ДИНАМІЧНИХ ВПЛИВАХ
- •17.1. ОСОБЛИВОСТІ ДИНАМІЧНИХ ВПЛИВІВ НА СПОРУДИ І ҐРУНТОВІ ОСНОВИ
- •17.2. ТИПИ ФУНДАМЕНТІВ ПІД МАШИНИ Й ОБЛАДНАННЯ З ДИНАМІЧНИМИ НАВАНТАЖЕННЯМИ
- •17.3. РОЗРАХУНКИ ОСНОВ І ФУНДАМЕНТІВ ПРИ ДИНАМІЧНИХ НАВАНТАЖЕННЯХ
- •17.6. ОСОБЛИВОСТІ ПРОЕКТУВАННЯ СЕЙСМОСТІЙКИХ ФУНДАМЕНТІВ І СПОРУД
- •18.1 ВЗАЄМОДІЯ ФУНДАМЕНТІВ З ОСНОВОЮ
- •18.2. МЕТОДИ ВРАХУВАННЯ СПІЛЬНОЇ РОБОТИ СИСТЕМИ “ОСНОВА–ФУНДАМЕНТ–БУДІВЛЯ”
- •18.3. РОЗРАХУНКОВІ МОДЕЛІ ҐРУНТОВОЇ ОСНОВИ
- •18.4. КОЕФІЦІЄНТИ ЖОРСТКОСТІ ОСНОВИ ПРИ НЕРІВНОМІРНОМУ СТИСКУ І ЗРУШЕННІ. КОЕФІЦІЄНТИ ЖОРСТКОСТІ ПАЛЬОВИХ ОСНОВ. КОЕФІЦІЄНТИ ЖОРСТКОСТІ ПРОСАДОЧНОЇ ОСНОВИ. РЕОЛОГІЧНІ КОЕФІЦІЄНТИ ЖОРСТКОСТІ
- •18.5. РОЗРАХУНОК БАЛОК І ПЛИТ НА ДЕФОРМОВАНІЙ ОСНОВІ
- •18.6. РОЗРАХУНОК РАМ НА ДЕФОРМОВАНІЙ ОСНОВІ
- •18.7. КОНТИНУАЛЬНІ КІНЦЕВО-ЕЛЕМЕНТНІ РОЗРАХУНКОВІ СХЕМИ ФУНДАМЕНТІВ І СПОРУД НА ДЕФОРМОВАНІЙ ОСНОВІ.
- •19. ОСНОВИ НАДІЙНОСТІ ТА ЕКОНОМІЧНОСТІ ФУНДАМЕНТОБУДУВАННЯ
- •19.1. ЧИННИКИ ТЕОРІЇ НАДІЙНОСТІ СИСТЕМИ “ОСНОВА – ФУНДАМЕНТ – СПОРУДА”
- •19.2. РОЗРАХУНОК ОСНОВ І ФУНДАМЕНТІВ НА НАДІЙНІСТЬ ТА ВИКОРИСТАННЯ ХАРАКТЕРИСТИК НАДІЙНОСТІ В ПРАКТИЦІ ЇХ ПРОЕКТУВАННЯ
- •19.3. ПРИЧИНИ ЗНИЖЕННЯ І ЗАХОДИ ЗАБЕЗПЕЧЕННЯ НАДІЙНОСТІ ОСНОВ І ФУНДАМЕНТІВ
- •19.4. МЕТОДИ ОЦІНЮВАННЯ ЕФЕКТИВНОСТІ РІЗНОВИДІВ ОСНОВ І ФУНДАМЕНТІВ
- •19.5. ЕКОНОМІЯ ЕНЕРГОРЕСУРСІВ ПРИ ПРОЕКТУВАННІ І ВЛАШТУВАННІ ОСНОВ ТА ФУНДАМЕНТІВ
- •19.6. ОХОРОНА НАВКОЛИШНЬОГО СЕРЕДОВИЩА ПРИ ВЛАШТУВАННІ ФУНДАМЕНТІВ
- •Список рекомендованої літератури

Таблиця 7.1. Залежність коефіцієнта k від η |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Η |
1,0 |
1,2 |
1,4 |
|
1,6 |
1,8 |
2,0 |
≥6,0 (стрічка) |
K |
2,0 |
2,2 |
2,4 |
|
2,6 |
2,8 |
2,9 |
5,5 |
Розрахунок осідання методом лінійно деформівного шару
Розрахункова схема осідання лінійно деформівного шару подана на рис. 7.18. Цей метод розрахунку осідань застосовують у таких випадках:
а) якщо у межах товщі основи, яка стискується, Hc залягає шар ґрунту з модулем деформації E1>100 МПа завтовшки h1 і виконується умова
h1 ≥ Hc (1− |
|
), |
(7.49) |
E2 E1 |
де E2 – модуль деформації шару ґрунту, що підстилає шар із модулем деформа-
ції E1;б) якщо ширина або діаметр фундаменту b≥10 м і модуль деформації складає E≥10 МПа. Товщина лінійно деформівного шару H у випадку а) приймається до покрівлі ґрунту з модулем деформації E≥100 МПа, у випадку б) визначається за виразом
H = (H0 +ψb)kp , |
(7.50) |
де H0 та ψ – приймають рівними для основ із глинистих ґрунтів відповідно 9 м і 0,15, а для піщаних – 6 м та 0,1; kp – коефіцієнт, який приймають при середньому тиску під підошвою фундаменту p=100 кПа kp=0,8, а при p=500 кПа kp=1,2; для проміжних значень kp визначають за інтерполяцією. Осідання основи фундаменту визначають з виразу
S = |
pbk |
n |
k |
− k |
(7.51) |
km |
c ∑ |
i |
i−1 , |
||
|
i=1 |
|
Ei |
|
де p – середній тиск під підошвою фундаменту (для b<10 м приймають p=p0, де p0 = p −σ zg0 ); kc і km – коефіцієнти, які визначають за допомогою СНиП
2.02.01-83; n – кількість шарів, котрі відрізняються стисливістю в межах розрахункової потужності H шару, що стискується; ki та ki-1 – коефіцієнти, які визначають із таблиці 4 додатку 2 СНиП 2.02.01-83; Ei – модуль деформації і-гo шару.
7.8. УРАХУВАННЯ ВПЛИВУ ЗАВАНТАЖЕННЯ СУСІДНІХ ФУНДАМЕНТІВ
Якщо на близькій відстані від фундаменту, осідання якого розраховують, розташовані сусідні фундаменти, вони можуть впливати на величину осідання. Тому при розрахунку осідання потрібно побудувати спочатку епюру додаткових вертикальних напруг σzp для фундаменту, що розраховується. Потім визначають додаткові напруги, котрі виникають уздовж вертикалі, що проходить крізь центр підошви фундаменту, від впливу сусідніх фундаментів і будують сумарну епюру додаткових вертикальних напруг. На рис. 7.19, а показана схема побудування епюр додаткових напруг та розміщення меж товщі, яка стискується. Видно, що збільшення кількості близько розташованих фундаментів при-
` |
184 |
а |
1 |
|
2 |
3 |
|
|
|
|
|
|
В.С2 |
σzp2 |
|
|
|
|
|
|
|
|
В.С2+1 |
σzp2+1 |
σzp2+1+3 |
|
|
|
|
|
|
|
В.С2+1+3 |
|
|
|
б |
|
|
|
|
|
i=1 |
i=2 |
i=3 |
i=4 |
|
1 |
|
– |
|
|
+ |
|
+ |
|
|
– |
|
||
|
|
|
|
|
|
A |
A |
A |
A |
|
2 |
|
|
|
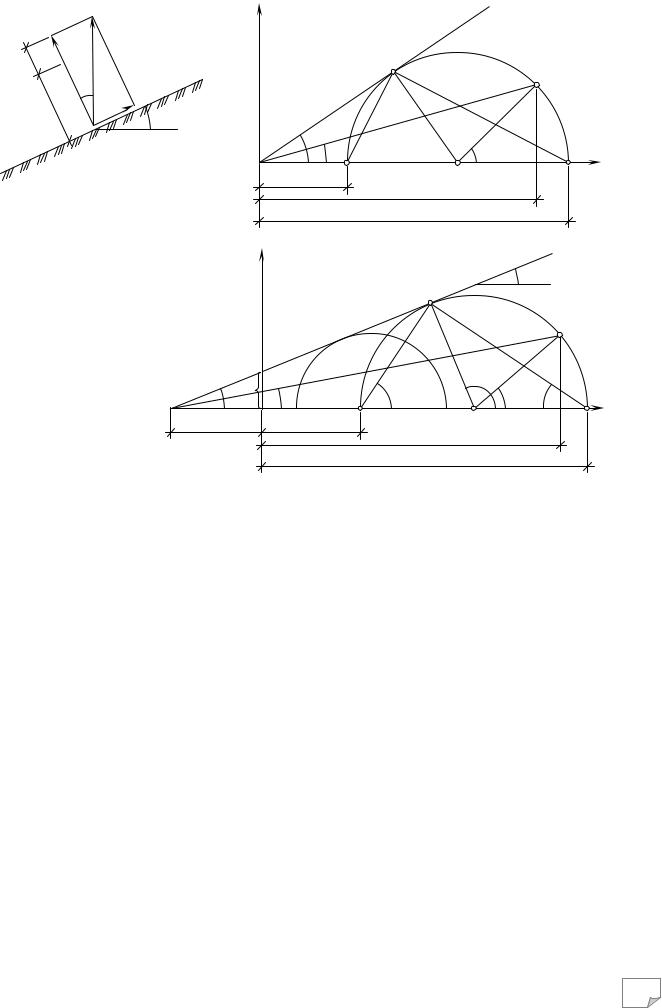
Рис. 7.19. Урахування впливу сусідніх фундаментів: а – схема побудови епюр додаткових |
||||
напруг і розміщення меж стисливої товщі; |
б – схема розташування фіктивних фундаментів |
|||
при визначенні додаткових напруг у точці А від фундаменту; 1, 3 – фундаменти, що впли- |
||||
вають на фундамент, який розраховують; 2 – фундамент, котрий розраховують |
||||
водить до зростання сумарної епюри додаткових напруг. Потужність товщі, котра стискується, також зростає.
Додаткові вертикальні напруги від впливу сусідніх фундаментів σzp,a можуть бути визначені за допомогою методу кутових точок. На рис. 7.19, б показана схема розміщення фіктивних фундаментів при визначенні додаткових напруг у точці А фундаменту 2 від фундаменту 1.
Величину σzp,a визначають алгебраїчним підсумовуванням напруг σzp,ci у кутових точках чотирьох фіктивних фундаментів за допомогою формули
n |
|
σ zp,a = ∑σ zp,ci . |
(7.52) |
1 |
|
Знаки напруг σzp,ci у формулі (7.52) під кутом і-го фундаменту приймають відповідно до схеми на рис. 7.19, б.
Якщо виникає необхідність урахування впливу кількох сусідніх фундаментів, для кожного з них за допомогою ф ормули (7.52) визначають додаткову вертикальну напругу, а потім будують сумарну епюру σzp, яка враховує вплив
185

усіх фундаментів. Після побудування епюри розрахунок осідання можливо виконати методом пошарового підсумовування або іншими методами.
У виробничих будівлях, що мають підлогу, розміщену безпосередньо на ґрунті, при побудові епюри додаткових вертикальних напруг необхідно враховувати навантаження на підлогу
σ zp,nf =σ zp + q , |
(7.53) |
де q – інтенсивність рівномірно розподіленого навантаження на підлогу.
8. ТЕОРІЯ ГРАНИЧНОГО НАПРУЖЕНОГО СТАНУ ҐРУНТІВ І ЇЇ ЗАСТОСУВАННЯ
8.1. РІВНЯННЯ ГРАНИЧНОЇ РІВНОВАГИ ДЛЯ СИПУЧИХ ТА ЗВ’ЯЗНИХ ҐРУНТІВ
Гранична рівновага відповідає такому станові масиву ґрунту, коли найменше збільшення навантаження приводить до втрати стійкості.
Розглянемо дію на поверхню ґрунту місцевого навантаження в довільній точці ґрунту М (рис. 8.1, а) для довільної площадки mn, що проходить через цю точку під кутом αi. У точці М виникають нормальні й дотичні напруги. До нормальних напруг при математичному розгляді питання можна віднести також тиск зв’язності pε (рис. 8.1, в), що чисельно дорівнює pε=c·ctgφ. Тоді на площадку mn будуть діяти нормальна напруга σαi + pε та дотична ταi .
При зміні кута αi складові напруг також будуть змінюватися, і, коли дотичні (зсуваючі) напруги досягнуть деякої частини нормальних, виникне, як показують досліди на зсув, ковзання однієї частини ґрунту вздовж другої.
Таким чином, умовою граничної рівноваги ґрунту буде
ταi ≤ f (σαi + pε ) |
(8.1) |
|||
або |
|
|
|
|
|
τα |
|
≤ f , |
(8.2) |
σα + pε |
||||
|
|
i |
|
|
i
де f – постійна величина, котра в граничному стані є тангенс кута нахилу прямолінійної обвідної кіл граничних напруг.
У свою чергу, відповідно до рис. 8.1, а,
τα |
|
= tgθ , |
(8.3) |
|
σα |
+ pε |
|||
|
|
i |
|
|
i
де tgθ – тангенс кута відхилення θ, тобто кута, на який відхиляється повна напруга для площадки σ від нормалі до цієї площадки.
Через точку М можна провести безліч площадок, подібних mn, тому необхідно відшукати найбільш невигідну, для котрої буде існувати максимальний кут відхилення θ.
Тоді
` |
186 |
а |
|
|
σ |
б |
τ |
|
|
|
|
|
pε |
θ |
|
n |
|
|
|
E |
M |
|
|
ταi |
|
|
|
|
|||
|
σαi |
|
|
|
|
|
|
|
|
|
|
αi |
|
|
θmax=φ |
|
|
ταi |
|
|
|
|
|
|
|
|
|||
m |
|
|
M |
|
O |
|
θ |
2α |
σ |
|
|
|
|
|
|||||
|
|
|
|
|
σ2 |
A |
C |
B |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
σαi |
|
|
|
|
|
|
|
|
|
σ1 |
|
|
|
|
|
в |
τ |
|
|
|
θmax=φ |
|
|
|
|
|
|
|
|
E |
|
Рис. 8.1. Діаграма граничних напруг: |
|
|
|
|
|||||
а – схема напруг у точці масиву; |
|
|
|
|
M |
||||
б – для незв’язного ґрунту; |
|
|
|
|
|
||||
в – для зв’язного ґрунту |
|
|
|
|
|
|
|||
|
φ |
c |
|
|
45°+φ/2 2β |
2α |
ταi |
|
θ |
|
σ |
||||
O |
pε |
O1 |
σ2 |
A |
C |
|
45°-φ/2 B |
|
|
|
|
|
σαi |
|
|
|
|
|
|
|
σ1 |
|
|
|
|
tgθmax ≤ f . |
|
|
|
(8.4) |
|
Розглянемо умови граничної рівноваги для сипучих і зв’язних ґрунтів. Для сипучих ґрунтів відповідно до діаграми зсуву (рис. 8.1, б) максимального значення кут відхилення досягне тоді, коли обвідна ОЕ стане дотичною до кола граничних напруг.
Із трикутника ОЕС видно, що
sinϕ = |
EC ; |
EC = |
σ1 −σ2 |
; |
|
|
OC |
|
|
2 |
|
OC =σ2 + σ1 −σ2 = |
σ1 +σ2 . |
||||
Тоді |
|
2 |
|
2 |
|
|
σ1 −σ2 |
|
|
||
|
sinϕ = |
, |
(8.5) |
||
|
|
σ1 +σ2 |
|
|
|
де σ1 та σ2 – головні напруги; φ – кут внутрішнього тертя ґрунту.
Вираз (8.5) і є умовою граничної рівноваги для сипучих ґрунтів. Після нескладних тригонометричних перетворень цьому виразові можна надати іншого вигляду
σ2 |
=σ1 |
|
1 |
− sinϕ |
, |
(8.6) |
|
1 |
+ sinϕ |
||||||
|
|
|
|
||||
або
187

σ |
2 |
= tg 2 |
|
45 ± |
ϕ |
(8.7) |
|
|
|
2 |
. |
||||
σ1 |
|
|
|
|
|
||
Вираз (8.7) широко застосовується для розрахунків тиску на огороджуючі конструкції.
Для зв’язних ґрунтів відповідно до діаграми граничних напруг (рис. 8.1, в) одержимо умову граничної рівноваги у вигляді
|
|
|
|
|
|
|
σ1 −σ2 |
|
= sinϕ , |
|
|
(8.8) |
|||
звідки |
|
|
σ1 +σ2 + 2 pε |
|
|
|
|||||||||
|
|
|
|
|
|
σ |
|
|
+σ |
|
|
|
|
||
|
σ |
|
−σ |
|
|
|
1 |
2 + p |
|
(8.9) |
|||||
|
1 |
2 |
= 2 sinϕ |
2 |
. |
||||||||||
|
|
|
|
|
|
|
|
|
ε |
|
|
||||
Оскільки pε=c·ctgφ, то вираз (8.9) можна записати у вигляді |
|
||||||||||||||
|
|
1 |
|
|
σ1 −σ2 |
−tgϕ |
σ1 +σ2 |
= c . |
(8.10) |
||||||
|
cosϕ |
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||
Цю формулу широко застосовують у задачах теорії граничної рівноваги. Якщо з’єднати точку дотику граничної прямої ОЕ з кінцем відрізка σ2 (точка А на рис. 8.1, в), то напрям ЕА визначить напрям площадки ковзання. З
рис. 8.1, в видно, що
BCE = 2β = 90°+ϕ ,
звідки
β = 45°+ϕ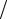 2 .
2 .
Таким чином, в умовах граничної рівноваги площадки ковзання будуть нахилені під кутом ±(45°+φ/2) до напряму площадки найбільшої головної напруги, або, що те ж саме, під кутом ±(45°-φ/2) до напряму головної напруги σ1.
Розглянемо диференціальні рівняння рівноваги ґрунтів у гранично напруженому стані для випадку плоскої задачі. Як відомо з теорії пружності, для цього випадку диференціальні рівняння рівноваги лінійно деформівних тіл при горизонтальній обмежуючій напівпростір площині (напрям осі y – горизонтальний, z – вертикальний) записують у такому вигляді:
∂σ y |
+ |
∂τ yz |
= 0 |
|
|
∂y |
∂z |
|
|||
|
, |
(8.11) |
|||
∂σ z |
|
∂τzy |
|
||
+ |
= γ |
|
|||
∂z |
∂y |
|
|||
|
|
|
|||
де σy, σz, τyz=τzy – складові напруг; γ – питома вага ґрунту.
У цих двох рівняннях три невідомих (σy, σz, τyz), тобто без додаткових умов задача статично не визначена.
Запишемо додаткове рівняння граничної рівноваги, замінивши у формулі (8.10) головні напруги σ1, σ2, виразами їх складових напруг
(σ |
z |
−σ |
y |
)2 + 4τ 2 |
|
|
|
|
|
yz |
= sin2 ϕ . |
(8.12) |
|||
(σ z +σ y + 2c ctgϕ )2 |
|||||||
|
|
||||||
З урахуванням цієї умови задача стає статично визначеною.
` |
188 |
