
- •Preface
- •Acknowledgements
- •Contents
- •2.1 Introduction and a Short History of Black Holes
- •2.2 The Kruskal Extension of Schwarzschild Space-Time
- •2.2.1 Analysis of the Rindler Space-Time
- •2.2.2 Applying the Same Procedure to the Schwarzschild Metric
- •2.2.3 A First Analysis of Kruskal Space-Time
- •2.3 Basic Concepts about Future, Past and Causality
- •2.3.1 The Light-Cone
- •2.3.2 Future and Past of Events and Regions
- •Achronal Sets
- •Time-Orientability
- •Domains of Dependence
- •Cauchy surfaces
- •2.4.1 Conformal Mapping of Minkowski Space into the Einstein Static Universe
- •2.4.2 Asymptotic Flatness
- •2.5 The Causal Boundary of Kruskal Space-Time
- •References
- •3.1 Introduction
- •3.2 The Kerr-Newman Metric
- •3.2.1 Riemann and Ricci Curvatures of the Kerr-Newman Metric
- •3.3 The Static Limit in Kerr-Newman Space-Time
- •Static Observers
- •3.4 The Horizon and the Ergosphere
- •The Horizon Area
- •3.5 Geodesics of the Kerr Metric
- •3.5.2 The Hamilton-Jacobi Equation and the Carter Constant
- •3.5.3 Reduction to First Order Equations
- •3.5.4 The Exact Solution of the Schwarzschild Orbit Equation as an Application
- •3.5.5 About Explicit Kerr Geodesics
- •3.6 The Kerr Black Hole and the Laws of Thermodynamics
- •3.6.1 The Penrose Mechanism
- •3.6.2 The Bekenstein Hawking Entropy and Hawking Radiation
- •References
- •4.1 Historical Introduction to Modern Cosmology
- •4.2 The Universe Is a Dynamical System
- •4.3 Expansion of the Universe
- •4.3.1 Why the Night is Dark and Olbers Paradox
- •4.3.2 Hubble, the Galaxies and the Great Debate
- •4.3.4 The Big Bang
- •4.4 The Cosmological Principle
- •4.5 The Cosmic Background Radiation
- •4.6 The New Scenario of the Inflationary Universe
- •4.7 The End of the Second Millennium and the Dawn of the Third Bring Great News in Cosmology
- •References
- •5.1 Introduction
- •5.2 Mathematical Interlude: Isometries and the Geometry of Coset Manifolds
- •5.2.1 Isometries and Killing Vector Fields
- •5.2.2 Coset Manifolds
- •5.2.3 The Geometry of Coset Manifolds
- •5.2.3.1 Infinitesimal Transformations and Killing Vectors
- •5.2.3.2 Vielbeins, Connections and Metrics on G/H
- •5.2.3.3 Lie Derivatives
- •5.2.3.4 Invariant Metrics on Coset Manifolds
- •5.2.3.5 For Spheres and Pseudo-Spheres
- •5.3 Homogeneity Without Isotropy: What Might Happen
- •5.3.1 Bianchi Spaces and Kasner Metrics
- •5.3.1.1 Bianchi Type I and Kasner Metrics
- •5.3.2.1 A Ricci Flat Bianchi II Metric
- •5.3.3 Einstein Equation and Matter for This Billiard
- •5.3.4 The Same Billiard with Some Matter Content
- •5.3.5 Three-Space Geometry of This Toy Model
- •5.4 The Standard Cosmological Model: Isotropic and Homogeneous Metrics
- •5.4.1 Viewing the Coset Manifolds as Group Manifolds
- •5.5 Friedman Equations for the Scale Factor and the Equation of State
- •5.5.1 Proof of the Cosmological Red-Shift
- •5.5.2 Solution of the Cosmological Differential Equations for Dust and Radiation Without a Cosmological Constant
- •5.5.3 Embedding Cosmologies into de Sitter Space
- •5.6 General Consequences of Friedman Equations
- •5.6.1 Particle Horizon
- •5.6.2 Event Horizon
- •5.6.3 Red-Shift Distances
- •5.7 Conceptual Problems of the Standard Cosmological Model
- •5.8 Cosmic Evolution with a Scalar Field: The Basis for Inflation
- •5.8.1 de Sitter Solution
- •5.8.2 Slow-Rolling Approximate Solutions
- •5.8.2.1 Number of e-Folds
- •5.9 Primordial Perturbations of the Cosmological Metric and of the Inflaton
- •5.9.1 The Conformal Frame
- •5.9.2 Deriving the Equations for the Perturbation
- •5.9.2.1 Meaning of the Propagation Equation
- •5.9.2.2 Evaluation of the Effective Mass Term in the Slow Roll Approximation
- •5.9.2.3 Derivation of the Propagation Equation
- •5.9.3 Quantization of the Scalar Degree of Freedom
- •5.9.4 Calculation of the Power Spectrum in the Two Regimes
- •5.9.4.1 Short Wave-Lengths
- •5.9.4.2 Long Wave-Lengths
- •5.9.4.3 Gluing the Long and Short Wave-Length Solutions Together
- •5.9.4.4 The Spectral Index
- •5.10 The Anisotropies of the Cosmic Microwave Background
- •5.10.1 The Sachs-Wolfe Effect
- •5.10.2 The Two-Point Temperature Correlation Function
- •5.10.3 Conclusive Remarks on CMB Anisotropies
- •References
- •6.1 Historical Outline and Introduction
- •6.1.1 Fermionic Strings and the Birth of Supersymmetry
- •6.1.2 Supersymmetry
- •6.1.3 Supergravity
- •6.2 Algebro-Geometric Structure of Supergravity
- •6.3 Free Differential Algebras
- •6.3.1 Chevalley Cohomology
- •Contraction and Lie Derivative
- •Definition of FDA
- •Classification of FDA and the Analogue of Levi Theorem: Minimal Versus Contractible Algebras
- •6.4 The Super FDA of M Theory and Its Cohomological Structure
- •6.4.1 The Minimal FDA of M-Theory and Cohomology
- •6.4.2 FDA Equivalence with Larger (Super) Lie Algebras
- •6.5 The Principle of Rheonomy
- •6.5.1 The Flow Chart for the Construction of a Supergravity Theory
- •6.6 Summary of Supergravities
- •Type IIA Super-Poicaré Algebra in the String Frame
- •The FDA Extension of the Type IIA Superalgebra in the String Frame
- •The Bianchi Identities
- •6.7.1 Rheonomic Parameterizations of the Type IIA Curvatures in the String Frame
- •Bosonic Curvatures
- •Fermionic Curvatures
- •6.7.2 Field Equations of Type IIA Supergravity in the String Frame
- •6.8 Type IIB Supergravity
- •SL(2, R) Lie Algebra
- •Coset Representative of SL(2, R)/O(2) in the Solvable Parameterization
- •The SU(1, 1)/U(1) Vielbein and Connection
- •6.8.2 The Free Differential Algebra, the Supergravity Fields and the Curvatures
- •The Curvatures of the Free Differential Algebra in the Complex Basis
- •The Curvatures of the Free Differential Algebra in the Real Basis
- •6.8.3 The Bosonic Field Equations and the Standard Form of the Bosonic Action
- •6.9 About Solutions
- •References
- •7.1 Introduction and Conceptual Outline
- •7.2 p-Branes as World Volume Gauge-Theories
- •7.4 The New First Order Formalism
- •7.4.1 An Alternative to the Polyakov Action for p-Branes
- •7.6 The D3-Brane: Summary
- •7.9 Domain Walls in Diverse Space-Time Dimensions
- •7.9.1 The Randall Sundrum Mechanism
- •7.9.2 The Conformal Gauge for Domain Walls
- •7.10 Conclusion on This Brane Bestiary
- •References
- •8.1 Introduction
- •8.2 Supergravity and Homogeneous Scalar Manifolds G/H
- •8.2.3 Scalar Manifolds of Maximal Supergravities in Diverse Dimensions
- •8.3 Duality Symmetries in Even Dimensions
- •8.3.1 The Kinetic Matrix N and Symplectic Embeddings
- •8.3.2 Symplectic Embeddings in General
- •8.5 Summary of Special Kähler Geometry
- •8.5.1 Hodge-Kähler Manifolds
- •8.5.2 Connection on the Line Bundle
- •8.5.3 Special Kähler Manifolds
- •8.6 Supergravities in Five Dimension and More Scalar Geometries
- •8.6.1 Very Special Geometry
- •8.6.3 Quaternionic Geometry
- •8.6.4 Quaternionic, Versus HyperKähler Manifolds
- •References
- •9.1 Introduction
- •9.2 Black Holes Once Again
- •9.2.2 The Oxidation Rules
- •Orbit of Solutions
- •The Schwarzschild Case
- •The Extremal Reissner Nordström Case
- •Curvature of the Extremal Spaces
- •9.2.4 Attractor Mechanism, the Entropy and Other Special Geometry Invariants
- •9.2.5 Critical Points of the Geodesic Potential and Attractors
- •At BPS Attractor Points
- •At Non-BPS Attractor Points of Type I
- •At Non-BPS Attractor Points of Type II
- •9.2.6.2 The Quartic Invariant
- •9.2.7.1 An Explicit Example of Exact Regular BPS Solution
- •The Metric
- •The Scalar Field
- •The Electromagnetic Fields
- •The Fixed Scalars at Horizon and the Entropy
- •The Metric
- •The Scalar Field
- •The Electromagnetic Fields
- •The Fixed Scalars at Horizon and the Entropy
- •9.2.9 Resuming the Discussion of Critical Points
- •Non-BPS Case
- •BPS Case
- •9.2.10 An Example of a Small Black Hole
- •The Metric
- •The Complex Scalar Field
- •The Electromagnetic Fields
- •The Charges
- •Structure of the Charges and Attractor Mechanism
- •9.2.11 Behavior of the Riemann Tensor in Regular Solutions
- •9.3.4 The SO(8) Spinor Bundle and the Holonomy Tensor
- •9.3.5 The Well Adapted Basis of Gamma Matrices
- •9.3.6 The so(8)-Connection and the Holonomy Tensor
- •9.3.7 The Holonomy Tensor and Superspace
- •9.3.8 Gauged Maurer Cartan 1-Forms of OSp(8|4)
- •9.3.9 Killing Spinors of the AdS4 Manifold
- •9.3.10 Supergauge Completion in Mini Superspace
- •9.3.11 The 3-Form
- •9.4.1 Maurer Cartan Forms of OSp(6|4)
- •9.4.2 Explicit Construction of the P3 Geometry
- •9.4.3 The Compactification Ansatz
- •9.4.4 Killing Spinors on P3
- •9.4.5 Gauge Completion in Mini Superspace
- •9.4.6 Gauge Completion of the B[2] Form
- •9.5 Conclusions
- •References
- •10.1 The Legacy of Volume 1
- •10.2 The Story Told in Volume 2
- •Appendix A: Spinors and Gamma Matrix Algebra
- •A.2 The Clifford Algebra
- •A.2.1 Even Dimensions
- •A.2.2 Odd Dimensions
- •A.3 The Charge Conjugation Matrix
- •A.4 Majorana, Weyl and Majorana-Weyl Spinors
- •Appendix B: Auxiliary Tools for p-Brane Actions
- •B.1 Notations and Conventions
- •Appendix C: Auxiliary Information About Some Superalgebras
- •C.1.1 The Superalgebra
- •C.2 The Relevant Supercosets and Their Relation
- •C.2.1 Finite Supergroup Elements
- •C.4 An so(6) Inversion Formula
- •Appendix D: MATHEMATICA Package NOVAMANIFOLDA
- •Coset Manifolds (Euclidian Signature)
- •Instructions for the Use
- •Description of the Main Commands of RUNCOSET
- •Structure Constants for CP2
- •Spheres
- •N010 Coset
- •RUNCOSET Package (Euclidian Signature)
- •Main
- •Spin Connection and Curvature Routines
- •Routine Curvapack
- •Routine Curvapackgen
- •Contorsion Routine for Mixed Vielbeins
- •Calculation of the Contorsion for General Manifolds
- •Calculation for Cartan Maurer Equations and Vielbein Differentials (Euclidian Signature)
- •Routine Thoft
- •AdS Space in Four Dimensions (Minkowski Signature)
- •Lie Algebra of SO(2, 3) and Killing Metric
- •Solvable Subalgebra Generating the Coset and Construction of the Vielbein
- •Killing Vectors
- •Trigonometric Coordinates
- •Test of Killing Vectors
- •MANIFOLDPROVA
- •The 4-Dimensional Coset CP2
- •Calculation of the (Pseudo-)Riemannian Geometry of a Kasner Metric in Vielbein Formalism
- •References
- •Index
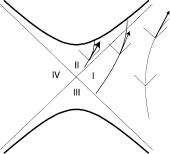
2.3 Basic Concepts about Future, Past and Causality |
19 |
Fig. 2.9 The light-cone orientations in Kruskal space-time and the difference between physical geodesics in regions I and II
its inclination α with respect to the X axis is in the following range 3π/4 ≥ α ≥ π/4. This applies to the whole plane, yet it implies a fundamental difference in the destiny of physical particles that start their journey in region I (or IV) of the Kruskal plane, with respect to the destiny of those ones that happen to be in region II at some point of their life. As it is visually evident from Fig. 2.9, in region I we can have curves (and in particular geodesics) whose tangent vector is time-like and future oriented at any of their points which nonetheless avoid the singular locus and escape to infinity. In the same region there are also future oriented time-like curves which cross the horizon X = ±T and end up on the singular locus, yet these are not the only ones, as already remarked. On the contrary all curves that at some point happen to be inside region II can no longer escape to infinity since, in order to be able to do so, their tangent vector should be space-like, at least at some of their points. Hence the horizon can be crossed from region I to region II, never in the opposite direction. This leads to the existence of a Black-Hole, namely a space-time region, (II in our case) where gravity is so strong that not even light can escape from it. No signal from region II can reach a distant observer located in region I who therefore perceives only the presence of the gravitational field of the black hole swapping infalling matter.
To encode the ideas intuitively described in this section into a rigorous mathematical framework we proceed next to implement our already announced programme. This is the critical review of the concepts of Future, Past and Causality within General Relativity, namely when we assume that all physical events are points p in a pseudo-Riemannian manifold (M , g) with a Lorentzian signature.
2.3 Basic Concepts about Future, Past and Causality
Our discussion starts by reviewing the basic properties of the light-cone (see Fig. 2.10). In Special Relativity, where space-time is Minkowski-space, namely a pseudo-Riemannian manifold which is also affine, the light cone has a global meaning, while in General Relativity light-cones can be defined only locally, namely at each point p M . In any case the Lorentzian signature of the metric implies thatp M , the tangent space Tp M is isomorphic to Minkowski space and it admits the same decomposition in time-like, null-like and space-like sub-manifolds. Hence

20 |
2 Extended Space-Times, Causal Structure and Penrose Diagrams |
Fig. 2.10 The structure of the light-cone
the analysis of the light-cone properties has a general meaning also in General Relativity, although such analysis needs to be repeated at each point. All the complexities inherent with the notion of global causality arise from the need of gluing together the locally defined light-cones. We will develop appropriate conceptual tools to manage such a gluing after our review of the local light-cone properties.
2.3.1 The Light-Cone
When a metric has a Lorentzian signature, vectors t can be of three-types:
1.Time-like, if (t, t) < 0 in mostly plus convention for gμν .
2.Space-like, if (t, t) > 0 in mostly plus convention for gμν .
3.Null-like, if (t, t) = 0 both in mostly plus and mostly minus convention for gμν .
At any point p M the light-cone Cp is composed by the set of vectors t Tp M which are either time-like or null-like. In order to study the properties of the lightcones it is convenient to review a few elementary but basic properties of vectors in Minkowski space.
Theorem 2.3.1 All vectors orthogonal to a time-like vector are space-like.
Proof Using a mostly plus signature, we can go to a diagonal basis such that:
g(X, Y ) = g00X0Y 0 + (X, Y) |
(2.3.1) |
where g00 < 0 and ( , ) denotes a non-degenerate, positive-definite, Euclidian bilin- |
|||||||||
ear form on Rn−1. In this basis, if X T and T is time-like we have: |
|
||||||||
−g00T 0T 0 > (T, T) |
(2.3.2) |
||||||||
−g00T 0X0 = (T, X) ≤ √ |
|
|
|
|
|||||
(T, T)(X, X) |
|
||||||||
Then we get: |
|
|
|
|
|
|
|
||
|
|
g00T 0X0 |
|
(T, X) |
|
||||
|
− |
< |
√(T, T) |
≤ (X, X) |
(2.3.3) |
||||
|
g00T 0T 0 |
||||||||
− |
|
|
|
|
|
|
|
||
2.3 Basic Concepts about Future, Past and Causality |
21 |
Squaring all terms in (2.3.3) we obtain |
|
−g00X0X0 < (X, X) g(X, X) > 0 |
(2.3.4) |
namely the four-vector X is space-like as asserted by the theorem. |
|
Another useful property is given by the following |
|
Lemma 2.3.1 The sum of two future-directed time-like vectors is a future-directed time-like vector.
Proof Let t and T be the two vectors under considerations. By hypothesis we have
|
|
|
|
g(t, t) < 0; |
t0 > 0 |
(2.3.5) |
||||
|
|
|
g(T , T ) < 0; |
T 0 > 0 |
|
|||||
Since: |
|
|
|
|||||||
|
√ |
|
|
|
t0 > (t, t) |
|
|
|
||
−g00 |
|
|
|
|||||||
√ |
|
|
T 0 > (T, T) |
|
|
(2.3.6) |
||||
−g00 |
|
|
||||||||
√ |
|
t0T 0 > √ |
|
> (t, T) |
|
|||||
−g00 |
(t, t)(T, T) |
|
||||||||
we have: |
|
|
|
|||||||
g(t + T , t + T ) = g(t, t) + g(T , T ) + 2g(t, T ) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
(2.3.7) |
−g00 t0 2 + T 0 2 + 2t0T 0 > (t, t) + (T, T) + 2(t, T) |
|
|||||||||
which proves that t + T is time-like. Moreover t0 + T 0 > 0 and so the sum vector is also future-directed as advocated by the lemma.
On the other hand with obvious changes in the proof of Theorem 2.3.1 the following lemma is established
Lemma 2.3.2 All vectors X, orthogonal to a light-like vector L are either light-like or space-like.
Let us now consider in the manifold (M , g) surfaces Σ defined by the vanishing of some smooth function of the local coordinates:
p Σ f (p) = 0 where f C∞(M ) |
(2.3.8) |
By definition the normal vector to the surface Σ is the gradient of the function f :
nμ(Σ) = μf = ∂μf |
(2.3.9) |
