
- •Preface
- •Acknowledgements
- •Contents
- •2.1 Introduction and a Short History of Black Holes
- •2.2 The Kruskal Extension of Schwarzschild Space-Time
- •2.2.1 Analysis of the Rindler Space-Time
- •2.2.2 Applying the Same Procedure to the Schwarzschild Metric
- •2.2.3 A First Analysis of Kruskal Space-Time
- •2.3 Basic Concepts about Future, Past and Causality
- •2.3.1 The Light-Cone
- •2.3.2 Future and Past of Events and Regions
- •Achronal Sets
- •Time-Orientability
- •Domains of Dependence
- •Cauchy surfaces
- •2.4.1 Conformal Mapping of Minkowski Space into the Einstein Static Universe
- •2.4.2 Asymptotic Flatness
- •2.5 The Causal Boundary of Kruskal Space-Time
- •References
- •3.1 Introduction
- •3.2 The Kerr-Newman Metric
- •3.2.1 Riemann and Ricci Curvatures of the Kerr-Newman Metric
- •3.3 The Static Limit in Kerr-Newman Space-Time
- •Static Observers
- •3.4 The Horizon and the Ergosphere
- •The Horizon Area
- •3.5 Geodesics of the Kerr Metric
- •3.5.2 The Hamilton-Jacobi Equation and the Carter Constant
- •3.5.3 Reduction to First Order Equations
- •3.5.4 The Exact Solution of the Schwarzschild Orbit Equation as an Application
- •3.5.5 About Explicit Kerr Geodesics
- •3.6 The Kerr Black Hole and the Laws of Thermodynamics
- •3.6.1 The Penrose Mechanism
- •3.6.2 The Bekenstein Hawking Entropy and Hawking Radiation
- •References
- •4.1 Historical Introduction to Modern Cosmology
- •4.2 The Universe Is a Dynamical System
- •4.3 Expansion of the Universe
- •4.3.1 Why the Night is Dark and Olbers Paradox
- •4.3.2 Hubble, the Galaxies and the Great Debate
- •4.3.4 The Big Bang
- •4.4 The Cosmological Principle
- •4.5 The Cosmic Background Radiation
- •4.6 The New Scenario of the Inflationary Universe
- •4.7 The End of the Second Millennium and the Dawn of the Third Bring Great News in Cosmology
- •References
- •5.1 Introduction
- •5.2 Mathematical Interlude: Isometries and the Geometry of Coset Manifolds
- •5.2.1 Isometries and Killing Vector Fields
- •5.2.2 Coset Manifolds
- •5.2.3 The Geometry of Coset Manifolds
- •5.2.3.1 Infinitesimal Transformations and Killing Vectors
- •5.2.3.2 Vielbeins, Connections and Metrics on G/H
- •5.2.3.3 Lie Derivatives
- •5.2.3.4 Invariant Metrics on Coset Manifolds
- •5.2.3.5 For Spheres and Pseudo-Spheres
- •5.3 Homogeneity Without Isotropy: What Might Happen
- •5.3.1 Bianchi Spaces and Kasner Metrics
- •5.3.1.1 Bianchi Type I and Kasner Metrics
- •5.3.2.1 A Ricci Flat Bianchi II Metric
- •5.3.3 Einstein Equation and Matter for This Billiard
- •5.3.4 The Same Billiard with Some Matter Content
- •5.3.5 Three-Space Geometry of This Toy Model
- •5.4 The Standard Cosmological Model: Isotropic and Homogeneous Metrics
- •5.4.1 Viewing the Coset Manifolds as Group Manifolds
- •5.5 Friedman Equations for the Scale Factor and the Equation of State
- •5.5.1 Proof of the Cosmological Red-Shift
- •5.5.2 Solution of the Cosmological Differential Equations for Dust and Radiation Without a Cosmological Constant
- •5.5.3 Embedding Cosmologies into de Sitter Space
- •5.6 General Consequences of Friedman Equations
- •5.6.1 Particle Horizon
- •5.6.2 Event Horizon
- •5.6.3 Red-Shift Distances
- •5.7 Conceptual Problems of the Standard Cosmological Model
- •5.8 Cosmic Evolution with a Scalar Field: The Basis for Inflation
- •5.8.1 de Sitter Solution
- •5.8.2 Slow-Rolling Approximate Solutions
- •5.8.2.1 Number of e-Folds
- •5.9 Primordial Perturbations of the Cosmological Metric and of the Inflaton
- •5.9.1 The Conformal Frame
- •5.9.2 Deriving the Equations for the Perturbation
- •5.9.2.1 Meaning of the Propagation Equation
- •5.9.2.2 Evaluation of the Effective Mass Term in the Slow Roll Approximation
- •5.9.2.3 Derivation of the Propagation Equation
- •5.9.3 Quantization of the Scalar Degree of Freedom
- •5.9.4 Calculation of the Power Spectrum in the Two Regimes
- •5.9.4.1 Short Wave-Lengths
- •5.9.4.2 Long Wave-Lengths
- •5.9.4.3 Gluing the Long and Short Wave-Length Solutions Together
- •5.9.4.4 The Spectral Index
- •5.10 The Anisotropies of the Cosmic Microwave Background
- •5.10.1 The Sachs-Wolfe Effect
- •5.10.2 The Two-Point Temperature Correlation Function
- •5.10.3 Conclusive Remarks on CMB Anisotropies
- •References
- •6.1 Historical Outline and Introduction
- •6.1.1 Fermionic Strings and the Birth of Supersymmetry
- •6.1.2 Supersymmetry
- •6.1.3 Supergravity
- •6.2 Algebro-Geometric Structure of Supergravity
- •6.3 Free Differential Algebras
- •6.3.1 Chevalley Cohomology
- •Contraction and Lie Derivative
- •Definition of FDA
- •Classification of FDA and the Analogue of Levi Theorem: Minimal Versus Contractible Algebras
- •6.4 The Super FDA of M Theory and Its Cohomological Structure
- •6.4.1 The Minimal FDA of M-Theory and Cohomology
- •6.4.2 FDA Equivalence with Larger (Super) Lie Algebras
- •6.5 The Principle of Rheonomy
- •6.5.1 The Flow Chart for the Construction of a Supergravity Theory
- •6.6 Summary of Supergravities
- •Type IIA Super-Poicaré Algebra in the String Frame
- •The FDA Extension of the Type IIA Superalgebra in the String Frame
- •The Bianchi Identities
- •6.7.1 Rheonomic Parameterizations of the Type IIA Curvatures in the String Frame
- •Bosonic Curvatures
- •Fermionic Curvatures
- •6.7.2 Field Equations of Type IIA Supergravity in the String Frame
- •6.8 Type IIB Supergravity
- •SL(2, R) Lie Algebra
- •Coset Representative of SL(2, R)/O(2) in the Solvable Parameterization
- •The SU(1, 1)/U(1) Vielbein and Connection
- •6.8.2 The Free Differential Algebra, the Supergravity Fields and the Curvatures
- •The Curvatures of the Free Differential Algebra in the Complex Basis
- •The Curvatures of the Free Differential Algebra in the Real Basis
- •6.8.3 The Bosonic Field Equations and the Standard Form of the Bosonic Action
- •6.9 About Solutions
- •References
- •7.1 Introduction and Conceptual Outline
- •7.2 p-Branes as World Volume Gauge-Theories
- •7.4 The New First Order Formalism
- •7.4.1 An Alternative to the Polyakov Action for p-Branes
- •7.6 The D3-Brane: Summary
- •7.9 Domain Walls in Diverse Space-Time Dimensions
- •7.9.1 The Randall Sundrum Mechanism
- •7.9.2 The Conformal Gauge for Domain Walls
- •7.10 Conclusion on This Brane Bestiary
- •References
- •8.1 Introduction
- •8.2 Supergravity and Homogeneous Scalar Manifolds G/H
- •8.2.3 Scalar Manifolds of Maximal Supergravities in Diverse Dimensions
- •8.3 Duality Symmetries in Even Dimensions
- •8.3.1 The Kinetic Matrix N and Symplectic Embeddings
- •8.3.2 Symplectic Embeddings in General
- •8.5 Summary of Special Kähler Geometry
- •8.5.1 Hodge-Kähler Manifolds
- •8.5.2 Connection on the Line Bundle
- •8.5.3 Special Kähler Manifolds
- •8.6 Supergravities in Five Dimension and More Scalar Geometries
- •8.6.1 Very Special Geometry
- •8.6.3 Quaternionic Geometry
- •8.6.4 Quaternionic, Versus HyperKähler Manifolds
- •References
- •9.1 Introduction
- •9.2 Black Holes Once Again
- •9.2.2 The Oxidation Rules
- •Orbit of Solutions
- •The Schwarzschild Case
- •The Extremal Reissner Nordström Case
- •Curvature of the Extremal Spaces
- •9.2.4 Attractor Mechanism, the Entropy and Other Special Geometry Invariants
- •9.2.5 Critical Points of the Geodesic Potential and Attractors
- •At BPS Attractor Points
- •At Non-BPS Attractor Points of Type I
- •At Non-BPS Attractor Points of Type II
- •9.2.6.2 The Quartic Invariant
- •9.2.7.1 An Explicit Example of Exact Regular BPS Solution
- •The Metric
- •The Scalar Field
- •The Electromagnetic Fields
- •The Fixed Scalars at Horizon and the Entropy
- •The Metric
- •The Scalar Field
- •The Electromagnetic Fields
- •The Fixed Scalars at Horizon and the Entropy
- •9.2.9 Resuming the Discussion of Critical Points
- •Non-BPS Case
- •BPS Case
- •9.2.10 An Example of a Small Black Hole
- •The Metric
- •The Complex Scalar Field
- •The Electromagnetic Fields
- •The Charges
- •Structure of the Charges and Attractor Mechanism
- •9.2.11 Behavior of the Riemann Tensor in Regular Solutions
- •9.3.4 The SO(8) Spinor Bundle and the Holonomy Tensor
- •9.3.5 The Well Adapted Basis of Gamma Matrices
- •9.3.6 The so(8)-Connection and the Holonomy Tensor
- •9.3.7 The Holonomy Tensor and Superspace
- •9.3.8 Gauged Maurer Cartan 1-Forms of OSp(8|4)
- •9.3.9 Killing Spinors of the AdS4 Manifold
- •9.3.10 Supergauge Completion in Mini Superspace
- •9.3.11 The 3-Form
- •9.4.1 Maurer Cartan Forms of OSp(6|4)
- •9.4.2 Explicit Construction of the P3 Geometry
- •9.4.3 The Compactification Ansatz
- •9.4.4 Killing Spinors on P3
- •9.4.5 Gauge Completion in Mini Superspace
- •9.4.6 Gauge Completion of the B[2] Form
- •9.5 Conclusions
- •References
- •10.1 The Legacy of Volume 1
- •10.2 The Story Told in Volume 2
- •Appendix A: Spinors and Gamma Matrix Algebra
- •A.2 The Clifford Algebra
- •A.2.1 Even Dimensions
- •A.2.2 Odd Dimensions
- •A.3 The Charge Conjugation Matrix
- •A.4 Majorana, Weyl and Majorana-Weyl Spinors
- •Appendix B: Auxiliary Tools for p-Brane Actions
- •B.1 Notations and Conventions
- •Appendix C: Auxiliary Information About Some Superalgebras
- •C.1.1 The Superalgebra
- •C.2 The Relevant Supercosets and Their Relation
- •C.2.1 Finite Supergroup Elements
- •C.4 An so(6) Inversion Formula
- •Appendix D: MATHEMATICA Package NOVAMANIFOLDA
- •Coset Manifolds (Euclidian Signature)
- •Instructions for the Use
- •Description of the Main Commands of RUNCOSET
- •Structure Constants for CP2
- •Spheres
- •N010 Coset
- •RUNCOSET Package (Euclidian Signature)
- •Main
- •Spin Connection and Curvature Routines
- •Routine Curvapack
- •Routine Curvapackgen
- •Contorsion Routine for Mixed Vielbeins
- •Calculation of the Contorsion for General Manifolds
- •Calculation for Cartan Maurer Equations and Vielbein Differentials (Euclidian Signature)
- •Routine Thoft
- •AdS Space in Four Dimensions (Minkowski Signature)
- •Lie Algebra of SO(2, 3) and Killing Metric
- •Solvable Subalgebra Generating the Coset and Construction of the Vielbein
- •Killing Vectors
- •Trigonometric Coordinates
- •Test of Killing Vectors
- •MANIFOLDPROVA
- •The 4-Dimensional Coset CP2
- •Calculation of the (Pseudo-)Riemannian Geometry of a Kasner Metric in Vielbein Formalism
- •References
- •Index

154 |
5 Cosmology and General Relativity |
space-time is homogeneous. In addition we need the same scale factor a(t) in all directions and this is the outcome of isotropy.
5.5.2Solution of the Cosmological Differential Equations for Dust and Radiation Without a Cosmological Constant
If we substitute the first integral given by the conservation law (5.5.3) into the first of the differential equations (5.4.12) we get:
a |
|
|
|
Cd |
|
|
|
|
|
κ |
|
|
|
|
||||
3( a˙ )2 = |
|
|
|
|
− 3 |
|
|
|
; |
dust |
|
|||||||
a3 |
a2 |
(5.5.18) |
||||||||||||||||
a |
2 |
|
|
Cr |
|
|
|
|
κ |
|
|
|
|
|||||
3( a˙ ) |
|
= |
|
|
|
− 3 |
|
|
|
; |
radiation |
|
||||||
|
a4 |
a2 |
|
|||||||||||||||
where we have defined: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8π G |
|
(5.5.19) |
||||||
|
|
|
Cd |
|
|
|
|
|
|
|
|
Cd |
|
|||||
|
|
|
|
3 |
|
|
|
|
||||||||||
|
|
|
|
r = |
|
|
|
7r |
|
|
||||||||
Equations (5.5.18) are easily reduced to quadratures obtaining: |
|
|||||||||||||||||
dadt |
|
|
|
|
|
|
|
|
||||||||||
= |
Cad |
− κ; |
|
dust |
(5.5.20) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
da |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Cr |
|
− κ; |
|
radiation |
|
|||||||||
dt |
= a2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The differential equation for the scale factor in the case of a radiation filled universe is immediately integrated and yields the following simple result:
|
|
|
2√ |
|
t − t2 |
for κ = 1 |
|
|
||||||
|
|
Cr |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
− |
|
|
|
|
|
= − |
|
|
|
a(t) |
|
|
|
t2 |
|
|
2√ |
Cr |
t |
for κ |
|
1 |
(5.5.21) |
|
|
|
|
√2√Cr √t |
for κ = 0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
where the integration constant has been fixed by means of the boundary condition a(0) = 0 (see Fig. 5.17).
As it is evident from the above analytic form the solution for a positively curved
√
universe (κ = 1) makes sense only in the interval, 0 ≤ t ≤ 2 Cr where the function under square root is positive. Hence while for the open and flat universe (κ ≤ 0), the scale factor grows indefinitely and the expansion never ceases, the closed universe undergoes an expansion phase followed by a contraction one which finally concentrates again all the radiation into a single point with a diverging energy density.
Although the analytic form of the solution is slightly different, the qualitative behavior of the scale factor follows exactly the same pattern also in the case of a dust filled universe, as we demonstrate in the following subsections, separately analyzing the three cases.
5.5 Friedman Equations for the Scale Factor and the Equation of State |
155 |
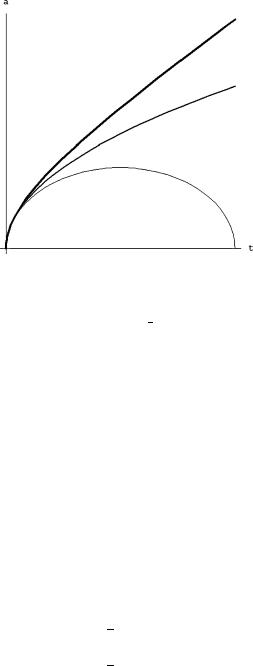
Fig. 5.17 Evolution of the cosmological scale factor a(t) in the case of a radiation filled universe, for the three cases of positive (κ = 1), negative (κ = −1) and vanishing spatial curvature (κ = 0). The thickest line corresponds to the hyperbolic case (κ = −1) where, for late times, the scale factor grows asymptotically as a t . The medium thick line corresponds to the flat case where the late time asymptotic behavior of the scale factor is a √t . Finally the thinnest line correspond to the elliptic case (κ = 1), where the scale factor reaches a maximum and then contracts again to zero
5.5.2.1Parametric Solution in the Dust Case of a Positively Curved Universe κ = 1
We solve the differential equation pertaining to this case by means of a suitable change of variables. We introduce the new variable η and we set:
|
|
|
a = |
1 |
Cd (1 − cos η) |
(5.5.22) |
|||||
|
|
|
2 |
||||||||
Then we immediately get: |
|
|
|
|
|
|
|
||||
dt = |
|
|
da |
|
|
= |
1 |
Cd (1 |
− cos η) dη |
(5.5.23) |
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|||||||
|
Cd |
− 1 |
|||||||||
|
a |
|
|
|
|
|
|||||
and hence, by straightforward integration, we find the parametric solution for the curve describing the evolution of the scale factor in the plane t, a:
a(η) = 1 Cd (1 − cos η)
2
(5.5.24)
t (η) = 1 Cd (η − sin η)
2
In Fig. 5.18 we show two instances of these evolutions. As one sees, in a positively curved universe, an initial expansion is always followed by a contraction phase.

156 |
5 Cosmology and General Relativity |
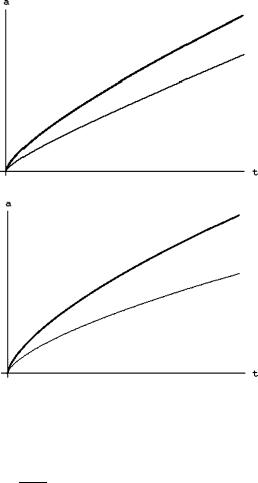
Fig. 5.18 Evolution of the cosmological scale factor a(t) in the case of a closed (κ = 1) dust universe. The amplitude of the expansion, before the contraction sets on, depends on the total matter content of the universe codified by the constant Cd . In the figure we show two cases Cd = 1 (thicker line) and Cd = 0.6 (thinner line)
The amplitude of the expansion before the contraction depends on the total matter content of the universe.
5.5.2.2Parametric Solution in the Dust Case of a Negatively Curved Universe κ = −1
The solution for the hyperbolic universe is obtained in a similar way. Rather than (5.5.22) we pose:
|
1 |
Cd (1 − cosh η) |
|
|||
a = − |
|
(5.5.25) |
||||
2 |
||||||
and, in complete analogy to the previous case, we obtain: |
|
|||||
|
da = |
1 |
Cd sinh η dη |
|
||
|
|
|
||||
|
2 |
(5.5.26) |
||||
|
dt = |
2 Cd (sinh η − η) |
||||
|
|
|
1 |
|
|
|
so that the parametric description of the scale factor evolution is the following one:
a(η) =
t (η) =
1
2 Cd (cosh η − 1)
(5.5.27)
1
2 Cd (sinh η − η)
In this case the universe expands indefinitely and there is no contraction phase. Also here, the rate of the expansion depends on the total matter content of the universe: the bigger it is the faster the universe expands. Examples of this evolution are shown in Fig. 5.19.
5.5 Friedman Equations for the Scale Factor and the Equation of State |
157 |
Fig. 5.19 Evolution of the cosmological scale factor a(t) in the case of an open
(κ = −1) dust universe. Also here the amplitude of the expansion depends on the total matter content of the universe codified by the constant Cd . The thicker line corresponds to the case
Cd = 1 while the thinner line corresponds to the case
Cd = 0.2
Fig. 5.20 Evolution of the cosmological scale factor a(t) in the case of a flat (κ = 0) dust universe. Also here the amplitude of the expansion depends on the total matter content of the universe codified by the constant Cd . The thicker line corresponds to the case Cd = 1 while the thinner line corresponds to the case Cd = 0.5
5.5.2.3 Parametric Solution in the Dust Case of a Spatially Flat Universe κ = 0
In the case of zero spatial curvature, (5.5.20) reduce, for a dust universe, to:
|
|
|
1 |
|
|
|
|
|
|
|
|
|
dt = |
|
|
√a da |
|
||||||
√ |
|
|
(5.5.28) |
||||||||
Cd |
|||||||||||
and hence we find: |
|
|
|
|
|
|
|
|
|
|
|
|
a = |
9 |
4d |
2/3 |
|
|
(5.5.29) |
||||
|
|
t2/3 |
|||||||||
|
|
|
C |
|
|
|
|
|
|
|
|
We conclude that also the flat, dust filled, universe expands indefinitely and the scale
|
raises as a |
|
t2/3 |
(see Fig. 5.20), to be compared with the weaker growth |
|
factor1/2 |
|
|
|
||
a t |
|
of the same flat universe when it is radiation dominated. |
|||
In Fig. 5.21 we have compared the three kinds of behavior of the cosmological scale factor for the positively, negatively curved and flat, dust filled universe.
As one sees the qualitative behavior is exactly the same as in the case of radiation. Such behavior changes dramatically when we consider the case of universes with a positive space-time curvature, in particular the maximally symmetric de Sitter
space.

158 |
5 Cosmology and General Relativity |
Fig. 5.21 Comparison between the three types of dust filled universes. With the same total matter content
Cd = 1 we have plotted the behavior of the scale factor in the three cases of a closed, open and flat universe. The line that goes back to a = 0 is the closed universe κ = 1. Of the two indefinitely growing lines the thinner is the open universe κ = −1, the thicker is the flat universe κ = 0. The flat universe, initially expands faster than the open one, but at later times it is overcome by the open universe whose
scale factor grows faster than t2/3 for t → ∞
Let us explain.
By assuming the cosmological principle, namely homogeneity and isotropy, we have imposed that the metric of space-time, at the scales of interest for cosmology, has a large symmetry, admitting six Killing vectors, three rotational ones closing the so(3) Lie algebra and three translational ones. In the case of positive spatial curvature κ = 1 the six Killing vectors close the so(4) Lie algebra, for negative curvature κ = −1 they close the Lorentz algebra so(1, 3), while for the flat universe they close the Lie algebra of the three dimensional Euclidian group E3.
Yet six is not the maximal number of Killing vectors that we can have in a fourdimensional manifold. The actual value of such maximal number is 10, namely the dimension of the Poincaré Lie algebra, iso(1, 3), but also of the Lie algebra so(1, 4) and so(2, 3). Indeed there are three maximally symmetric pseudoRiemannian manifolds with Lorentzian signature that, respectively, admit the corresponding group of isometries, namely Minkowski space Mink4, de Sitter space dS4 and anti de Sitter space AdS4. It follows that among the various isotropic and homogeneous universes, classified by the behavior of the scale factor a(t), there should be special ones where the six-dimensional isometry algebra is promoted to a ten dimensional one. Clearly imposing the existence of extra Killing vectors puts differential constraints on the scale factor a(t) which eventually will determine it uniquely.
In the next subsection we analyze in detail de Sitter space and we show that, in the framework of its geometry we cam embed all the three types of cosmological metrics (κ = ±1, 0), clearly with different forms of the scale factor a(t). This might seem paradoxical, but it is not. The key point is that the choice of the time t in the three embeddings is different.
