
- •Preface
- •Acknowledgements
- •Contents
- •2.1 Introduction and a Short History of Black Holes
- •2.2 The Kruskal Extension of Schwarzschild Space-Time
- •2.2.1 Analysis of the Rindler Space-Time
- •2.2.2 Applying the Same Procedure to the Schwarzschild Metric
- •2.2.3 A First Analysis of Kruskal Space-Time
- •2.3 Basic Concepts about Future, Past and Causality
- •2.3.1 The Light-Cone
- •2.3.2 Future and Past of Events and Regions
- •Achronal Sets
- •Time-Orientability
- •Domains of Dependence
- •Cauchy surfaces
- •2.4.1 Conformal Mapping of Minkowski Space into the Einstein Static Universe
- •2.4.2 Asymptotic Flatness
- •2.5 The Causal Boundary of Kruskal Space-Time
- •References
- •3.1 Introduction
- •3.2 The Kerr-Newman Metric
- •3.2.1 Riemann and Ricci Curvatures of the Kerr-Newman Metric
- •3.3 The Static Limit in Kerr-Newman Space-Time
- •Static Observers
- •3.4 The Horizon and the Ergosphere
- •The Horizon Area
- •3.5 Geodesics of the Kerr Metric
- •3.5.2 The Hamilton-Jacobi Equation and the Carter Constant
- •3.5.3 Reduction to First Order Equations
- •3.5.4 The Exact Solution of the Schwarzschild Orbit Equation as an Application
- •3.5.5 About Explicit Kerr Geodesics
- •3.6 The Kerr Black Hole and the Laws of Thermodynamics
- •3.6.1 The Penrose Mechanism
- •3.6.2 The Bekenstein Hawking Entropy and Hawking Radiation
- •References
- •4.1 Historical Introduction to Modern Cosmology
- •4.2 The Universe Is a Dynamical System
- •4.3 Expansion of the Universe
- •4.3.1 Why the Night is Dark and Olbers Paradox
- •4.3.2 Hubble, the Galaxies and the Great Debate
- •4.3.4 The Big Bang
- •4.4 The Cosmological Principle
- •4.5 The Cosmic Background Radiation
- •4.6 The New Scenario of the Inflationary Universe
- •4.7 The End of the Second Millennium and the Dawn of the Third Bring Great News in Cosmology
- •References
- •5.1 Introduction
- •5.2 Mathematical Interlude: Isometries and the Geometry of Coset Manifolds
- •5.2.1 Isometries and Killing Vector Fields
- •5.2.2 Coset Manifolds
- •5.2.3 The Geometry of Coset Manifolds
- •5.2.3.1 Infinitesimal Transformations and Killing Vectors
- •5.2.3.2 Vielbeins, Connections and Metrics on G/H
- •5.2.3.3 Lie Derivatives
- •5.2.3.4 Invariant Metrics on Coset Manifolds
- •5.2.3.5 For Spheres and Pseudo-Spheres
- •5.3 Homogeneity Without Isotropy: What Might Happen
- •5.3.1 Bianchi Spaces and Kasner Metrics
- •5.3.1.1 Bianchi Type I and Kasner Metrics
- •5.3.2.1 A Ricci Flat Bianchi II Metric
- •5.3.3 Einstein Equation and Matter for This Billiard
- •5.3.4 The Same Billiard with Some Matter Content
- •5.3.5 Three-Space Geometry of This Toy Model
- •5.4 The Standard Cosmological Model: Isotropic and Homogeneous Metrics
- •5.4.1 Viewing the Coset Manifolds as Group Manifolds
- •5.5 Friedman Equations for the Scale Factor and the Equation of State
- •5.5.1 Proof of the Cosmological Red-Shift
- •5.5.2 Solution of the Cosmological Differential Equations for Dust and Radiation Without a Cosmological Constant
- •5.5.3 Embedding Cosmologies into de Sitter Space
- •5.6 General Consequences of Friedman Equations
- •5.6.1 Particle Horizon
- •5.6.2 Event Horizon
- •5.6.3 Red-Shift Distances
- •5.7 Conceptual Problems of the Standard Cosmological Model
- •5.8 Cosmic Evolution with a Scalar Field: The Basis for Inflation
- •5.8.1 de Sitter Solution
- •5.8.2 Slow-Rolling Approximate Solutions
- •5.8.2.1 Number of e-Folds
- •5.9 Primordial Perturbations of the Cosmological Metric and of the Inflaton
- •5.9.1 The Conformal Frame
- •5.9.2 Deriving the Equations for the Perturbation
- •5.9.2.1 Meaning of the Propagation Equation
- •5.9.2.2 Evaluation of the Effective Mass Term in the Slow Roll Approximation
- •5.9.2.3 Derivation of the Propagation Equation
- •5.9.3 Quantization of the Scalar Degree of Freedom
- •5.9.4 Calculation of the Power Spectrum in the Two Regimes
- •5.9.4.1 Short Wave-Lengths
- •5.9.4.2 Long Wave-Lengths
- •5.9.4.3 Gluing the Long and Short Wave-Length Solutions Together
- •5.9.4.4 The Spectral Index
- •5.10 The Anisotropies of the Cosmic Microwave Background
- •5.10.1 The Sachs-Wolfe Effect
- •5.10.2 The Two-Point Temperature Correlation Function
- •5.10.3 Conclusive Remarks on CMB Anisotropies
- •References
- •6.1 Historical Outline and Introduction
- •6.1.1 Fermionic Strings and the Birth of Supersymmetry
- •6.1.2 Supersymmetry
- •6.1.3 Supergravity
- •6.2 Algebro-Geometric Structure of Supergravity
- •6.3 Free Differential Algebras
- •6.3.1 Chevalley Cohomology
- •Contraction and Lie Derivative
- •Definition of FDA
- •Classification of FDA and the Analogue of Levi Theorem: Minimal Versus Contractible Algebras
- •6.4 The Super FDA of M Theory and Its Cohomological Structure
- •6.4.1 The Minimal FDA of M-Theory and Cohomology
- •6.4.2 FDA Equivalence with Larger (Super) Lie Algebras
- •6.5 The Principle of Rheonomy
- •6.5.1 The Flow Chart for the Construction of a Supergravity Theory
- •6.6 Summary of Supergravities
- •Type IIA Super-Poicaré Algebra in the String Frame
- •The FDA Extension of the Type IIA Superalgebra in the String Frame
- •The Bianchi Identities
- •6.7.1 Rheonomic Parameterizations of the Type IIA Curvatures in the String Frame
- •Bosonic Curvatures
- •Fermionic Curvatures
- •6.7.2 Field Equations of Type IIA Supergravity in the String Frame
- •6.8 Type IIB Supergravity
- •SL(2, R) Lie Algebra
- •Coset Representative of SL(2, R)/O(2) in the Solvable Parameterization
- •The SU(1, 1)/U(1) Vielbein and Connection
- •6.8.2 The Free Differential Algebra, the Supergravity Fields and the Curvatures
- •The Curvatures of the Free Differential Algebra in the Complex Basis
- •The Curvatures of the Free Differential Algebra in the Real Basis
- •6.8.3 The Bosonic Field Equations and the Standard Form of the Bosonic Action
- •6.9 About Solutions
- •References
- •7.1 Introduction and Conceptual Outline
- •7.2 p-Branes as World Volume Gauge-Theories
- •7.4 The New First Order Formalism
- •7.4.1 An Alternative to the Polyakov Action for p-Branes
- •7.6 The D3-Brane: Summary
- •7.9 Domain Walls in Diverse Space-Time Dimensions
- •7.9.1 The Randall Sundrum Mechanism
- •7.9.2 The Conformal Gauge for Domain Walls
- •7.10 Conclusion on This Brane Bestiary
- •References
- •8.1 Introduction
- •8.2 Supergravity and Homogeneous Scalar Manifolds G/H
- •8.2.3 Scalar Manifolds of Maximal Supergravities in Diverse Dimensions
- •8.3 Duality Symmetries in Even Dimensions
- •8.3.1 The Kinetic Matrix N and Symplectic Embeddings
- •8.3.2 Symplectic Embeddings in General
- •8.5 Summary of Special Kähler Geometry
- •8.5.1 Hodge-Kähler Manifolds
- •8.5.2 Connection on the Line Bundle
- •8.5.3 Special Kähler Manifolds
- •8.6 Supergravities in Five Dimension and More Scalar Geometries
- •8.6.1 Very Special Geometry
- •8.6.3 Quaternionic Geometry
- •8.6.4 Quaternionic, Versus HyperKähler Manifolds
- •References
- •9.1 Introduction
- •9.2 Black Holes Once Again
- •9.2.2 The Oxidation Rules
- •Orbit of Solutions
- •The Schwarzschild Case
- •The Extremal Reissner Nordström Case
- •Curvature of the Extremal Spaces
- •9.2.4 Attractor Mechanism, the Entropy and Other Special Geometry Invariants
- •9.2.5 Critical Points of the Geodesic Potential and Attractors
- •At BPS Attractor Points
- •At Non-BPS Attractor Points of Type I
- •At Non-BPS Attractor Points of Type II
- •9.2.6.2 The Quartic Invariant
- •9.2.7.1 An Explicit Example of Exact Regular BPS Solution
- •The Metric
- •The Scalar Field
- •The Electromagnetic Fields
- •The Fixed Scalars at Horizon and the Entropy
- •The Metric
- •The Scalar Field
- •The Electromagnetic Fields
- •The Fixed Scalars at Horizon and the Entropy
- •9.2.9 Resuming the Discussion of Critical Points
- •Non-BPS Case
- •BPS Case
- •9.2.10 An Example of a Small Black Hole
- •The Metric
- •The Complex Scalar Field
- •The Electromagnetic Fields
- •The Charges
- •Structure of the Charges and Attractor Mechanism
- •9.2.11 Behavior of the Riemann Tensor in Regular Solutions
- •9.3.4 The SO(8) Spinor Bundle and the Holonomy Tensor
- •9.3.5 The Well Adapted Basis of Gamma Matrices
- •9.3.6 The so(8)-Connection and the Holonomy Tensor
- •9.3.7 The Holonomy Tensor and Superspace
- •9.3.8 Gauged Maurer Cartan 1-Forms of OSp(8|4)
- •9.3.9 Killing Spinors of the AdS4 Manifold
- •9.3.10 Supergauge Completion in Mini Superspace
- •9.3.11 The 3-Form
- •9.4.1 Maurer Cartan Forms of OSp(6|4)
- •9.4.2 Explicit Construction of the P3 Geometry
- •9.4.3 The Compactification Ansatz
- •9.4.4 Killing Spinors on P3
- •9.4.5 Gauge Completion in Mini Superspace
- •9.4.6 Gauge Completion of the B[2] Form
- •9.5 Conclusions
- •References
- •10.1 The Legacy of Volume 1
- •10.2 The Story Told in Volume 2
- •Appendix A: Spinors and Gamma Matrix Algebra
- •A.2 The Clifford Algebra
- •A.2.1 Even Dimensions
- •A.2.2 Odd Dimensions
- •A.3 The Charge Conjugation Matrix
- •A.4 Majorana, Weyl and Majorana-Weyl Spinors
- •Appendix B: Auxiliary Tools for p-Brane Actions
- •B.1 Notations and Conventions
- •Appendix C: Auxiliary Information About Some Superalgebras
- •C.1.1 The Superalgebra
- •C.2 The Relevant Supercosets and Their Relation
- •C.2.1 Finite Supergroup Elements
- •C.4 An so(6) Inversion Formula
- •Appendix D: MATHEMATICA Package NOVAMANIFOLDA
- •Coset Manifolds (Euclidian Signature)
- •Instructions for the Use
- •Description of the Main Commands of RUNCOSET
- •Structure Constants for CP2
- •Spheres
- •N010 Coset
- •RUNCOSET Package (Euclidian Signature)
- •Main
- •Spin Connection and Curvature Routines
- •Routine Curvapack
- •Routine Curvapackgen
- •Contorsion Routine for Mixed Vielbeins
- •Calculation of the Contorsion for General Manifolds
- •Calculation for Cartan Maurer Equations and Vielbein Differentials (Euclidian Signature)
- •Routine Thoft
- •AdS Space in Four Dimensions (Minkowski Signature)
- •Lie Algebra of SO(2, 3) and Killing Metric
- •Solvable Subalgebra Generating the Coset and Construction of the Vielbein
- •Killing Vectors
- •Trigonometric Coordinates
- •Test of Killing Vectors
- •MANIFOLDPROVA
- •The 4-Dimensional Coset CP2
- •Calculation of the (Pseudo-)Riemannian Geometry of a Kasner Metric in Vielbein Formalism
- •References
- •Index
Chapter 3
Rotating Black Holes and Thermodynamics
Tu vedresti ’l Zodiaco rubecchio
Ancora all’Orse piú stretto rotare
Se non uscisse fuor dal cammin vecchio.
Sí ch’ambo e due hann’un solo orizzon,
E diversi emisperi: . . .
Dante Alighieri (Purgatorio Canto IV, 64)
3.1 Introduction
In this chapter we study in considerable detail the quite intriguing and challenging properties of rotating black-holes encoded in the Kerr-Newman metric which contains only three parameters (m, J, q) corresponding, respectively, to the mass, to the angular momentum and to the charge of the hole. As anticipated in the previous chapter, irrespectively from all the details of its initial structure, a gravitational collapsing body sets down to a final equilibrium state described by the Kerr-Newman metric, which is the unique one, in D = 4, to be static, stationary, axial symmetric and asymptotically flat. The geodesic problem for this metric is still a completely integrable one, since there are enough first integrals, yet the explicit integration is very much laborious because it involves higher transcendental functions and the classification of trajectories turns out very complicated. We will derive the final integration formulae but we will present only a simple example of their application in view of such a complexity. We will instead dwell on the general new properties displayed by rotating black-holes that allow for a mechanism of energy extraction whose features have a surprising analogy with the laws of thermodynamics. Such an analogy is actually only the tip of an iceberg. The horizon area of the black holes behaves as an entropy and this makes it clear that, in a fundamental quantum theory of gravity, black holes must necessarily be endowed with a statistical interpretation in terms of some kind of microstates.
3.2 The Kerr-Newman Metric
Let us consider the standard set up of polar coordinates r, θ , φ for R3 plus the parameter t for time. For the angular variables θ , φ labeling the points of each 2-
P.G. Frè, Gravity, a Geometrical Course, DOI 10.1007/978-94-007-5443-0_3, |
43 |
© Springer Science+Business Media Dordrecht 2013 |
|
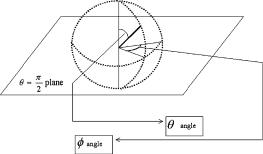
44 |
3 Rotating Black Holes and Thermodynamics |
Fig. 3.1 Our conventions for the angular coordinates on the S2 sphere are as follows: the azimuthal angle φ takes the values in the range [0, 2π ], while the ascension angle θ runs from 0 (the North Pole) to π (the South Pole). The metric ds2 = dθ 2 + sin2 θ dφ2 is singular at θ = 0 and θ = π . These are coordinate singularities that can be removed by redefining θ
sphere of radius r we adopt the same conventions already utilized in establishing the Schwarzschild solution. For reader’s convenience we recall them here in Fig. 3.1.
Using this coordinate patch let us introduce a metric depending on three parameters m, α, q whose physical interpretation will be that of mass, angular momentum and electric/magnetic charge of the black hole, respectively.
It is convenient to introduce the following functions which will play the role of building blocks for the metric:
ρ(r, θ ) = |
r2 + α2 cos2 θ |
|
(3.2.1) |
= r2 + α2 − 2mr + q2 |
(3.2.2) |
||
In terms of these notations the Kerr-Newman metric is given by the following expression for the line-element:
dsKN2 = − |
|
dt − α sin2 θ dt 2 + |
ρ2 |
dr2 |
|
||
ρ2 |
|
|
|||||
|
|
1 |
|
|
|
2 |
|
+ ρ2 dθ 2 + |
|
sin2 θ r2 + α2 − α dt |
|||||
ρ2 |
|||||||
≡ −gμν dxμ dxν = −dτKN2 |
|
(3.2.3) |
|||||
Before studying the properties of such a metric it is useful to emphasize its notable limits in parameter space. They are listed below.
Minkowski If we set all parameters to zero m = α = q = 0 the Kerr-Newman metric (3.2.3) degenerates into the flat Minkowski metric:
dsKN2 → dsMink2 = −dt2 + dr2 + r2 dθ 2 + sin2 dφ2 |
(3.2.4) |
Schwarzschild If we set α = q = 0, but we keep different from zero the mass parameter m = 0 the Kerr-Newman metric (3.2.3) degenerates into the spherical

3.2 The Kerr-Newman Metric |
45 |
symmetric Schwarzschild metric. Indeed, under these assumptions we have:
|
ρ = r; |
ρ2 = 1 |
− 2r |
|
|
|
(3.2.5) |
|||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
so that: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − 1 − |
2m |
2 + 1 − |
2m |
|
−1 |
|||||
dsKN2 |
→ dsSchw2 |
|
dt |
|
|
dr2 |
||||||
r |
r |
|||||||||||
|
|
+ r2 dθ 2 + sin2 dφ2 |
|
|
|
(3.2.6) |
||||||
Reissner-Nordström If we put α = 0 keeping both m and q non-vanishing we obtain the so-called Reissner-Nordström metric which is spherical symmetric but not Ricci-flat. As we shall discuss later on, this metric corresponds to an electrovac solution namely to a solution of the coupled system of Maxwell-Einstein equations. This solution describes the gravitational field generated by an electrically or magnetically charged monopole of mass m and charge q. If α = 0, we have
|
|
|
|
|
|
|
m |
q2 |
|
|
|
|
|
|
ρ = r; |
|
|
= 1 − |
2 |
+ r2 |
|
|
|
|
(3.2.7) |
||||
|
ρ2 |
r |
|
|
|
|||||||||
and |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
|
|
q2 |
|
|
2m |
|
q2 |
|
−1 |
|||
dsKN2 → dsRN2 = − 1 − |
|
+ |
|
dt2 + |
1 − |
|
|
+ |
|
|
dr2 |
|||
r |
r2 |
|
r |
r2 |
||||||||||
+ r2 dθ 2 + sin2 dφ2 |
|
|
|
|
|
|
(3.2.8) |
|||||||
Kerr If we put the charge parameter to zero, namely q = 0, the Kerr-Newman metric degenerates into the Kerr metric which is Ricci-flat but not spherically symmetric. It is only axial-symmetric and it describes a rotating black-hole of mass
m and angular momentum J = mα. In this case we have |
|
|
|
|
|
|||||||
ρ = |
r; |
= |
0 ≡ r2 + α2 − 2mr |
|
|
(3.2.9) |
||||||
and we find: |
|
|
|
|
|
|
|
|
|
|
|
|
dsKN2 → dsKerr2 |
|
0 |
dt − α sin2 θ dt 2 + |
ρ |
2 |
|
dr2 |
|
|
|||
= − |
|
|
|
|
||||||||
ρ2 |
|
0 |
|
|
|
|||||||
|
+ ρ2 dθ 2 |
1 |
sin2 θ r2 + α2 − α dt |
2 |
|
|||||||
|
+ |
|
(3.2.10) |
|||||||||
|
ρ2 |
|||||||||||
3.2.1 Riemann and Ricci Curvatures of the Kerr-Newman Metric
The next step in the analysis of the proposed metric (3.2.3) is the construction of the corresponding curvature forms. As usual we adopt the vielbein formalism and we

46 3 Rotating Black Holes and Thermodynamics
aim at the construction first of the spin connection ωab , secondly of the curvature 2-form Rab , from which we will extract the Riemann and Ricci tensors.
As written in (3.2.3) the Kerr-Newman metric is already presented as a sum of four squares so that singling out the vielbein 1-forms is an immediate task. Indeed
if we define: |
|
|
|
|
|
|
|
|
|
||
V 0 = |
√ |
|
|
dt − α sin2 θ dφ ; |
V 1 = |
|
ρ |
|
|
||
|
|
|
|
|
|||||||
|
|
|
√ |
|
|
dr |
|
||||
ρ |
|
(3.2.11) |
|||||||||
|
|
|
|
||||||||
V 2 = ρ dθ ; |
V 3 = |
|
sin θ |
r2 + α2 dφ − α dt |
|
||||||
|
ρ |
||||||||||
we obtain: |
|
|
|
|
|
|
|
|
|
||
dτKN2 |
≡ −dsKN2 = V a V bηab; |
ηab = diag(+, −, −, −) |
(3.2.12) |
||||||||
Next we consider the construction of the torsionless spin-connection defined by:
dV a + ωab V cηbc = 0
The solution of (3.2.13) is the following one:
ω01 |
= |
(2rq2 − 2mr2 |
+ mα2 + rα2 + (m − r)α2 cos 2θ ) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2√ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Δρ3 |
|
|
|||||||||||
|
|
α2 cos θ sin θ |
|
|
|
|
|
α√ |
|
|
|
cos θ |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ω02 = |
|
|
|
|
|
|
V 0 + |
|
|
|
|
|
|
|
V |
3 |
|
|||||||||
|
|
ρ3 |
|
|
|
|
|
ρ3 |
|
|
||||||||||||||||
ω03 = |
αr sin θ |
1 − |
α√ |
|
|
|
cos θ |
V 2 |
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ρ3 |
|
|
|
|
|
ρ3 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
α2 cos θ sin θ |
|
|
|
|
|
r√ |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ω12 = |
|
|
|
|
|
V 1 + |
|
|
V 2 |
|
|
|||||||||||||||
|
|
ρ3 |
|
|
ρ3 |
|
|
|||||||||||||||||||
ω13 = |
αr sin θ |
0 + |
r√ |
|
V 3 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
V |
|
|
|
|
|
|
|
|||||||||||||||
ρ3 |
|
|
ρ3 |
|
|
|
|
|
||||||||||||||||||
ω23 |
= |
α√ |
|
|
sin θ cot θ V 0 |
+ |
(r2 |
+ α2) cot θ V 3 |
||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
ρ3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ3 |
|
|
|||||
(3.2.13)
V0 + rα sin θ V 3
ρ3
(3.2.14)
Relying on the above result we can proceed to the calculation of the curvature 2- form, defined by:
Rab = dωab + ωac ωdbηcd |
(3.2.15) |
and we obtain the following result:
3.2 The Kerr-Newman Metric |
47 |
|||
R01 = |
1 |
− 4mr3 − 6mα2r + q2 α2 − 6r2 + q2 − 6mr α2 cos 2θ V 0 V 1 |
||
|
||||
2ρ6 |
||||
|
|
− 2α cos θ 4rq2 + m α2 − 6r2 + mα2 cos 2θ V 2 V 3 |
|
|
R02 = |
1 |
α2 − 2r2 q2 + mr 2r2 − 3α2 + q2 − 3mr α2 cos 2θ V 0 V 2 |
||
2ρ6 |
||||
|
|
− α cos θ 4rq2 + m α2 − 6r2 + mα2 cos 2θ V 1 V 3 |
|
|
R03 |
= |
1 |
α2 − 2r2 q2 + mr 2r2 − 3α2 + q2 − 3mr α2 cos 2θ V 0 V 3 |
|
2ρ6 |
||||
|
|
+ α cos θ 4rq2 + m α2 − 6r2 + mα2 cos 2θ V 1 V 2 |
(3.2.16) |
|
R12 |
= |
1 |
α2 − 2r2 q2 + mr 2r2 − 3α2 + q2 − 3mr α2 cos 2θ V 1 V 2 |
|
|
||||
2ρ6 |
||||
|
|
− α cos θ 4rq2 + m α2 − 6r2 + mα2 cos 2θ V 0 V 3 |
|
|
R13 |
= |
1 |
α cos θ 4rq2 + m α2 − 6r2 + mα2 cos 2θ V 0 V 2 |
|
2ρ6 |
|
|||
|
|
+ α2 − 2r2 q2 + mr 2r2 − 3α2 + q2 − 3mr α2 cos 2θ V 1 V 3 |
||
R23 |
= |
1 |
2α cos θ 4rq2 + m α2 − 6r2 + mα2 cos 2θ V 0 V 1 |
|
2ρ6 |
|
|||
+ q2 − 2mr 2r2 − 3α2 − 3α2 cos 2θ V 2 V 3
Inspecting (3.2.16) we see that the intrinsic components of the curvature 2-form, namely the flat index components of the Riemann tensor, are functions only of the coordinates θ and r, while they do not depend on the time t and on the azimuthal angle φ. This is so because the Kerr-Newman metric is static and axial symmetric namely it admits the following two Killing vector fields:
k |
≡ |
∂ |
; |
k |
∂ |
(3.2.17) |
|
∂t |
∂φ |
||||||
|
˜ ≡ |
|
Furthermore we also note that the non-vanishing components of the Riemann tensor are of the form:
Rabcd = (· · · )ab × δcdab + (· · · )ab × εabcd |
(3.2.18) |
Extracting from (3.2.16) the Riemann tensor Rabcd , we can calculate the Ricci tensor defined by:
Ricab ≡ ηamR |
mn |
(3.2.19) |
bn |

48 |
|
|
|
|
|
3 Rotating Black Holes and Thermodynamics |
||||
and we obtain the following result: |
|
|
|
|
|
|
|
|||
|
= |
|
|
|
1 |
0 |
0 |
0 |
|
|
|
2ρ4 |
0 |
0 |
1 |
0 |
|
||||
Ricab |
|
|
q2 |
|
0 |
−1 |
0 |
0 |
|
(3.2.20) |
|
|
|
|
0 |
0 |
1 |
|
|||
|
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
We wonder which kind of matter can produce a stress-energy tensor of the form (3.2.20) so that the constructed metric might be an exact solution of Einstein field equations. The answer is very simple: an electromagnetic field!
Let us consider the general form of the stress energy tensor for a Maxwell field. From the Maxwell action:
AMaxwell = − 1 d4x −detgFμρ Fνσ gμν gρσ
4
varying with respect to the metric we obtain: |
|
|
|
||
Tμν(Maxw) = − |
1 |
Fμρ Fνσ gρσ + |
1 |
gμν |F |2 |
|
|
|
|
|||
2 |
8 |
||||
where we defined:
(3.2.21)
(3.2.22)
|F |2 ≡ Fμρ Fνσ gμν gρσ = FacFbd ηabηcd |
(3.2.23) |
The stress-energy tensor Tμν(Maxw) is traceless (gμν Tμν(Maxw) = 0) and in flat indices takes the same form as in curved indices:
Tab(Maxw) = − |
1 |
FacFbd ηcd + |
1 |
ηab|F |2 |
(3.2.24) |
|
|
|
|
||||
2 |
8 |
|||||
For the particular case of an electromagnetic field of the form:
|
|
F01 |
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
0 |
F01 |
|
0 |
|
|
0 |
|
|
|
Fab |
= −0 |
0 |
|
|
0 |
|
|
F23 |
|
|
||
|
|
0 |
0 |
− |
F |
23 |
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
||||
Equation (3.2.24) yields the result: |
|
|
|
|
|
|
|
|
|
|||
T (Maxw) |
1 |
F 2 |
F 2 |
0 |
−1 |
0 |
0 |
|||||
|
|
|
|
|
|
1 |
0 |
|
0 |
0 |
|
|
ab |
= |
|
01 + 23 |
|
0 |
0 |
1 0 |
|
||||
4 |
||||||||||||
|
|
|
|
|
|
0 |
0 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.2.25)
(3.2.26)
Due to tracelessness of the stress-energy tensor, Einstein field equations reduce to:
Ricab = κTab(Maxw) |
(3.2.27) |
