4.6 The New Scenario of the Inflationary Universe

Fig. 4.21 Alan Guth, Andrei Linde and Paul J. Steinhardt, the fathers of the Inflationary Universe scenario

to the creation of the Inflationary Universe paradigm (see Fig. 4.21). Alan Guth, born in the USA in 1947 is professor at the Massachussetts Institute of Technology, Paul J. Steinhardt, also born in the US, is Einstein professor of Physics at Princeton University, while Andrei Linde, born in Moscow, studied and worked there, becoming one of the most famous and distinguished cosmologists of the world. In the mid nineties of the XXth century he accepted the invitation of Stanford University to join the faculty of its Physics Department.

There are many formulations of the inflationary theory and its details crucially depend on the structure of the unified theory of all interactions that will prove to be the one chosen by Nature. For instance, within the framework of supergravity, regarded as the low-energy limit of superstring theory, there are several interesting

possibilities to implement the inflationary scenario and determine its parameters in agreement with the experimental data that are piling up. However, beyond its detailed structure, the great value of the Inflationary Universe is that it provides a very simple conceptual paradigm, up to now without any rivals, capable of explaining the isotropy, homogeneity and spatial flatness of the Universe.

Here we do not dwell too much on explanations of Inflation, which will be discussed in a detailed mathematical way in later sections. We just mention that the generic mechanism, capable of preparing homogeneous, isotropic and spatially flat boundary conditions, consists of a primeval phase of exponential expansion that should have taken place before the age of decoupling and should have also gracefully ended. On its turn, an exponential expansion takes place when gravity becomes repulsive and this happens when the energy content of the Universe is mainly provided by vacuum energy, for instance the potential energy V (ϕ) of one or more scalar fields ϕ. Hence, the inflationary universe scenario is just a generic property of any fundamental theory of particle interactions that contains scalar fields. Fundamental spin zero fields, namely scalars, have not yet been detected, but their presence is ubiquitous in all approaches to unification, they are essential in all versions of supergravity theory and they are necessary because of symmetry breaking. From this point of view we can say that Cosmology provides another indirect evidence for the existence of this type of particles whose detection is by now overdue.4

4.7The End of the Second Millennium and the Dawn of the Third Bring Great News in Cosmology

The end of the XXth century and the beginning of the XXIst brought new developments into Cosmology, almost of the same relevance as the discovery of the Hubble law in 1929. A new series of data which have become available starting from 1998 caused a substantial revolution in the subject that, by now, has entered an entirely new phase. Before 1998, theoretical Cosmology was mostly a matter of conjectures and speculations with a remote chance of verification or disproval. At the end of the next decade, in mid 2009, when the European Satellite Planck was launched from the French basis in Guyana towards the Lagrangian point L2 (see Fig. 4.25), theoretical cosmology had already evolved into a science that deals with the explanation of a series of facts established in a substantially firm way. Let us list these facts:

1.Our Universe is spatially flat.

2.Our Universe is presently in a phase of accelerating expansion.5

4July 4th 2012 it was officially announced by CERN that both ATLAS and CMS detectors had discovered a new bosonic particle that seems to be the long sought for spin zero particle implementing the Higgs symmetry breaking mechanism.

5The 2011 Nobel Prize in Physics was awarded to Saul Perlmutter of the Lawrence Berkeley National Laboratory, Brian Schmidt of the Australian National Laboratory and to Adam Reiss of the Johns Hopkins University, for their 1998 discovery of the present accelerated expansion of the Universe (see Fig. 4.22).

found. Indeed the spectra and the intrinsic luminosity of all known, nearby, type IA supernovae had been revealed to be equal. A fascinating theoretical explanation of these standard candles was also guessed. It was conjectured that type IA supernovae explosions originate from the following phenomenon. In a binary stellar system one of the two companions reaches the end of its life transforming first into a red-giant and then into a white dwarf, sustained against gravitational collapse by the degeneracy pressure of the electron gas, as we explained in Chap. 6 of Volume 1. The other star is still alive and active. If conditions of proximity and relative mass are right, there will be a steady stream of material from the active star slowly accreting onto the white dwarf. Over the millions of years, the dwarf’s mass increases steadily until it reaches the Chandrasekhar limit explained in Chap. 6 of Volume 1. At that point a runaway thermonuclear explosion is triggered which destroys the dwarf and manifests itself in observations as a type IA supernova. The crucial point is that the Chandrasekhar mass, whose value 1.4M is determined in terms of fundamental constants of Nature, is the same for any supernova IA. This fixes the intrinsic luminosity of the event in an absolute way giving rise to an ideal standard candle which is luminous enough to be seen also in very distant galaxies. Indeed at the time of explosion and typically for a week after that, a supernova is as luminous as an entire galaxy.

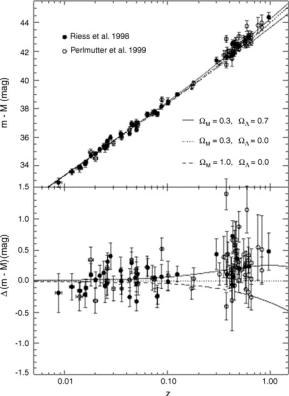
Using systematically these standard candles and surveying the sky at very high redshifts z, namely at very large distances from our observation point in the Milky Way, by the end of 1998, the two collaborations groups were ready to present their Hubble plots of the redshift versus distance which, for the first time in history, showed their deviation from linearity (see Fig. 4.23). In this way, we got the first estimate of the deceleration parameter which is defined as follows:

and parameterizes the aforementioned deviations. To see that, it suffices to consider the Taylor expansion of the scale factor around the present time:

and recall the definition (4.3.3) of the redshift factor which can be rewritten as follows:

since, as we already mentioned and as we will prove later on, the ratio between the wave-length of a photon at the present time t0 and at the time of emission t is the same as the ratio of the scale factors at the same instants of time: λ(t0)/λ(t) = a(t0)/a(t). Inserting the Taylor expansion (4.7.2) into (4.7.3) and inverting the relation we find:

Fig. 4.23 Using type IA supernovae as standard candles and systematically detecting them in very remote galaxies has provided the means to determine the deviation of the Hubble law from linearity at high redshifts, in other words to estimate the acceleration of the Universe expansion which has proved to be positive. This is consistent with the existence of dark energy, alias of a positive cosmological constant

where c is the speed of light and the distance between us and the source as been approximated as d c(t − t0). Equation (4.7.4) presents the form of the first quadratic correction to the linear Hubble law which was experimentally evaluated for the first time in history in 1998. The surprise was immense since the deceleration parameter q0 turned out to be negative, in other words it was revealed that our Universe is actually accelerating its expansion at the present time, since a(t¨ 0) > 0.

In later sections, studying Friedman equations, we will show that the acceleration parameter can be positive only if the energy content of the Universe is dominated by vacuum energy rather than by ordinary matter and radiation. The evaluation of q0 was therefore a direct evaluation of the percentage of vacuum energy filling our Universe: approximately the 70 percent, as it turned out by taking into account the other important results about the CMB anisotropies which became available in the following years.

The satellite WMAP (Wilkinson Microwave Anisotropy Probe) was launched in June 2001 from Cape Kennedy and reached the Lagrangian point L2 wherefrom, during seven years it collected and streamed to Earth very important data on the space distribution of the Cosmic Microwave Background Radiation, in particular measuring its temperature in each direction of the sky. The oscillations of the temperature with respect to its average value T = 2.725 K are of the order of

Fig. 4.24 The microwave image of the primeval sky obtained by the seven year mission WMAP, that has measured the temperature anisotropies of the Cosmic Background Radiation. With variations of the order of few milliKelvin the microwave sky displays hotter and colder spots. As shown in later sections, the temperature variations are a direct measure of the variations in the gravitational potential at the time of decoupling, 400.000 years after the Big Bang and approximately 13 billions of years ago

the milliKelvin; when such hotter and colder spots are reported on a two-sphere representing the sky one obtains an image of the same type as shown in Fig. 4.24.

Such a plot can be regarded as an image of the Last Scattering Surface at the time of decoupling of radiation. Furthermore, because of an effect named Sachs- Wolffe-effect, which we will mathematically explain in later sections, measuring

the temperature variation function δT (x) is nothing else but measuring the primeval

T

gravitational potential Φ(x) that encodes the perturbation of the metric around its homogeneous and isotropic form.

In this way the WMAP mission, which was extremely successful, provided us with a direct measure of the cosmic primeval perturbations just before the time of radiation decoupling and established a new vision of the early Universe.

From the analysis of the CMB spectrum we learnt that our Universe is spatially flat κ = 0 and we could confirm its acceleration, obtaining a more precise evaluation of the amount of vacuum energy (around 72 %).

Furthermore the multipole analysis of the correlation function:

01

confirmed the generic predictions of the Inflationary Universe scenario showing that, with high probability, the physical mechanism which explains the mysterious homogeneity and isotropy of our Universe, alias the Cosmological Principle, is indeed the one for which the 2003 Dirac Medal was awarded. In 2009 a new radio-telescope was launched by the European Space Agency, named Planck (see Fig. 4.25). It also was placed in the Lagrangian point L2 from which it started collecting data on the CMB anisotropies with still higher precision than its predecessor