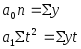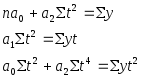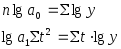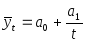- •Тема 1. Статистическое наблюдение Методические указания
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 2. Сводка и группировка данных Методические указания
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 3. Графический метод Методические указания
- •Беларусь
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 4. Статистические показатели
- •10. Что характеризует относительная величина интенсивности?
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 5. Анализ рядов распределения. СтаТиСтическая проверка гипотез Методические указания
- •Решение
- •Распределение студентов по успеваемости
- •Решение
- •Решение
- •Кумулятивные показатели распределения семей по среднедушевому доходу
- •Вспомогательная таблица для расчета теоретических частот нормального распределения
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 6. Выборочное наблюдение Методические указания
- •Формулы необходимого объема выборки для различных способов формирования выборочной совокупности выводятся из соответствующих соотношений, используются при расчете предельных ошибок выборки.
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 7. Анализ интенсивности динамики Методические указания
- •Формулы показателей анализа ряда динамики
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 8. Анализ тенденций развития Методические указания
- •Уравнения, используемые при аналитическом выравнивании динамических рядов
- •Вспомогательные расчеты для определения параметров а0 и а1 уравнения прямой и критерия статистической точности аналитического уравнения
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 9. Индексы Методические указания
- •1. Какой из приведенных символов не связан функциональной зависимостью количественного, качественного и объемного показателей?
- •5. Какая из приведенных формул является индивидуальным индексом себестоимости ?
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Тема 10. Статистические методы изучения
- •ВзаимОсвязей социально-экономических
- •Явлений
- •Методические указания
- •Шкала Чеддока
- •На основе данных аналитической группировки строится график эмпирической линии связи, вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о ее форме.
- •Системы нормальных уравнений для разных форм связи
- •3) Рассчитывается коэффициент ранговой корреляции Спирмена ():;
- •Решение
- •Решение
- •Решение
- •Вспомогательная таблица для расчета параметров уравнения связи
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Ответы на тестовые задания
- •Тема 10
Тема 8. Анализ тенденций развития Методические указания
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития.
Основными показателями, дающими представление о тенденции (тренде) развития явления во времени, являются цепные абсолютные приросты, цепные темпы роста и средние уровни.
Если расчет цепных показателей не позволил выявить тенденцию в ряду динамики, то переходят к обработке ряда с помощью методов, основанных на расчете средних уровней. К таким методам относятся: укрупнение интервалов времени, эмпирическое сглаживание (метод скользящей средней) и аналитическое выравнивание.
Укрупнение интервалов времени. Суть метода укрупнения интервалов времени в динамических рядах состоит в том, что берут данные за промежутки времени большей длительности по сравнению с первоначальными. Например, суточные данные заменяют пятидневными, декадными, месячными; месячные – квартальными, годовыми; годовые – трех-, четырех-, пятилетними и т.д. Укрупнение интервалов следует начинать с наименьшего возможного, т.е. интервала, объединяющего два уровня. В случае, если укрупнение по два уровня не дает возможности увидеть тенденцию, переходят к следующему возможному интервалу.
Сущность метода скользящей средней заключается в замене абсолютных уровней средними арифметическими за определенные периоды. При этом расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
Наиболее
эффективным способом выявления основной
тенденции развития является аналитическое
выравнивание.
При этом уровни ряда динамики выражаются
в виде функции времени: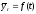 .
Аналитическое выравнивание может быть
осуществлено по любому рациональному
уравнению тренда. Выбор формы уравнения
производится на основе анализа характера
закономерностей динамики изучаемого
явления. В таблице 8.1 приведены системы
уравнений, которые необходимо решить
для определения параметров уравнений,
описывающих тенденции в рядах динамики.
.
Аналитическое выравнивание может быть
осуществлено по любому рациональному
уравнению тренда. Выбор формы уравнения
производится на основе анализа характера
закономерностей динамики изучаемого
явления. В таблице 8.1 приведены системы
уравнений, которые необходимо решить
для определения параметров уравнений,
описывающих тенденции в рядах динамики.
Таблица 8.1
Уравнения, используемые при аналитическом выравнивании динамических рядов
|
Вид уравнения |
Системы уравнений | |
|
Обычный способ рас- чета параметров |
Упрощенный способ расчета параметров | |
|
Прямая:
|
|
|
|
Парабола второго порядка:
|
|
|
|
Показательная
кри-вая: |
|
|
|
Гипербола:
|
|
|
При
анализе рядов динамики в ряде случаев
возникает необходимость в выявлении
сезонных
колебаний.
Для определения сезонных колебаний
обычно анализируются месячные и
квартальные уровни ряда динамики за
год или за несколько лет (в основном не
менее 3-х лет). При выявлении и оценке
сезонности рассчитывают специальные
показатели – индексы сезонности (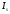 ).
Способы определения индексов сезонности
различны и зависят от характера ряда
динамики.
).
Способы определения индексов сезонности
различны и зависят от характера ряда
динамики.
В
рядах, не имеющих ярко выраженной
тенденции развития (или она не наблюдается
совсем), изучение сезонности основано
на методе
простой средней. Сущность
этого метода заключается в том, что
показатели сезонной волны определяются
процентным отношением соответствующих
средних месячных (квартальных уровней)
к их общей средней за весь изучаемый
период. Следовательно, при изучении
помесячной сезонности сначала средние
по месяцам и среднюю годовую исчисляют
из данных за несколько лет (по простой
арифметической), а затем эти средние по
месяцам года (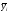 )относят
к средней годовой (к среднему месячному
уровню для взятых лет) (
)относят
к средней годовой (к среднему месячному
уровню для взятых лет) (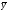 ),
т.е. индекс сезонности исчисляется по
формуле:
),
т.е. индекс сезонности исчисляется по
формуле:
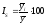
В
рядах динамики, имеющих тенденцию
развития, для определе-ния индексов
сезонности вначале рассчитывают уровни,
сглаженные методом скользящей средней
или выравненные по определенной функции.
Индексы сезонности вычисляются отношением
фактического уровня за определенный
квартал или месяц (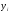 )
к выравненному за этот же период (
)
к выравненному за этот же период ( ).
В результате при использовании, например,
квар-тальных данных за три года получают
двенадцать индексов сезонности:
).
В результате при использовании, например,
квар-тальных данных за три года получают
двенадцать индексов сезонности:
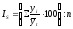 .
.
Затем исчисляют средние индексы сезонности для одноименных кварталов за рассматриваемые годы:
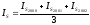 .
.
В качестве аналитической формы сезонной волны иногда применяется уравнение следующего вида:
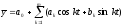 ,
,
где
k
-
порядок гармоники тригонометрического
многочлена; t
- время;
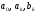 -
параметры ряда Фурье.
-
параметры ряда Фурье.
Это уравнение представляет собой ряд Фурье, где время (t) выражается в радиальной мере или в градусах:
|
Месяцы t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Радиальная мера |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Градусы |
0 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
330 |
|
Уровни, уi |
у1 |
у2 |
у3 |
у4 |
у5 |
у6 |
у7 |
у8 |
у9 |
у10 |
у11 |
у12 |
Обычно при выравнивании по ряду Фурье рассчитывают не более четырех гармоник и затем уже определяют, с каким числом гармоник наилучшим образом отражается периодичность изменения уровней ряда.
Например, при k = 1 уравнение ряда Фурье будет иметь вид:
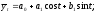
при
k
=
2 соответственно:
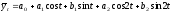 .
.
Параметры уравнения находят по способу наименьших квадратов. При этом формулы, используемые для исчисления указанных выше параметров уравнения ряда Фурье имеют вид:
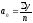 ;
;
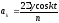 ;
;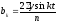 .
.
Тесты
В чем суть приема “укрупнение периодов времени”?
1) определяются средние уровни с помощью математического урав-нения; 2) отыскиваются и сравниваются базисные темпы роста; 3) производится замена абсолютных данных средними арифметическими при постепенном исключении из рассмотрения первых уровней и включении последующих уровней; 4) производится замена абсолютных уровней данными.
2. Каким методом целесообразно сглаживать короткие динамические ряды?
1) с помощью скользящей средней; 2) путем укрупнения интервалов; 3) с помощью аналитического выравнивания; 4) исчислением средних по укрупненным интервалам.
3. Что является первым этапом аналитического выравнивания динамического ряда?
1) выявление характера динамики явления; 2) расчет выровненных уровней; 3) определение параметров уравнения по способу наименьших квадратов; 4) выбор математического выражения закономерности.
4.
В каком случае упрощается система
уравнений для нахождения параметров
уравнения
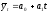 ?
?
1) принимается четное количествоо периодов; 2) принимается нечетное количество периодов; 3) начало отсчета времени переносится в середину рассматриваемого периода; 4) расчет выполняется табличным методом.
5.
По какой формуле можно определить
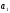 ?
?
1)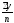 ;
2);
;
2);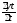 ;
3)
;
3)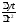 4)
4)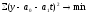 .
.
6. В чем суть приема эмпирического сглаживания?
1) определяются средние уровни с помощью математического урав-нения; 2) отыскиваются и сравниваются базисные темпы роста; 3) про-изводится замена абсолютных данных средними арифметическими при постепенном исключении из рассмотрения первых уровней и включении последующих уровней; 4) производится замена абсолютных данных средними арифметическими за укрупненные периоды.
7. В чем суть метода наименьших квадратов?
1)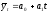 ;
2)
;
2)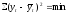 ;
3)
;
3)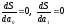 ;
4)
;
4)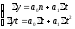 .
.
8.
Какой расчет необходимо сделать для
определения параметров уравнения
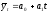 ?
?
1)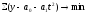 ;
2)
;
2)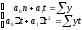 ;
3)
;
3) .
.
9.
Какую систему уравнений надо решить
для определения параметров уравнения
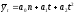 ?
?
1)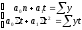 ;2)
;2)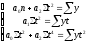 ;3)
;3)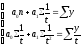 ;4)
;4)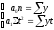
Решение типовых задач
Пример 1. Имеются следующие данные о товарных запасах торгового дома за 1994 – 2002гг., млн. грн.
1994 г. 1995 г. 1996 г. 1997 г. 1998 г. 1999 г. 2000 г. 2001 г. 2002 г.
10,0 10,7 12,0 10,3 12,9 16,3 15,6 17,8 18,0
Требуется выявить основную тенденцию изменения товарных запасов, используя следующие методы: 1) укрупнение интервалов времени; 2) эмпирическое сглаживание; 3) аналитическое выравнивание по прямой.
Решение
1. Укрупнение интервалов времени. Произведем укрупнение интервалов, начиная с объединения двух уровней:
1994-1995гг.:10,0+10,7=20,7 млн.грн; 1998-1999гг.:12,9+16,3=29,2 млн.грн
1996-1997гг.:12,0+10,3=22,3 млн.грн; 2000-2001гг.:15,6+17,8=33,4млн.грн.
По результатам проведенных расчетов проявляется тенденция роста изучаемого показателя. Используя полученные суммы по периодам, можно рассчитать ступенчатые средние. Для наглядности итоги расчетов оформим в таблице.
Таблица 8.2
Укрупнение интервалов времени и ступенчатые средние, исчисленные по данным о товарных запасах торгового дома за 1994 – 2002 гг.
|
Интервалы времени |
Суммы по периодам,млн.грн. |
Ступенчатые средние,млн.грн. |
|
1994 – 1995 |
20,7 |
10,4 |
|
1996 – 1997 |
22,3 |
11,2 |
|
1998 – 1999 |
29,2 |
14,6 |
|
2000 – 2001 |
33,4 |
17,7 |
|
2002 |
- |
18,0 |
Ступенчатые средние наглядно отображают тенденцию роста товарных запасов торгового дома за 1994–2002гг.
2. Эмпирическое сглаживание. Сгладим данный ряд динамики по трехлетней скользящей средней, т.к. период колебаний запасов равен трем годам. Исчислим:
средний
уровень за 1994-1996гг.: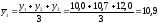 млн.грн.;
млн.грн.;
средний
уровень за 1995-1997гг.: млн.грн.;
млн.грн.;
средний
уровень за 1996-1998гг.: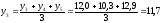 млн.грн.
млн.грн.
и т.д. Результаты расчета трехлетней суммы и скользящей средней по периодам представим в таблице (табл. 8.3).
Таблица 8.3
Сглаживание динамического ряда товарных запасов за 1994 – 2002гг. с помощью трехлетней скользящей средней
|
Годы |
Товарные за-пасы,млн.грн. |
Период сглаживания |
Середин-ный год |
3х-летние сум-мы,млн.грн |
3х-летние скользящие средние,млн. грн |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1994 |
10,0 |
– |
– |
– |
– |
|
1995 |
10,7 |
1994 - 1996 |
1995 |
32,7 |
10,9 |
|
1996 |
12,0 |
1995 - 1997 |
1996 |
33,0 |
11,0 |
|
1997 |
10,3 |
1996 - 1998 |
1997 |
35,2 |
11,7 |
|
1998 |
12,9 |
1997 - 1999 |
1998 |
39,5 |
13,2 |
|
1999 |
16,3 |
1998 - 2000 |
1999 |
44,8 |
14,9 |
|
2000 |
15,6 |
1999 - 2001 |
2000 |
19,7 |
16,6 |
|
2001 |
17,8 |
2000 - 2002 |
2001 |
51,4 |
17,1 |
|
2002 |
18,0 |
– |
– |
– |
– |
Таким образом, нами получен новый ряд динамики (гр. 4 и 6), в котором наблюдается тенденция роста запасов за исследуемый период времени.
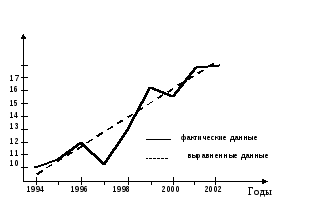
3. Аналитическое выравнивание. При выборе функции, описывающей тенденцию, логический анализ динамического ряда должен опираться на графические изображение его. Нанесем на график приведенные данные. Ломаная кривая, отображающая фактические данные, позволяет выбрать в качестве функции, описывающей тренд, уравнение прямой (рис.8.1).
Уравнение
прямой выражается формулой:
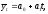
где
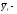 значение
выравненного ряда (теоретические
уровни);
значение
выравненного ряда (теоретические
уровни);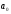 и
и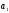 -
параметры уравнения прямой;
-
параметры уравнения прямой; показатель
времени.
показатель
времени.
Товарные запа-сы, млн. грн.
18
Рис. 8.1. Товарные запасы торгового дома за 1994–2002гг.
Для
нахождения параметров
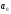 и
и необходимо решить систему нормальных
уравнений:
необходимо решить систему нормальных
уравнений: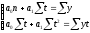
где у – фактические уровни ряда динамики; п – количество уровней.
Для упрощения расчетов в рядах динамики обозначают время так, чтобы начало отсчета времени приходилось на середину рассматриваемого периода. Если количество уровней четное, то условное обозначение показателя времени принимает вид:
Годы 1997 1998 1999 2000 2001 2002
t -5 -3 -1 +1 +3 +5
Если количество уровней нечетное, условное обозначение t имеет вид:
Годы 1996 1997 1998 1999 2000 2001 2002
t -3 -2 -1 0 1 2 3
Таблица 8.4