2.1.2. Законы распределения случайных величин, используемые в теории надежности

Использовать надежностные характеристики объекта, заданные в виде таблицы, весьма неудобно. Поэтому по результатам эксперимента подбирают аналитическую формулу, которая наиболее удачно подходит в данном случае, и определяют коэффициенты этой формулы. Наиболее ти­пичные формулы называются законами распределения случайных вели­чин. Рассмотрим наиболее распространенные законы.

Показательное (экспоненциальное) распределение

Показательное распределение характерно тем, что интенсивность по­стоянна ( = const). Отсюда

. (2.16)

П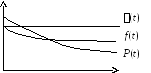римерный вид соответствующих кривых показан на рис. 2.2.

Рис. 2.2. Примерный вид основных показателей

надежности при экспоненциальном распределении

Показательное распределение применяется на практике очень ши­роко. При этом отказы элементов рассматриваются как пуассоновский по­ток отказов, обладающий следующими свойствами: простейший (время между отказами распределено по экспоненциальному закону), ординарный (два события не могу произойти в один и тот же момент времени), стацио­нарный без последействий.

Некоторые данные об интенсивности отказов компонентов вычисли­тельных систем приведены в приложении.

Пример 2.2. Пусть в результате испытаний получены следующие значения:

ti	0	2	4	6	8	10	12	14	16	18	20
N(ti)	1000	905	818	741	670	606	549	497	449	407	368

Проведя расчеты _i, видим, что _i  0,05 и не зависит от t_i. Следова­тельно, можно сделать вывод, что закон распределения надежности дан­ного объекта является экспоненциальным, при этом  = 0,05. Тогда Т = = 1/ = 20 ч. Найдем Р(t) и Q(t) за 30 ч согласно (2.16):

Р(30) = е^–0,0530 = 0,223,

Q(30) = 1 – P(30) = 0,777

и за 100 ч:

Р(100) = е^–5 = 0,067,

Q(100) = 1 – P(100) = 0,9933.

В теории надежности существует правило: считается, что распреде­ление экспоненциальное, если результаты эксперимента явно этому не противоречат.

Усеченное нормальное распределение

При нормальном (гауссовом) распределении случайной величины ось абсцисс имеет протяженность от – до +. Поскольку время t не мо­жет быть отрицательной величиной, в теории надежности используется усеченное нормальное распределение.

Усеченным нормальным распределением случайной величины назы­вается распределение, получаемое из нормального при ограничении интер­вала возможных значений этой величины.

Основными параметрами для нормального распределения являются: Т – среднее значение наработки на отказ, _t – среднеквадратическое откло­нение:

(2.17)

где Ф(и) – нормированная функция нормального распределе­ния. Значения Ф(и) приведены в литературе. При этом Ф(–и) = 1 – Ф(и),

. (2.18)

Значения (и) приведены в литературе. При этом (–и) = (и),

(2.19)

Примерный вид соответствующих кривых представлен на рис. 2.3.

Нормальное распределение может использоваться при исследовании надежности объектов, отказы которых обусловлены действием какого-то одного доминирующего фактора.

Пример 2.3. Пусть параметры нормального распределения Т = 100 ч, = 1000 ч². Найти Р(70), Q(70), (70), P(130), Q(130), (130). Из формул (2.17)–(2.19):

Р(70) = 1 – Ф= 1 – Ф(–0,95) = Ф(0,95) = 0,829,

Q(70) = 1 – Р(70) = 0,171,

 (70) = = 0,306,

Р(130) = 1 – Ф= 1 – Ф(0,95) = 0,171,

Q(130) = 1 – Р(130) = 0,829,

(130) = = 1,485.