Вариант №29
На складе имеются 15 кинескопов, из них 10 изготовлены Львовским заводом. Найти вероятность того, что среди 5 взятых наудачу кинескопов окажутся 3 кинескопа Львовского завода.
Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0.7, для второго – 0.8, для третьего – 0.9. Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков; хотя бы один стрелок.
Вероятности безотказной работы каждого из элементов электрической цепи, пока-
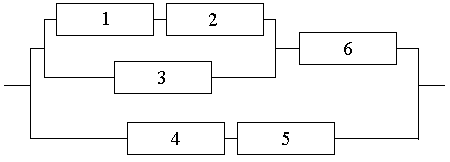
занной на рисунке, равны соответственно: p1 = p2 = 0.95; p3 = p4 = p5 = 0.9; p6 = 0.85. Найти вероятность отказа цепи.
В двух урнах находится шары: в первой 14 красных и 6 зеленых; во второй 15 красных и 8 зеленых. Из первой урны последовательно один за другим вынуты 2 шара и переложены во вторую. Затем из второй урны извлекаются наудачу один шар. Какова вероятность того, что шар зеленый?
На участке 8 станков. Вероятность отказа каждого из них 0.1. Найти вероятность того, что в данный момент работает не менее половины станков.
Произведено 1200 независимых выстрелов по цели. Вероятность попадания при одном выстреле равна 0.85. Найти вероятность того, что будет не более 150-ти промахов в цель; ровно 150 промахов в цель.
Устройство состоит из 400 независимо работающих однотипных элементов. Вероятность надежной работы каждого в течение времени t равна 0.995. Найти вероятность того, что по истечении этого времени работают не менее трех элементов.
Устройство состоит из 5 независимо работающих элементов. Вероятность надежной (безотказной) работы каждого элемента в одном испытании равна 0.9. Составить закон распределения случайной величины X – числа отказавших элементов при одном испытании. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.
Случайная величина X задана плотностью вероятностей:
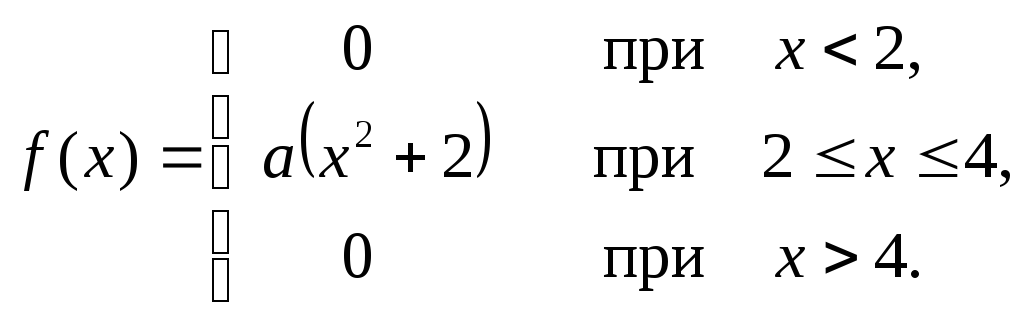
Найти коэффициент a, функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность попадания X в интервал (0.2, 0.8). Построить графики плотности и функции распределения и на показать них математическое ожидание и среднее квадратическое отклонение.
На станке изготавливается деталь. Ее длина X – случайная величина, распределенная по нормальному закону с параметрами: a = 500 см, σ = 1 см. Найти вероятность того, что длина детали заключена между 498 см и 501 см. Какое отклонение длины детали от a можно гарантировать с вероятностью 0.9; 0.99? В каких пределах будут лежать практически все размеры деталей?
На основе данных о результатах определения уровня депрессивности поведения (уровня тревожности поведения, страха, ощущения неотвратимости катастрофы, шкала №2) у 47-ми подростков сформировать таблицу значений относительных час-
-
№
Д [%]
№
Д [%]
№
Д [%]
№
Д [%]
№
Д [%]
1
3.0
11
8.1
21
9.6
31
10.6
41
12.1
2
4.1
12
8.3
22
9.7
32
10.7
42
12.2
3
5.5
13
8.5
23
9.8
33
10.8
43
12.4
4
6.0
14
8.7
24
9.9
34
10.9
44
12.6
5
6.4
15
8.9
25
10.0
35
10.9
45
12.8
6
7.1
16
9.1
26
10.1
36
11.1
46
13.4
7
7.3
17
9.2
27
10.2
37
11.3
47
14.2
8
7.5
18
9.3
28
10.3
38
11.5
9
7.7
19
9.4
29
10.4
39
11.6
10
7.9
20
9.5
30
10.5
40
11.9
тот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
3.0
68.1
11
8.1
56.0
21
9.6
51.7
31
10.6
47.8
41
12.1
39.5
2
4.1
66.0
12
8.3
55.5
22
9.7
51.4
32
10.7
46.8
42
12.2
38.4
3
5.5
64.53
13
8.5
55.1
23
9.8
51.0
33
10.8
46.3
43
12.4
37.0
4
6.0
63.43
14
8.7
54.6
24
9.9
50.6
34
10.9
45.5
44
12.6
35.3
5
6.4
62.0
15
8.9
54.1
25
10.0
50.2
35
10.9
44.8
45
12.8
33.5
6
7.1
61.2
16
9.1
53.4
26
10.1
49.8
36
11.1
44.3
46
13.4
31.4
7
7.3
59.5
17
9.2
53.2
27
10.2
49.4
37
11.3
43.7
47
14.2
29.8
8
7.5
58.5
18
9.3
52.3
28
10.3
49.0
38
11.5
43.2
9
7.7
57.3
19
9.4
52.1
29
10.4
48.6
39
11.6
42.1
10
7.9
56.6
20
9.5
51.9
30
10.5
48.2
40
11.9
41.0
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 7 и 6 равных частичных интервалов соответственно.