Вариант №10
Бригада рабочих, состоящая из 6 сборщиков и 10 разнорабочих, произвольным образом делится на две равные группы. Какова вероятность того, что в каждой группе окажется одинаковое число сборщиков?
В урне 7 черных и 5 желтых шаров. Найти вероятность того, что среди наудачу извлеченных 4 шаров окажется более 2-х желтых.
Вероятность работы каждого элемента p = 0.9. Определить, какая из двух функциональных цепей надежнее.
Три станка-автомата штампуют однотипные детали. Первый станок вырабатывает 45% всех деталей, второй – 35%, третий – 20%. При этом каждый из станков штампует нестандартных деталей в среднем соответственно 2.5%; 2%; 1.5%. Найти вероятность того, что наудачу взятая со склада деталь стандартна.
На автобазе имеется 12 автомашин. Вероятность выхода на линию каждой машины равна 0.8. Найти вероятность нормальной работы автобазы в ближайший день, если для этого необходимо иметь на линии не менее 9 автомашин.
Пусть вероятность того, что наудачу взятая деталь нестандартна, равна 0.1. Найти вероятность того, что среди пятисот взятых наудачу деталей окажется не более шестидесяти нестандартных; ровно шестдесят нестандартных.
При штамповке металлических клемм получается в среднем 99% годных. Найти вероятность того, что среди 500 клемм будет хотя бы одна бракованная; не более двух бракованных.
Вероятность попадания в цель при одном выстреле из орудия равна 0.4. Производится 4 выстрела. Составить закон распределения дискретной случайной величины X – числа попаданий. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.
Дифференциальная функция распределения вероятностей случайной величины X равна:
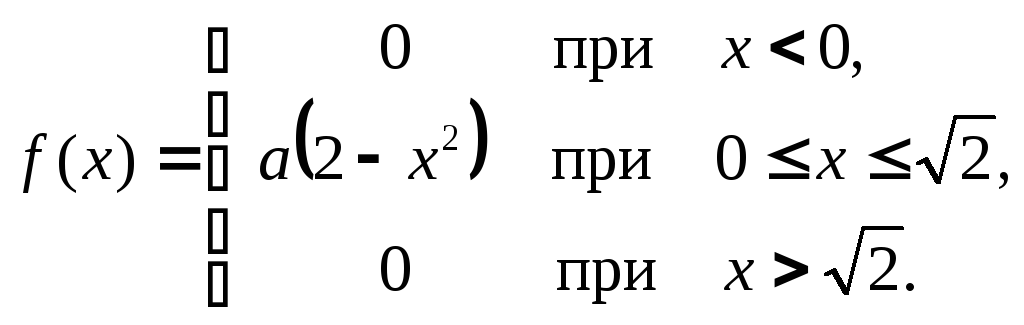
Найти коэффициент a, интегральную функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность P(0<X<1). Построить графики плотности и функции распределения и на показать них математическое ожидание и среднее квадратическое отклонение σ(X).
Диаметр детали – случайная величина, распределенная по нормальному закону с параметрами: a = 60 мм, σ = 0.09 мм. Найти вероятность того, что диаметр наудачу взятой из партии детали составит от 59.8 мм до 60.2 мм; отличается от a не более, чем на 0.06 мм? Какое отклонение диаметра детали от a можно гарантировать с вероятностью 0.95? В каком интервале с вероятностью 0.9973 будут заключены диаметры практически всех изготовленных деталей?
На основе данных о результатах 48-ми измерений времени 30%-ой аккомодации глаза лисицы в условиях абсолютной темноты сформировать таблицу значений относи-
-
№
ta [мин]
№
ta [мин]
№
ta [мин]
№
ta [мин]
№
ta [мин]
1
3.0
11
10.3
21
12.8
31
15.3
41
18.6
2
4.0
12
10.7
22
13.0
32
15.5
42
19.0
3
5.0
13
11.0
23
13.2
33
15.7
43
19.6
4
6.0
14
11.2
24
13.4
34
15.9
44
20.2
5
6.9
15
11.4
25
13.6
35
16.2
45
20.8
6
7.6
16
11.6
26
13.8
36
16.6
46
21.6
7
8.2
17
11.9
27
14.0
37
16.9
47
23.0
8
8.8
18
12.2
28
14.4
38
17.4
48
24.0
9
9.3
19
12.4
29
14.8
39
17.8
10
9.8
20
12.6
30
15.1
40
18.2
тельных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 8 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
3.0
91
11
10.3
100
21
12.8
102
31
15.3
104
41
18.6
108
2
4.0
93
12
10.7
100
22
13.0
102
32
15.5
104
42
19.0
109
3
5.0
95
13
11.0
101
23
13.2
103
33
15.7
105
43
19.6
109
4
6.0
96
14
11.2
101
24
13.4
103
34
15.9
105
44
20.2
110
5
6.9
97
15
11.4
101
25
13.6
103
35
16.2
106
45
20.8
111
6
7.6
97
16
11.6
101
26
13.8
103
36
16.6
106
46
21.6
112
7
8.2
97
17
11.9
101
27
14.0
103
37
16.9
106
47
23.0
113
8
8.8
97
18
12.2
102
28
14.4
103
38
17.4
107
48
24.0
115
9
9.3
98
19
12.4
102
29
14.8
104
39
17.8
107
10
9.8
98
20
12.6
102
30
15.1
104
40
18.2
107
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 8 и 5 равных частичных интервалов соответственно.