Вариант №15
Из партии в 11 деталей, содержащей 4 бракованных, наудачу выбраны 5 деталей. Найти вероятность того, что среди них будет обнаружено ровно две бракованные детали.
В урне 3 чёрных и 7 красных шаров. Найти вероятность того, что среди наудачу извлеченных пяти шаров окажется не менее трёх красных.
Найти вероятность надежной работы функциональной схемы, изображенной на ри-
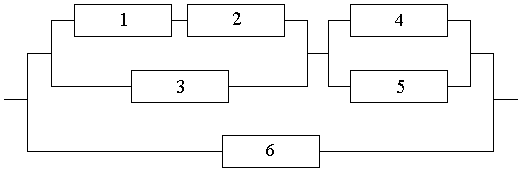
сунке, если вероятность выхода из строя каждого из её независимо работающих элементов равна 0.005.
На двух станках обрабатываются однотипные детали. Вероятность изготовления стандартной детали для станка №1 равна 0.96, а для станка №2 – 0.92. Детали складываются в одном месте, причем станок №1 изготавливает в 1.5 раза меньше деталей, чем станок №2. Найти вероятность того, что взятая наудачу деталь окажется нестандартной.
Пусть вероятность того, что наудачу взятая деталь нестандартна, равна 0.1. Найти вероятность того, что среди пяти взятых наудачу деталей окажется не более двух нестандартных.
На участке девяносто станков. Вероятность надежной работы каждого из них – 0.85. Найти вероятность того, что в данный момент работает менее восьмидесяти из них; ровно 80 станков.
Вероятность изготовления нестандартной детали равна 0.004. Найти вероятность того, что среди 1000 деталей окажется не менее трех нестандартных деталей.
В урне находится 7 красных шаров и 5 черных, одинаковых наощупь. Наудачу извлекаются 3 шара. Составить ряд распределения дискретной случайной величины X – числа красных шаров среди отобранных. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого ряда и отобразить их на многоугольнике распределения.
Случайная величина X задана плотностью вероятностей:
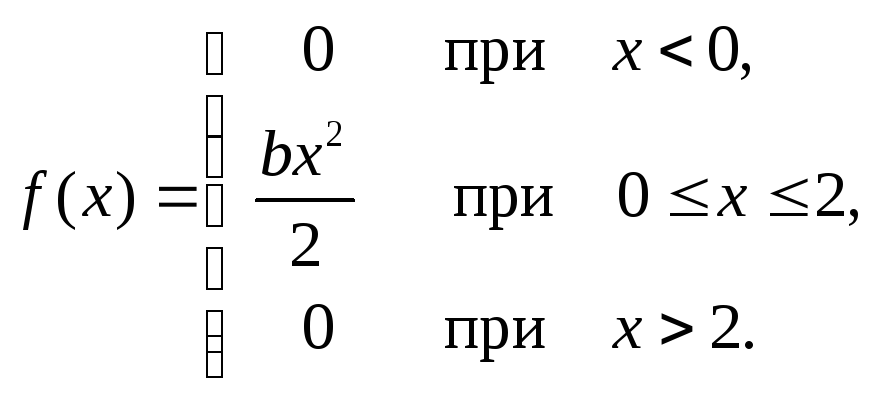
Найти коэффициент b, функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность P(0<X<1). Построить графики плотности и функции распределения и на показать них математическое ожидание и среднее квадратическое отклонение σ(X).
Диаметр детали – случайная величина, распределенная по нормальному закону с параметрами a = 50 мм, σ = 0.2 мм. Найти вероятность того, что диаметр наудачу взятой детали из партии составит от 49.5 мм до 50.4 мм; отличается от a не более, чем на 0.3 мм. Какое отклонение диаметра от a можно гарантировать с вероятностью 0.97? В каком интервале с вероятностью 0.9973 будут заключены диаметры всех изготовленных деталей?
На основе данных о результатах тестирования 49-ти студентов по дисциплине "Математика" (по двадцатибальной системе) сформировать таблицу значений относи-
-
№
Балл
№
Балл
№
Балл
№
Балл
№
Балл
1
7.3
11
9.3
21
10.3
31
11.0
41
11.8
2
7.5
12
9.4
22
10.3
32
11.1
42
11.9
3
7.7
13
9.5
23
10.4
33
11.2
43
12.0
4
7.9
14
9.6
24
10.4
34
11.3
44
12.1
5
8.2
15
9.7
25
10.5
35
11.4
45
12.2
6
8.4
16
9.8
26
10.6
36
11.5
46
12.3
7
8.6
17
9.9
27
10.8
37
11.5
47
12.4
8
8.8
18
10.1
28
10.9
38
11.6
48
12.5
9
8.9
19
10.2
29
10.9
39
11.7
49
12.6
10
9.2
20
10.2
30
11.0
40
11.8
тельных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
7.3
11.0
11
9.3
14.5
21
10.3
15.7
31
11.0
16.6
41
11.8
17.9
2
7.5
11.4
12
9.4
14.7
22
10.3
15.8
32
11.1
16.6
42
11.9
18.1
3
7.7
11.8
13
9.5
15.1
23
10.4
15.8
33
11.2
16.7
43
12.0
18.3
4
7.9
12.2
14
9.6
15.2
24
10.4
15.9
34
11.3
16.8
44
12.1
18.5
5
8.2
12.8
15
9.7
15.3
25
10.5
16.1
35
11.4
16.8
45
12.2
18.7
6
8.4
13.2
16
9.8
15.3
26
10.6
16.2
36
11.5
16.9
46
12.3
19.2
7
8.6
13.5
17
9.9
15.5
27
10.8
16.3
37
11.5
17.0
47
12.4
19.6
8
8.8
13.7
18
10.1
15.5
28
10.9
16.4
38
11.6
17.3
48
12.5
20.0
9
8.9
14.0
19
10.2
15.6
29
10.9
16.5
39
11.7
17.5
49
12.6
21.0
10
9.2
14.3
20
10.2
15.7
30
11.0
16.5
40
11.8
17.7
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 7 и 6 равных частичных интервалов соответственно.