Вариант №28
В розыгрыше первенства по баскетболу участвуют 18 команд, из которых случайным образом формируются 2 группы по 9 команд. Среди них имеется 6 команд экстра-класса. Найти вероятность того, что в каждую группу попадут по 3 команды экстра-класса.
Устройство состоит из 4-х независимых узлов. Вероятность отказа первого узла равна 0.1, второго – 0.12, третьего – 0.15, а четвёртого – 0.2. Найти вероятность надежной работы двух узлов из четырёх; трех узлов из четырёх.
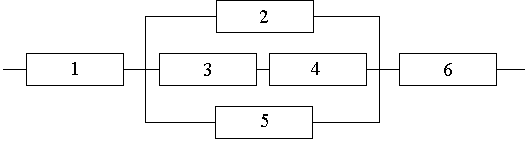
Вероятность надежной (безотказной) работы каждого из элементов функциональной цепи равна 0.8. Найти вероятность отказа цепи, изображенной на рисунке.
На сборку поступают детали 4-х типов. Деталей 1-го типа в 1.5 раза меньше, чем деталей 2-го типа и в 2 раза меньше, чем деталей 3-го типа и столько же, сколько деталей 4-го типа. Вероятность того,что деталь 1-го типа окажется годной, равна 0.9, 2-го типа – 0.85, 3-го – 0.9 и 4-го типа – 0.75. Найти вероятность того, что наудачу взятая сборщиком деталь окажется бракованной.
Контролируется работа каждого из 10 узлов устройства. Вероятность того, что узел окажется неисправным, равна 0.2. Найти вероятность того, что не менее двух узлов окажутся исправными.
Вероятность выхода из строя конструкции при приложении расчётной нагрузки 0.05. Какова вероятность того, что из восьмисот конструкций, испытанных независимо друг от друга, не менее 550-ти выдержат нагрузку; ровно 550 выдержат нагрузку?
Найти вероятность того, что среди 2000 деталей окажется более 3-х нестандартных, если вероятность изготовления стандартной детали равна 0.998.
В партии 10 деталей, из них 7 стандартных, остальные нестандартные. Наудачу отобраны 4 детали. Составить закон распределения дискретной случайной величины X – числа нестандартных деталей среди отобранных. Построить многоугольник распределения, вычислить M(X) и σ(X) и отобразить их на многоугольнике распределения.
Случайная величина X задана плотностью вероятностей:
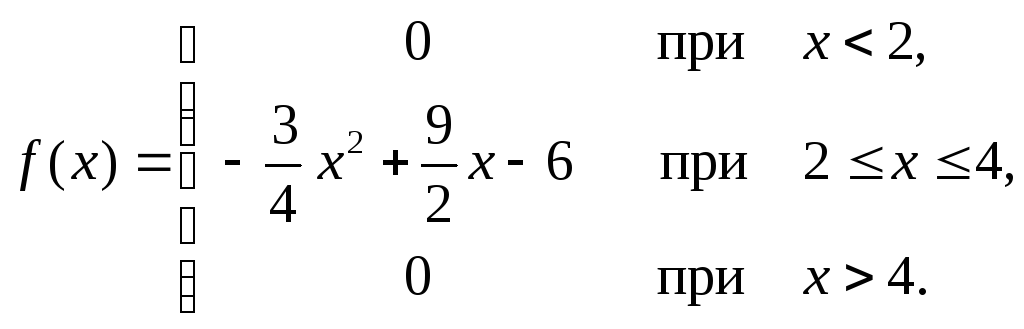
Найти функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность попадания X в интервал (3.5; 3.9). Построить графики плотности и функции распределения и на показать них M(X) и σ(X).
Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожиданием (проектная длина) a = 115 мм. Фактическая длина изготовленных деталей 114<X<116 мм. Найти вероятность того, что длина наудачу взятой детали меньше 115.5 мм. Какое отклонение длины от а можно гарантировать с вероятностью 0.95? В каких пределах с вероятностью 0.9973 будут заключены длины изготовленных деталей?
На основе данных о результатах определения степени истероидности поведения 50-ти подростков сформировать таблицу значений относительных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот
-
№
И [%]
№
И [%]
№
И [%]
№
И [%]
№
И [%]
1
10.1
11
11.8
21
13.1
31
14.4
41
15.9
2
10.5
12
11.9
22
13.2
32
14.6
42
16.0
3
10.7
13
12.1
23
13.3
33
14.8
43
16.2
4
10.9
14
12.2
24
13.4
34
15.1
44
16.4
5
11.0
15
12.3
25
13.5
35
15.2
45
16.8
6
11.1
16
12.4
26
13.6
36
15.4
46
16.9
7
11.2
17
12.6
27
13.7
37
15.5
47
17.2
8
11.3
18
12.7
28
13.9
38
15.6
48
17.4
9
11.4
19
12.9
29
14.0
39
15.7
49
17.6
10
11.5
20
13.0
30
14.2
40
15.8
50
17.8
и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 6 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
10.1
49.0
11
11.8
62.6
21
13.1
67.0
31
14.4
69.4
41
15.9
72.7
2
10.5
51.5
12
11.9
63.2
22
13.2
67.4
32
14.6
69.6
42
16.0
73.3
3
10.7
53.5
13
12.1
63.7
23
13.3
67.8
33
14.8
69.8
43
16.2
74.5
4
10.9
55.0
14
12.2
64.2
24
13.4
68.0
34
15.1
70.2
44
16.4
75.5
5
11.0
56.0
15
12.3
64.6
25
13.5
68.2
35
15.2
70.6
45
16.8
76.5
6
11.1
57.5
16
12.4
65.0
26
13.6
68.4
36
15.4
71.0
46
16.9
77.5
7
11.2
59.0
17
12.6
65.2
27
13.7
68.6
37
15.5
71.4
47
17.2
79.0
8
11.3
60.0
18
12.7
65.6
28
13.9
68.8
38
15.6
71.8
48
17.4
81.1
9
11.4
61.0
19
12.9
66.2
29
14.0
69.0
39
15.7
72.0
49
17.6
89.5
10
11.5
61.7
20
13.0
66.6
30
14.2
69.2
40
15.8
72.3
50
17.8
94.7
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 6 и 7 равных частичных интервалов соответственно.