Вариант №20
В партии из 15-ти изделий есть пять бракованных. Семь наудачу выбранных изделий подвергаются контролю. Найти вероятность того, что среди проверяемых изделий будет обнаружено ровно два бракованных.
В урне 8 синих и 7 красных шаров. Найти вероятность того, что среди девяти наудачу извлеченных шаров окажется более шести синих.
Вероятность надёжной работы независимо работающих элементов каждой цепи одинакова и равна p = 0.8. Определить, какая из этих двух цепей надежнее.
В двух урнах находятся шары. В первой – 9 красных и 8 синих, во второй – 11 красных и 6 синих. Из первой урны вынут один шар и переложен во вторую. Затем из второй урны извлекается наудачу один шар. Найти вероятность того, что это будет синий шар.
В типографии четыре машины. Вероятность надежной работы каждой из них – 0.9. Найти вероятность того, что в данный момент в типографии работает не менее трех машин.
Вероятность того, что наудачу взятая деталь из партии стандартна, равна 0.92. Найти вероятность того, что среди взятых наудачу шестисот деталей не менее пятидесяти окажутся нестандартными; ровно 50 деталей окажутся нестандартными.
Вероятность неточной сборки прибора равна 0.004. Найти вероятность того, что среди 500 приборов окажется более четырех неточно собранных.
В урне 6 белых и 2 черных шара. Наудачу извлечены пять шаров. Составить ряд распределения дискретной случайной величины X – числа белых шаров среди извлеченных. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого ряда и отобразить их на многоугольнике распределения.
Плотность вероятностей f(x) некоторой непрерывной случайной величины X задана г
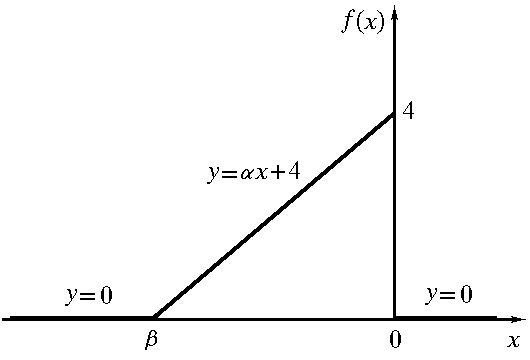рафически.
Найти коэффициентыα
и β,
записать выражение для f(x),
найти функцию распределения F(x),
математическое ожидание M(X),
среднее квадратическое отклонение
σ(X)
и вероятность P(-3<X<0).
Построить график функции распределения
и показать на нём и на графике функции
плотности вероятностей f(x)
математическое ожидание M(X)
и среднее квадратическое отклонение
σ(X).Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожиданием (проектная длина) a = 1258 мм. Фактическая длина изготовленных деталей находится в пределах 1257 ÷ 1259 мм. Найти вероятность того, что длина наудачу взятой детали будет больше 1257.2 мм. Какое отклонение длины детали от a можно гарантировать с вероятностью 0.91? В каких пределах с вероятностью 0.9973 будут заключены длины изготовленных деталей?
На основе данных о результатах 50-ти измерений отклонения толщины листа от номинального размера сформировать таблицу значений относительных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных
-
№
h [мк]
№
h [мк]
№
h [мк]
№
h [мк]
№
h [мк]
1
-2.5
11
1.2
21
3.6
31
6.4
41
9.5
2
-2.2
12
1.4
22
3.8
32
6.6
42
10.6
3
-2.1
13
1.5
23
4.3
33
7.0
43
10.9
4
-1.8
14
1.8
24
4.6
34
7.3
44
11.2
5
-1.6
15
2.0
25
4.9
35
7.4
45
11.5
6
-1.4
16
2.1
26
5.4
36
7.7
46
11.8
7
-0.2
17
2.5
27
5.6
37
8.0
47
12.0
8
0.4
18
2.8
28
5.7
38
8.2
48
12.3
9
0.6
19
3.0
29
6.0
39
8.7
49
12.8
10
1.0
20
3.4
30
6.2
40
9.1
50
13.4
частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 6 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
-2.5
144.1
11
1.2
145.0
21
3.6
145.3
31
6.4
145.5
41
9.5
145.9
2
-2.2
144.4
12
1.4
145.1
22
3.8
145.3
32
6.6
145.5
42
10.6
145.9
3
-2.1
144.5
13
1.5
145.1
23
4.3
145.4
33
7.0
145.5
43
10.9
145.9
4
-1.8
144.6
14
1.8
145.1
24
4.6
145.4
34
7.3
145.6
44
11.2
146.0
5
-1.6
144.7
15
2.0
145.2
25
4.9
145.4
35
7.4
145.6
45
11.5
146.0
6
-1.4
144.7
16
2.1
145.2
26
5.4
145.4
36
7.7
145.6
46
11.8
146.1
7
-0.2
144.8
17
2.5
145.2
27
5.6
145.4
37
8.0
145.6
47
12.0
146.2
8
0.4
144.9
18
2.8
145.2
28
5.7
145.4
38
8.2
145.7
48
12.3
146.4
9
0.6
144.9
19
3.0
145.3
29
6.0
145.4
39
8.7
145.7
49
12.8
146.7
10
1.0
144.9
20
3.4
145.3
30
6.2
145.5
40
9.1
145.7
50
13.4
147.0
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 6 и 7 равных частичных интервалов соответственно.