
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант №20
- •Вариант №21
- •Вариант №22
- •Вариант №23
- •Вариант №24
- •Вариант №25
- •Вариант №26
- •Вариант №27
- •Вариант №28
- •Вариант №29
- •Вариант №30
Вариант №23
Партия содержит 12 изделий, из которых половину подвергают контролю. Найти вероятность того, что среди них будет обнаружено ровно два бракованных изделия, если число бракованных изделий во всей партии равно три.
Прибор состоит из 3-х независимо работающих узлов, каждый из которых может в течение времени T выйти из строя. Вероятность безотказной работы за время T первого узла равна p1 = 0.8; второго – p2 = 0.9; третьего – p3 = 0.7. Найти вероятность того, что за время T выйдут из строя ровно 2 узла; хотя бы 1 узел; все 3 узла.
Найти вероятность отказа функциональной цепи, изображенной на рисунке, если ве-
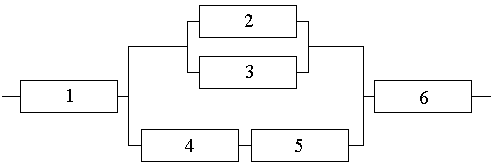
роятность надежной работы каждого элемента одна и та же и равна p = 0.93.
В 4-х урнах белые и черные шары, одинаковые на ощупь. В первой – 3 белых и 1 черный шар, во второй – 6 белых и 4 черных, в третьей – 9 белых и 1 черный, в четвертой – 2 белых и 5 черных. Из наудачу выбранной урны случайным образом вынимается один шар. Найти вероятность того, что он белый.
Из большой партии деталей отбирают для контроля 10 штук. Доля нестандартных деталей во всей партии составляет 15%. Найти вероятность того, что не более 2-х деталей окажутся стандартными.
Из партии деталей отобраны для контроля 800 штук. Известно, что доля нестандартных деталей во всей партии составляет 25%. Найти вероятность того, что не менее 650 деталей окажутся стандартными; ровно 650 деталей окажутся стандартными.
Автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0.004. Найти вероятность того, что среди 1000 деталей будет не менее трех бракованных.
Устройство состоит из 3-х элементов, работающих независимо. Вероятность отказа в одном испытании равна 0.15. Составить закон распределения дискретной случайной величины X – числа отказавших элементов в одном испытании. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.
П
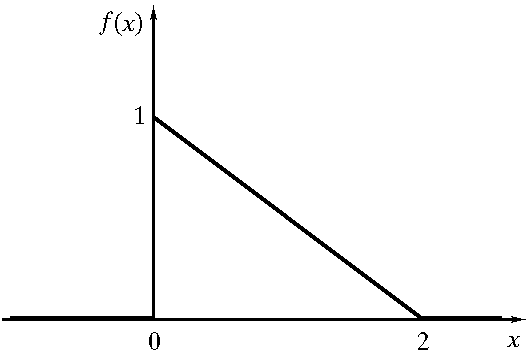 лотность
вероятностейf(x)
некоторой непрерывной случайной
величины X
задана графически. Записать выражение
для плотности распределения f(x),
найти функ-цию распределения F(x),
математическое ожидание M(X),
среднее квадратическое отклонение
σ(X)
и вероятность P(0<X<0.5).
Построить график функции распределения
и показать на нём и на графике плотности
вероятностей f(x)
математическое ожидание и среднее
квадратическое отклонение σ(X).
лотность
вероятностейf(x)
некоторой непрерывной случайной
величины X
задана графически. Записать выражение
для плотности распределения f(x),
найти функ-цию распределения F(x),
математическое ожидание M(X),
среднее квадратическое отклонение
σ(X)
и вероятность P(0<X<0.5).
Построить график функции распределения
и показать на нём и на графике плотности
вероятностей f(x)
математическое ожидание и среднее
квадратическое отклонение σ(X).На станке изготавливается деталь. Ее длина X – случайная величина, распределенная по нормальному закону с параметрами: a = 2500 см, σ = 2 см. Найти вероятность того, что длина детали заключена между 2497 и 2504 см. Какое отклонение длины детали от a можно гарантировать с вероятностью 0.85, 0.95? В каких пределах будут лежать практически все размеры деталей?
На основе данных о результатах измерений веса 49-ти пачек макарон "Vegeta" сформировать таблицу значений относительных частот для равноотстоящих вариант, таб-
-
№
P [Гр]
№
P [Гр]
№
P [Гр]
№
P [Гр]
№
P [Гр]
1
898
11
909
21
913
31
917
41
921
2
901
12
910
22
914
32
917
42
922
3
903
13
910
23
914
33
918
43
923
4
904
14
911
24
915
34
918
44
924
5
905
15
911
25
916
35
919
45
925
6
906
16
911
26
916
36
919
46
926
7
907
17
912
27
916
37
920
47
927
8
908
18
912
28
916
38
920
48
928
9
908
19
913
29
917
39
920
49
930
10
909
20
913
30
917
40
921
лицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
898
8.2
11
909
10.1
21
913
11.3
31
917
12.7
41
921
14.4
2
901
8.4
12
910
10.2
22
914
11.4
32
917
12.8
42
922
14.5
3
903
8.6
13
910
10.3
23
914
11.5
33
918
13.0
43
923
14.7
4
904
8.7
14
911
10.4
24
915
11.6
34
918
13.2
44
924
14.9
5
905
8.8
15
911
10.5
25
916
11.7
35
919
13.6
45
925
15.2
6
906
8.9
16
911
10.6
26
916
11.9
36
919
13.7
46
926
15.3
7
907
9.0
17
912
10.7
27
916
12.0
37
920
13.9
47
927
15.4
8
908
9.2
18
912
11.0
28
916
12.2
38
920
14.0
48
928
15.6
9
908
9.6
19
913
11.1
29
917
12.3
39
920
14.1
49
930
15.8
10
909
9.8
20
913
11.2
30
917
12.5
40
921
14.3
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 7 и 6 равных частичных интервалов соответственно.
