Вариант №14
В комплекте из 16-ти деталей имеются 4 детали с дефектами. Девять отобранных наудачу деталей подвергаются контролю. Найти вероятность того, что среди них будет обнаружено ровно две детали с дефектами.
В урне 8 чёрных и 4 жёлтых шара. Найти вероятность того, что среди наудачу извлечённых 4-х шаров окажется не более двух жёлтых.
Какая из двух функциональных схем надежнее, если вероятность выхода из строя
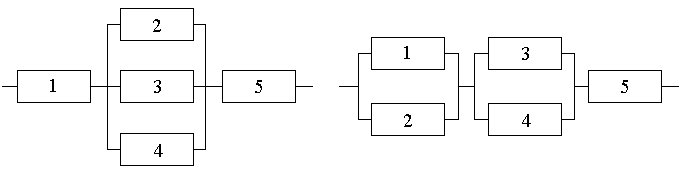
каждого отдельного элемента схемы равна 0.1?
В двух урнах содержатся шары. В первой – 8 белых и 12 чёрных, во второй – 9 белых и 11 чёрных. Из первой урны извлекаются 3 шара, из второй – 5, а затем из этих восьми шаров извлечен один. Найти вероятность того, что он окажется белым.
В приборе стоят 6 независимо работающих предохранителей. Для каждого из них вероятность перегореть после 1 000 часов работы равна 0.4. Если перегорело не менее 4-х предохранителей, то прибор требует ремонта. Найти вероятность того, что прибор потребует ремонта после 1 000 часов работы.
Испытывается каждый из 150-ти элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0.9. Найти вероятность того, что выдержат испытание более 120-ти элементов; ровно 120 элементов.
Вероятность изготовления нестандартной делали равна 0.005. Найти вероятность того, что среди 1000 деталей окажется более двух нестандартных.
ОТК проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0.8. В проверяемой партии 4 изделия. Составить закон распределения X – числа нестандартных изделий среди четырех проверяемых. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.
Случайная величина X задана плотностью вероятностей:
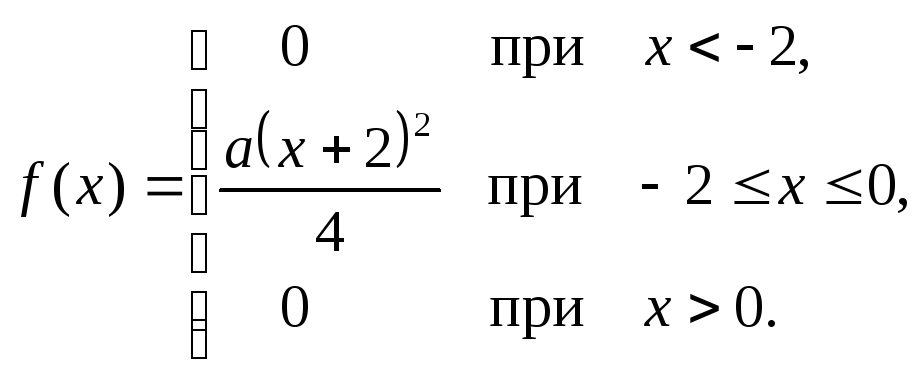
Найти коэффициент a, функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность P(-1<X<0). Построить графики плотности и функции распределения и показать на них математическое ожидание и среднее квадратическое отклонение σ(X).
Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожиданием (проектная длина) a = 140 мм. Фактическая длина изготовленных деталей находится в диапазоне 138<X<142 мм. Найти вероятность того, что длина наудачу взятой детали будет больше 141 мм. Какое отклонение длины детали от a можно гарантировать с вероятностью 0.95? В каких пределах с вероятностью 0.9973 будут заключены длины всех проверенных деталей?
На основе данных о результатах измерений веса тела у 48-ми подростков 14-ти лет
-
№
P [кГ]
№
P [кГ]
№
P [кГ]
№
P [кГ]
№
P [кГ]
1
29.8
11
43.7
21
49.4
31
53.0
41
59.5
2
31.5
12
44.3
22
49.8
32
53.5
42
61.0
3
33.5
13
44.8
23
50.2
33
54.0
43
62.0
4
35.0
14
45.5
24
50.6
34
54.5
44
63.5
5
37.0
15
46.3
25
51.0
35
55.0
45
64.5
6
38.5
16
46.8
26
51.4
36
55.5
46
66.0
7
39.5
17
47.8
27
51.7
37
56.0
47
68.0
8
41.0
18
48.2
28
51.9
38
56.6
48
70.0
9
42.0
19
48.6
29
52.1
39
57.3
10
43.2
20
49.0
30
52.3
40
58.5
мужского пола сформировать таблицу значений относительных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 8 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
29.8
3.0
11
43.7
8.1
21
49.4
9.6
31
53.0
10.6
41
59.5
12.1
2
31.5
4.1
12
44.3
8.3
22
49.8
9.7
32
53.5
10.7
42
61.0
12.2
3
33.5
5.5
13
44.8
8.5
23
50.2
9.8
33
54.0
10.8
43
62.0
12.4
4
35.0
6.0
14
45.5
8.7
24
50.6
9.9
34
54.5
10.9
44
63.5
12.6
5
37.0
6.4
15
46.3
8.9
25
51.0
10.0
35
55.00
10.9
45
64.5
12.8
6
38.5
7.1
16
46.8
9.1
26
51.4
10.1
36
55.5
11.1
46
66.0
13.4
7
39.5
7.3
17
47.8
9.2
27
51.7
10.2
37
56.0
11.3
47
68.0
14.2
8
41.0
7.5
18
48.2
9.3
28
51.9
10.3
38
56.6
11.5
48
70.0
14.9
9
42.0
7.7
19
48.6
9.4
29
52.1
10.4
39
57.3
11.6
10
43.2
7.9
20
49.0
9.5
30
52.3
10.5
40
58.5
11.9
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 8 и 5 равных частичных интервалов соответственно.