Вариант №25
В ящике лежат 5 красных, 7 синих и 6 зеленых шаров, одинаковых на ощупь. Наудачу извлекаются 6 шаров. Какова вероятность того, что будут вынуты 1 зеленый, 2 синих и 3 красных шара?
Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,8. Найти вероятность того, что из двух проверенных изделий только одно стандартно.
Вероятность выхода из строя каждого элемента функциональной схемы равна q = 0.05. Определить, какая из двух цепей надежнее.
В пирамиде установлены 5 винтовок, из которых 3 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при первом выстреле из винтовки с прицелом равна 0.95, для винтовки без оптического прицела эта вероятность равна 0.7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
Электрическая цепь состоит из 6 параллельно включенных потребителей. Вероятность отказа каждого из них равна 2/5, а взаимное влияние в цепи отсутствует. Найти вероятность того, что откажет не менее половины потребителей.
На заводе-автомате 800 станков. Вероятность отказа каждого из них 0.1. Найти вероятность того, что в данный момент времени работает не менее 700 станков; ровно 700 станков.
Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течение времени t равна 0.002. Найти вероятность того,что за это время откажут более двух элементов.
Устройство состоит из 4-х элементов, работающих независимо. Вероятность надежной работы каждого элемента в одном испытании равна 0.9. Составить закон распределения случайной величины X – числа отказавших элементов в одном опыте. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.
П
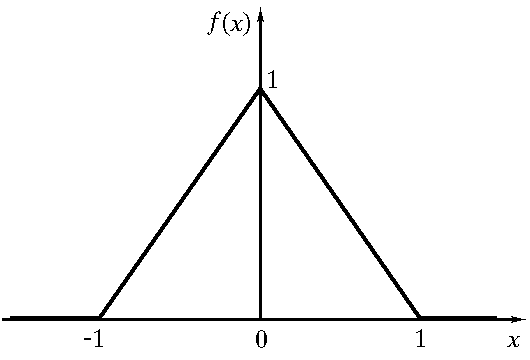лотность
вероятностейf(x)
некоторой непрерывной случайной
величины X задана графически. Записать
выражение для плотности распределения
f(x),
найти функ-цию распределения F(x),
математическое ожидание M(X),
среднее квадратическое отклонение
σ(X)
и вероятность P(0<X<0.5).
Построить график функции распределения
и показать на нём и на графике плотности
вероятности f(x)
математическое ожидание M(X)
и среднее квадратическое отклонение
σ(X).Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожиданием (проектная длина) a = 1960 мм. Фактическая длина изготовленных деталей не менее 1954 мм и не более 1966 мм. Найти вероятность того, что длина наудачу взятой детали больше 1961 мм. Какое отклонение длины детали от a можно гарантировать с вероятностью 0.91? В каких пределах с вероятностью 0.9973 будут заключены длины изготовленных деталей?
На основе данных о результатах анализа эффективности работы 47-ми предприятий города по изменению реальной заработной платы каждого работающего в отчетном
-
№
Эр [%]
№
Эр [%]
№
Эр [%]
№
Эр [%]
№
Эр [%]
1
91
11
100
21
102
31
104
41
108
2
93
12
100
22
102
32
104
42
109
3
95
13
101
23
103
33
105
43
109
4
96
14
101
24
103
34
105
44
110
5
97
15
101
25
103
35
106
45
111
6
97
16
101
26
103
36
106
46
112
7
97
17
101
27
103
37
106
47
113
8
97
18
102
28
103
38
107
9
98
19
102
29
104
39
107
10
98
20
102
30
104
40
107
году (в % к предыдущему году) сформировать таблицу значений относительных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
91
23.0
11
100
16.6
21
102
13.8
31
104
11.6
41
108
7.6
2
93
21.6
12
100
16.2
22
102
13.6
32
104
11.4
42
109
6.9
3
95
2.08
13
101
15.9
23
103
13.4
33
105
11.2
43
109
6.0
4
96
2.02
14
101
15.7
24
103
13.2
34
105
11.0
44
110
5.3
5
97
19.6
15
101
15.5
25
103
13.0
35
106
10.7
45
111
4.1
6
97
18.6
16
101
15.3
26
103
12.8
36
106
10.3
46
112
3.2
7
97
18.2
17
101
15.1
27
103
12.6
37
106
9.9
47
113
2.6
8
97
17.8
18
102
14.8
28
103
12.4
38
107
9.3
9
98
17.4
19
102
14.4
29
104
12.2
39
107
8.8
10
98
16.9
20
102
14.0
30
104
11.9
40
107
8.2
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 7 и 6 равных частичных интервалов соответственно.