Вариант №11
Для проведения лабораторных работ группа студентов, в которой 10 юношей и 6 девушек, произвольным образом делится на две равные подгруппы. Найти вероятность того, что в каждой подгруппе окажется по одинаковому числу девушек.
На книжной полке имеется 8 журналов, из которых 5 в переплете. Наудачу взяты 4 журнала. Найти вероятность того, что среди них окажется не менее трех в переплете.
Найти вероятность надежной работы функциональной схемы, состоящей из шести
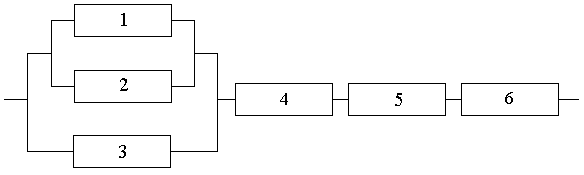
элементов, если вероятности отказа каждого из элементов равны: q1 = 0.03, q2 = 0.05, q3 = q4 = 0.04, q5 = q6 = 0.02.
В двух урнах имеются шары: в первой – 7 красных и 5 желтых, во второй – 10 красных и 4 желтых. Из первой урны извлекаются 2 шара, а из второй – 3 шара. Затем из этих 5 шаров наудачу извлекается один шар. Найти вероятность того, что этот шар красный.
Автобаза обслуживает 12 магазинов. От каждого из них заявка на автомашины на следующий день может поступить с вероятностью 0.4. Найти вероятность того, что поступит не более 9-ти заявок.
В системе установлено 600 независимо работающих предохранителей. Для каждого из них вероятность выхода из строя после 10 000 часов работы равна 0.2. Если вышло из строя не менее 110 предохранителей, то система требует ремонта. Найти вероятность того, что система потребует ремонта после 10 000 часов работы.
Радиоаппаратура состоит из 800 элементов. Вероятность отказа одного элемента в течение года работы равна 0.005 и не зависит от состояния других элементов. Какова вероятность отказа двух элементов за год; более двух элементов за год?
В коробке находятся 5 деталей первого сорта и 3 – второго сорта. Составить закон распределения дискретной случайной величины X – числа деталей второго сорта среди четырёх отобранных. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.
Дифференциальная функция f(x) случайной величины X равна:
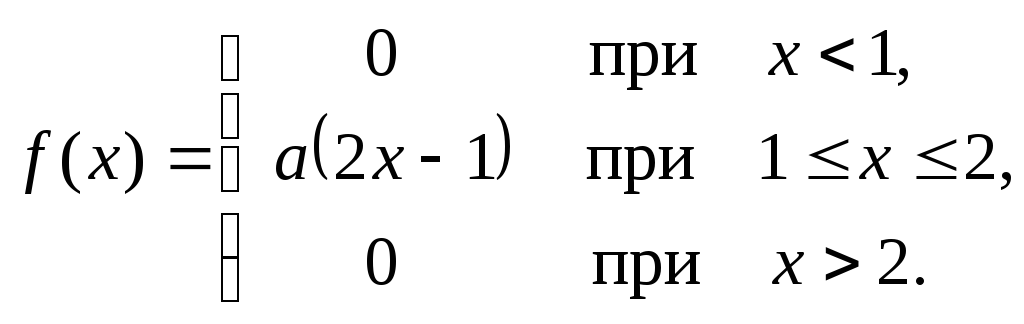
Найти коэффициент a, интегральную функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность P(1<X<1.5). Построить графики плотности и функции распределения и на показать них математическое ожидание и среднее квадратическое отклонение σ(X).
Автомат штампует детали. Контролируется длина X, которая распределена по нормальному закону с математическим ожиданием (проектная длина) a = 135 мм. Фактическая длина изготовленных деталей 134.7<X<135.3 мм. Найти вероятность того, что длина наудачу взятой детали меньше 134.9 мм. Какое отклонение длины детали от a можно гарантировать с вероятностью 0.96? В каких пределах с вероятностью 0.9973 будут заключены длины изготовленных деталей?
На основе данных о результатах 49-ти измерений содержания солода в пиве "Балтика" №6 сформировать таблицу значений относительных частот для равноотстоящих
-
№
c [%]
№
c [%]
№
c [%]
№
c [%]
№
c [%]
1
3.5
11
8.2
21
9.6
31
10.6
41
12.1
2
4.5
12
8.4
22
9.7
32
10.7
42
12.3
3
5.8
13
8.6
23
9.8
33
10.8
43
12.5
4
6.2
14
8.8
24
9.9
34
10.9
44
12.7
5
6.8
15
9.4
25
10.0
35
11.0
45
12.9
6
7.2
16
9.1
26
10.1
36
11.2
46
13.8
7
7.4
17
9.2
27
10.2
37
11.4
47
14.5
8
7.6
18
9.3
28
10.3
38
11.5
48
15.3
9
7.8
19
9.4
29
10.4
39
11.8
49
15.9
10
8.0
20
9.5
30
10.5
40
12.0
вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
3.5
1.0
11
8.2
8.0
21
9.6
10.9
31
10.6
13.5
41
12.1
16.4
2
4.5
2.0
12
8.4
8.4
22
9.7
11.1
32
10.7
13.7
42
12.3
16.8
3
5.8
3.5
13
8.6
8.7
23
9.8
11.3
33
10.8
14.0
43
12.5
17.1
4
6.2
5.2
14
8.8
8.9
24
9.9
11.5
34
10.9
14.3
44
12.7
17.5
5
6.8
5.6
15
9.4
9.2
25
10.0
11.7
35
11.0
14.5
45
12.9
18.1
6
7.2
6.0
16
9.1
9.6
26
10.1
11.9
36
11.2
14.7
46
13.8
18.7
7
7.4
6.4
17
9.2
10.1
27
10.2
12.2
37
11.4
15.2
47
14.5
19.3
8
7.6
6.8
18
9.3
10.3
28
10.3
12.5
38
11.5
15.4
48
15.3
19.9
9
7.8
7.2
19
9.4
10.5
29
10.4
12.8
39
11.8
15.8
49
15.9
20.8
10
8.0
7.6
20
9.5
10.7
30
10.5
13.2
40
12.0
16.1
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 7 и 6 равных частичных интервалов соответственно.