Вариант №21

1. В партии из 14 изделий 5 – бракованных, 7 наудачу выбранных изделий из партии подвергаются контролю. Найти вероятность того, что среди них будет обнаружено 3 бракованных изделия.

2. В коробке лежат 12 белых и 8 красных шаров, одинаковых на ощупь. Вынули 8 шаров. Какова вероятность того, что красных шаров вынуто не более двух?

3. Найти вероятность выхода из строя функциональной цепи, показанной на рисунке,

если вероятность надежной работы каждого элемента одна и та же, и равна p = 0.93.

4. В вычислительной лаборатории имеются 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0.95; для полуавтомата эта вероятность равна 0.8. Студент производит расчет на наудачу выбранной машине. Чему равна вероятность того, что до окончания расчета машина не выйдет из строя?

5. Из партии деталей отобраны для контроля 12 штук. Известно, что доля стандартных деталей во всей партии составляет 75%. Найти вероятность того, что более 9 деталей окажутся стандартными.

6. Электрическая цепь состоит из 600 параллельно включенных потребителей. Вероятность отказа каждого из них равна 2/5, а взаимное влияние в цепи отсутствует. Найти вероятность того, что откажет не менее 30-ти потребителей; ровно 30 потребителей.

7. Вероятность изготовления бракованной детали равна 0.002. Найти вероятность того, что среди 1000 деталей окажется не менее 3 бракованных.

8. В партии 10% нестандартных деталей. Наудачу отобраны 4 детали. Написать закон распределения дискретной величины X – числа нестандартных деталей среди отобранных. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.

9. Ф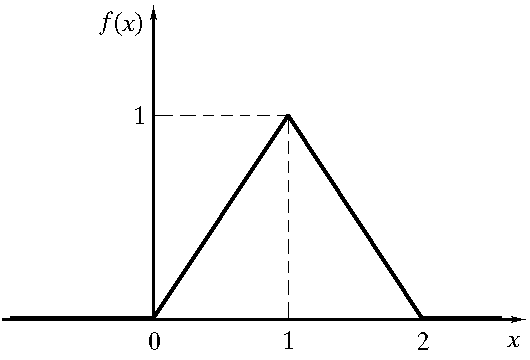ункция плотности распределенияf(x) некоторой непрерывной случайной величины X задана графически. Записать выражение для плотности распределения f(x), найти функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность P(1.5<X<2). Построить график функции распределения F(x) и показать на нём и на графике функции плотности рас-пределения f(x) математическое ожидание и среднее квадратическое отклонение σ(X).

10. Диаметр изготовляемой в цехе партии деталей является случайной величиной, распределенной по нормальному закону с параметрами: a = 45 мм, σ = 0.1 мм. Найти вероятность того, что диаметр наудачу взятой детали составляет от 44.8 до 45.1 мм, отличается от a не более, чем на 0.15 мм. Какое отклонение диаметра детали от a можно гарантировать с вероятностью 0.96? В каком интервале с вероятностью 0.9973 будут заключены диаметры всех деталей?

11. На основе данных о результатах определения уровня доминантности (настойчивости, напористости) у 47-ми детей сформировать таблицу значений относительных частот

№	E+ [б/р]	№	E+ [б/р]	№	E+ [б/р]	№	E+ [б/р]	№	E+ [б/р]
1	344.0	11	345.0	21	345.3	31	345.5	41	345.8
2	344.3	12	345.0	22	345.3	32	345.5	42	345.9
3	344.5	13	345.1	23	345.3	33	345.5	43	345.9
4	344.6	14	345.1	24	345.4	34	345.6	44	346.0
5	344.7	15	345.2	25	345.4	35	345.6	45	346.1
6	344.8	16	345.2	26	345.4	36	345.6	46	346.2
7	344.8	17	345.2	27	345.4	37	345.6	47	346.2
8	344.9	18	345.2	28	345.4	38	345.7
9	344.9	19	345.3	29	345.5	39	345.8
10	345.0	20	345.3	30	345.5	40	345.8

для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равных частичных интервалов.

12. Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.

13. Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.

14. Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.

15. Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.

16. Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.

17. Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-

№	X	Y	№	X	Y	№	X	Y	№	X	Y	№	X	Y
1	344.0	1.70	11	345.0	1.47	21	345.3	1.28	31	345.5	1.14	41	345.8	0.97
2	344.3	1.63	12	345.0	1.45	22	345.3	1.26	32	345.5	1.13	42	345.9	0.95
3	344.5	1.62	13	345.1	1.44	23	345.3	1.25	33	345.5	1.12	43	345.9	0.94
4	344.6	1.60	14	345.1	1.41	24	345.4	1.24	34	345.6	1.11	44	346.0	0.92
5	344.7	1.59	15	345.2	1.37	25	345.4	1.23	35	345.6	1.10	45	346.1	0.91
6	344.8	1.57	16	345.2	1.35	26	345.4	1.22	36	345.6	1.09	46	346.2	0.89
7	344.8	1.55	17	345.2	1.33	27	345.4	1.19	37	345.6	1.08	47	346.2	0.88
8	344.9	1.53	18	345.2	1.32	28	345.4	1.18	38	345.7	1.02
9	344.9	1.51	19	345.3	1.31	29	345.5	1.17	39	345.8	1.00
10	345.0	1.49	20	345.3	1.29	30	345.5	1.15	40	345.8	0.99

нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 7 и 6 равных частичных интервалов соответственно.