Вариант №17
Комплект из 18 деталей, содержащий 6 окрашенных деталей, произ вольным образом делится на две равные части. Какова вероятность того, что в каждой части окажется по три окрашенных детали?
Вероятности того, что нужная сборщику деталь содержится в 1-ой, 2-ой, 3-ей или 4-ой коробках равны соответственно 0.85, 0.75, 0.7 и 0.7. Найти вероятность того, что нужная сборщику деталь находится более чем в двух коробках.
Найти вероятность безотказной работы функциональной схемы, состоящей из неза-
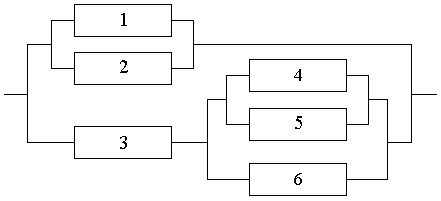
висимо работающих элементов, если вероятность отказа каждого элемента одинакова и равна q = 0.05.
Партия электрических лампочек на 20% изготовлена заводом №1, на 30% – заводом №2 и на 50% – заводом №3. Для завода №1 вероятность выпуска бракованной лампочки равна 0.01, для завода №2 – 0.005, а для завода №3 – 0.006. Какова вероятность того, что взятая наудачу лампочка окажется бракованной?
Вероятность того, что станок в течение часа потребует внимания рабочего, равна 0.4. Предполагается, что неполадки на станках независимые. Найти вероятность того, что в течение часа внимания рабочего потребуют не менее двух станков из четырех, обслуживаемых им.
Из партии деталей отобраны для контроля 220 штук. Известно, что доля стандартных деталей во всей партии составляет 85%. Найти вероятность того, что более 190 деталей окажутся стандартными; ровно 190 деталей окажутся стандартными.
Вероятность того, что изделие не выдержит испытание, равна 0.001. Найти вероятность того, что из 5000 изделий более двух не выдержат испытание.
В комплекте 80% окрашенных деталей, остальные – не окрашены. Наудачу выбраны четыре детали. Составить ряд распределения дискретной случайной величины X – числа окрашенных деталей среди отобранных. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого ряда и отобразить их на многоугольнике распределения.
Случайная величина X задана плотностью вероятностей:
Найти коэффициент c, функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность P(-0.2<X<0.5). Построить графики плотности и функции распределения и на показать них M(X) и σ(X).
На станке изготавливается деталь. Ее длина X – случайная величина, распределенная по нормальному закону с параметрами a = 23.5 см и σ = 0.2 см. Найти вероятность того, что длина детали будет заключена между 23 и 24 см. Какое отклонение длины детали от a можно гарантировать с вероятностью 0.9, 0.95? В каких пределах будут лежать размеры практически всех деталей?
На основе данных о результатах 47-ми измерений в течение суток уровня в одной из водозаборных шахт Мосводоканала сформировать таблицу значений относительных
-
№
H [см]
№
H [см]
№
H [см]
№
H [см]
№
H [см]
1
305
11
464
21
528
31
572
41
662
2
325
12
471
22
532
32
578
42
671
3
345
13
486
23
536
33
584
43
683
4
365
14
493
24
540
34
590
44
711
5
385
15
504
25
544
35
596
45
713
6
405
16
508
26
548
36
605
46
736
7
415
17
512
27
552
37
615
47
758
8
425
18
516
28
556
38
625
9
435
19
520
29
560
39
635
10
450
20
524
30
566
40
645
частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
305
138
11
464
123
21
528
115
31
572
109
41
662
96
2
325
136
12
471
122
22
532
114
32
578
108
42
671
95
3
345
135
13
486
121
23
536
114
33
584
107
43
683
93
4
365
133
14
493
120
24
540
113
34
590
106
44
711
92
5
385
131
15
504
119
25
544
113
35
596
105
45
713
91
6
405
129
16
508
119
26
548
112
36
605
104
46
736
88
7
415
128
17
512
118
27
552
112
37
615
103
47
758
84
8
425
126
18
516
117
28
556
111
38
625
101
9
435
125
19
520
116
29
560
110
39
635
100
10
450
124
20
524
116
30
566
110
40
645
98
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 7 и 6 равных частичных интервалов соответственно.