Вариант №12
У сборщика имеется 10 деталей, мало отличающихся по внешнему виду. Из них 6 деталей первого сорта, а 4 – второго. Какова вероятность того, что среди наудачу взятых 5-ти деталей окажутся три первого сорта?
В ящике 10 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что среди извлеченных деталей окажется не менее трех окрашенных.
Вероятности работы каждого из элементов функциональной цепи равны соответст-
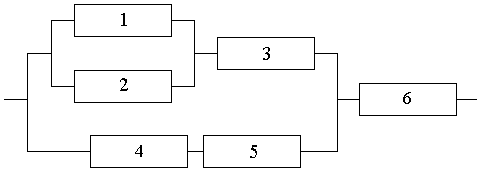
венно p1 = p2 = 0.95, p3 = 0.90, p4 = p5 = 0.85, p6 = 0.8. Найти вероятность безотказной работы этой цепи.
В двух урнах находятся шары. В первой – 6 белых и 4 черных, во второй – 8 белых и 2 черных. Извлекаются из первой урны 2 шара и из второй – один. Из этих трех шаров наудачу берётся один шар. Найти вероятность того, что последний шар белый.
Два равносильных шахматиста играют матч. Что вероятнее: выиграть не менее двух партий из четырех или не менее трех партий из пяти?
Вероятность того, что наудачу взятая деталь из партии стандартна, равна 0.8. Найти вероятность того, что среди шестисот взятых случайным образом деталей окажется не менее четырехсот стандартных; ровно 400 стандартных.
Радиоаппаратура состоит из 1000 элементов. Вероятность отказа одного элемента в течение года работы равна 0.001 и не зависит от состояния других элементов. Какова вероятность отказа не менее трех элементов за год; ровно трех элементов за год?
Вероятность попадания в цель при одном выстреле из орудия равна 0.4. Составить закон распределения X – числа промахов при пяти выстрелах. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.
Случайная величина X задана плотностью вероятностей
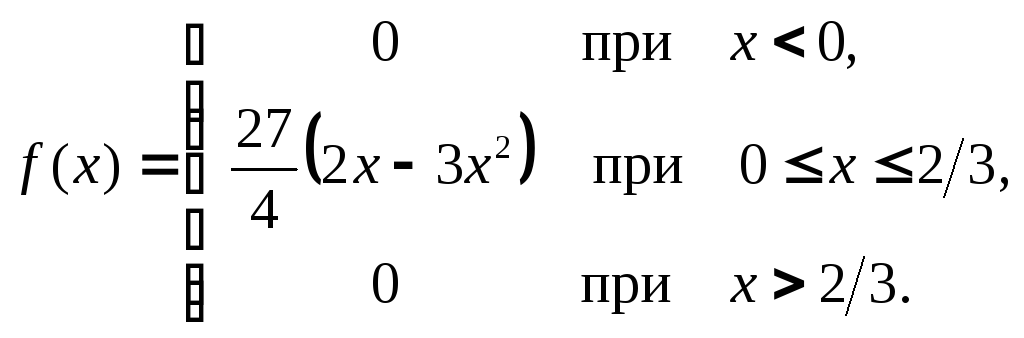
Найти интегральную функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность P(0.4<X<0.6). Построить графики плотности и функции распределения и на показать них математическое ожидание и среднее квадратическое отклонение σ(X).
На станке изготавливается деталь. Ее длина X – случайная величина, распределенная по нормальному закону с параметрами a = 22.5 см и σ = 0.3 см. Найти вероятность того, что длина детали будет заключена между 21.8 и 23.2 см. Какое отклонение длины детали от a можно гарантировать с вероятностью 0.91 и 0.99? В каких пределах, симметричных относительно a, будут лежать практически все размеры деталей?
На основе данных о результатах 50-ти измерений времени реагирования мышечной системы на внешний раздражитель сформировать таблицу значений относительных частот для равноотстоящих вариант, таблицу значений эмпирической плотности от
-
№
t [мс]
№
t [мс]
№
t [мс]
№
t [мс]
№
t [мс]
1
4.2
11
8.4
21
11.2
31
14.4
41
17.7
2
4.8
12
8.8
22
11.6
32
14.8
42
18.2
3
5.4
13
9.0
23
11.8
33
15.1
43
18.6
4
6.2
14
9.3
24
12.2
34
15.3
44
19.0
5
6.6
15
9.6
25
12.2
35
15.7
45
19.4
6
6.9
16
9.9
26
12.6
36
15.9
46
19.8
7
7.1
17
10.2
27
13.1
37
16.4
47
20.3
8
7.3
18
10.4
28
13.4
38
16.8
48
20.9
9
7.4
19
10.6
29
13.5
39
17.0
49
21.2
10
7.8
20
10.9
30
13.8
40
17.2
50
21.7
носительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 6 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01; 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
4.2
82
11
8.4
98
21
11.2
104
31
14.4
110
41
17.7
117
2
4.8
84
12
8.8
99
22
11.6
104
32
14.8
110
42
18.2
118
3
5.4
86
13
9.0
100
23
11.8
105
33
15.1
111
43
18.6
120
4
6.2
88
14
9.3
100
24
12.2
105
34
15.3
111
44
19.0
121
5
6.6
91
15
9.6
101
25
12.2
106
35
15.7
112
45
19.4
122
6
6.9
93
16
9.9
102
26
12.6
107
36
15.9
113
46
19.8
125
7
7.1
94
17
10.2
102
27
13.1
107
37
16.4
114
47
20.3
127
8
7.3
95
18
10.4
102
28
13.4
108
38
16.8
114
48
20.9
129
9
7.4
96
19
10.6
103
29
13.5
108
39
17.0
115
49
21.2
132
10
7.8
97
20
10.9
103
30
13.8
109
40
17.2
115
50
21.7
138
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 6 и 7 равных частичных интервалов соответственно.