2. . Силы трения

Характеристика силы трения покоя. Силой трения покоя называется составляющая полной реакции, лежащая в общей касательной плоскости к поверхности контакта. Модуль этой силы и ее направление зависят от внешних сил, приложенных к трущимся телам, но не могут превышать предельной силы трения покоя, под которой понимается сила трения покоя, соответствующая началу относительного движения трущихся тел.

Предельная сила трения покоя зависит от многих факторов, которые можно учесть только экспериментальным путем для каждого механизма в отдельности. При отсутствии экспериментальных данных пользуются обычно приближенными формулами, из которых наибольшее распространение имеет формула Амонтона,

F_т = f_п F, (1.17)

где F_т – модуль предельной силы трения покоя, F – модуль результирующей силы нормальных давлений на поверхности трения, f_п – коэффициент трения покоя.

Иногда употребляют формулу Кулона

F_т = А + f_п F, (1.18)

где А – сцепленность, зависящая от плотности контакта.

Характеристика силы трения скольжения. После достижения предельной силы трения покоя начинается скольжение трущихся поверхностей. Силой трения скольжения называется составляющая полной реакции для трущихся тел, лежащая в общей касательной плоскости к поверхностям контакта и направленная в сторону, противоположенную их относительному смещению.

Характеристики сил трения скольжения зависят от вида трения. В зависимости от состояния взаимодействующих тел различают: чистое трение – внешнее трение при полном отсутствии на трущихся поверхностях каких-либо посторонних примесей; сухое трение (трение несмазанных поверхностей) – внешнее трение, при котором трущиеся поверхности покрыты пленками окислов и адсорбированными молекулами газов или жидкостей, а смазка отсутствует; граничное трение – внешнее трение, при котором между трущимися поверхностями есть тонкий (порядка 0,1 мк и менее) слой смазки с обычными объемными свойствами; жидкостное (гидродинамическое) трение – трение, при котором поверхности трущихся твердых тел полностью отделены друг от друга слоем жидкости.

При сухом трении (иногда его называют кулоновым) модуль силы трения скольжения приближенно определяется по формуле, аналогичной формуле Амонтона

, (1.19)

где f – коэффициент трения скольжения, который всегда меньше коэффициента трения покоя.

Сила трения скольжения F_т направлена противоположено относительной скорости скольжения. Отсюда следует, что характеристика силы трения скольжения при сухом трении F_т в зависимости от скорости скольжения имеет вид, показанный на рис. 1.3.

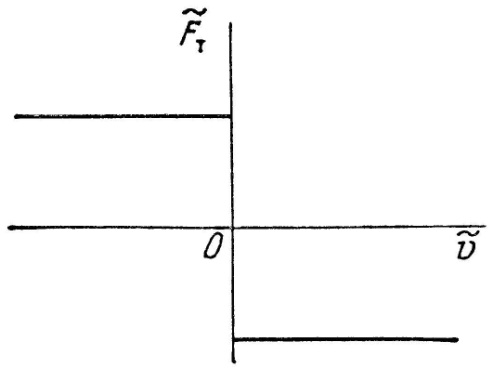
Рис. 1.3. Зависимость силы трения скольжения при сухом трении от скорости скольжения

При перемене знака скорости скольжения функция F_t( ) имеет точку разрыва, и, следовательно, эту характеристику нельзя считать линейной, несмотря на то что модуль силы трения остается постоянным. Характеристики сил с точками разрыва или излома называют существенно нелинейными, так как в этих точках нельзя определить производную и использовать обычный путь линеаризации функций посредством линейных членов ряда Тейлора.

При граничном трении уже проявляется зависимость коэффициента трения от скорости скольжения, который обычно определяется по формулам вида

, (1.20)

где f₀ – значение коэффициента трения покоя при = 0, f₁, f₂ и f₃ – экспериментальные коэффициенты, которые могут быть и положительными, и отрицательными.

При жидкостном трении сила трения определяется из формулы Ньютона

,

где – сила сдвига (внутреннего трения), которую надо приложить к слою жидкости площадью S для того, чтобы этот слой двигался относительно соседнего слоя со скоростью du при расстоянии между слоями dy. Коэффициент пропорциональности μ называется динамической вязкостью и в системе СИ имеет размерность Н·с/м² или кг/(м·с). Если производную du/dy, называемую градиентом скорости, принять равной /h, где – относительная скорость скольжения трущихся поверхностей, h – величина зазора, то формула для определения модуля силы трения F_т при жидкостном трении получает вид

или

F_т = bv, (1.21)

где b = μS/h – постоянный коэффициент, называемый коэффициентом вязкого сопротивления (кратко – коэффициентом сопротивления).

Линейная характеристика силы трения (1.21), полученная из условий жидкостного трения, справедлива только при полном разделении трущихся поверхностей слоем смазки. Однако ее часто используют при полужидкостном и даже при граничном трении из-за тех упрощений в динамических расчетах, которые дает применение линейной характеристики силы трения.

Силы трения в кинематических парах. При определении направления силы трения скольжения в кинематических парах механизма надо различать силу трения F_тij, дей­ствующую на звено i со стороны звена j, и силу трения F_тji, действующую на звено j со стороны звена i (рис. 1.4)¹. Например, для поступательной пары сила F_тij направлена противоположно скорости звена i относительно звена j, т.е. скорости v_ij, а сила F_тji – противоположно скорости v_ji.

В абсолютном движении относительно стойки сила трения может быть как силой сопротивления, так и силой движущей. В случае, показанном на рис. 1.4, при v_i > v_j сила трения F_тij есть сила сопротивления, а сила трения F_тji – движущая сила. Другими словами, звено i увлекает звено j, а звено j тормозит звено i. Сумма работ обеих сил, однако, всегда отрицательна. В рассматриваемом примере эта сумма имеет значение

.

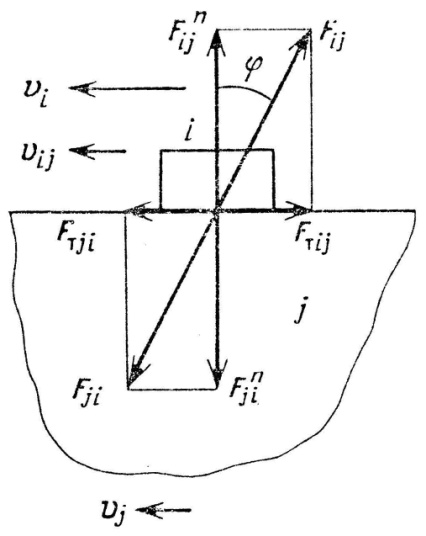
Рис. 1.4. Силы трения скольжения в плоских кинематических парах

Трение всегда сопровождается диссипацией (рассеянием) энергии, так как суммарная работа обеих сил трения (F_тij и F_тji), т.е. работа сил трения в относительном движении, переходит в тепло и рассеивается. На этом основании силы трения называют диссипативными.

Иногда силу , которая направлена по нормали к трущимся поверхностям, складывают с силой трения F_тij и получают силу F_ij, называемую полной реакцией. Угол φ, который образован реакцией F_ij с нормальной составляющей , называется углом трения. Из формулы (1.19)

, т.е. .

При малых значениях коэффициента трения угол трения φ  f.

Для вращательной пары с зазором сила трения F_тij приложена к точке касания К и направлена противоположено относительной скорости v_ij. Полная реакция F_ij отклонена на угол трения φ от нормали к соприкасающимся элементам пары и при любом положении точки касания К направлена по касательной к кругу трения радиуса ρ с центром в точке O_i (рис. 1.5). Этот круг называется кругом трения.

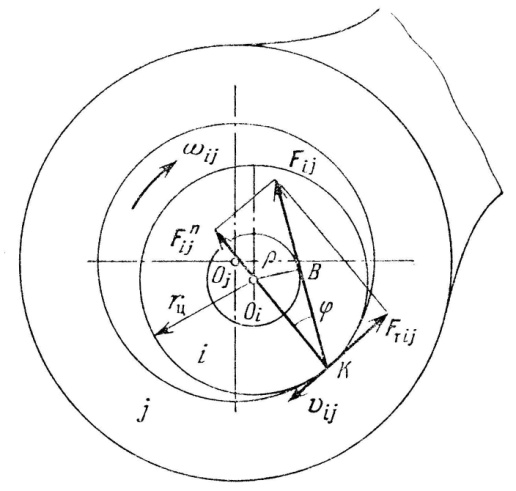
Рис. 1.5. Силы трения скольжения в цилиндрических кинематических парах

Из треугольника ВO_iК радиус круга трения

,

где r_ц – радиус цапфы, т.е. той части звена i, на которой расположены элементы вращательной пары.

При исследовании динамики шарнирных механизмов с учетом трения иногда удобнее считать полную реакцию F_ij проходящей через центр O_i. Тогда дополнительно надо учесть момент сил трения _тij, определяемый по условию

(1.22)

и направленный противоположно относительной угловой скорости _ij. Коэффициент трения в этой формуле должен определяться из экспериментальных данных для вращательной пары. Если же используются данные, полученные из опытов с плоскими поверхностями, то надо иметь в виду, что для трения цилиндрических поверхностей с внутренним касанием коэффициент трения получается больше, чем для плоских поверхностей.

В высших парах возможно взаимное качение звеньев. Сопротивление качению звеньев выражают моментом _тij, модуль которого определяется по формуле

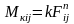, (1.23)

где k – коэффициент сопротивления качения, имеющий размерность длины (обычно см), – модуль результирующей силы нормальных давлений на поверхности трения. Направление момента _тij противоположно направлению относительной скорости, имеющей аналогичный индекс. Например, момент сил сопротивления качению _тij, действующих на звено i со стороны звена j, направлен противоположно угловой скорости _ij звена i по отношению к звену j.