
- •Механические колебания и виброакустическая защита транспортно-технологических строительных машин
- •«Наземные транспортно-технологические комплексы»
- •Введение
- •Характеристики сил в механизмах
- •1.1. Движущие силы
- •. Силы сопротивления
- •. Силы трения
- •. Силы упругости
- •. Импульсные и ударные силы
- •2. Уравнения движения механизмов
- •2.1. Число степеней свободы
- •2.2. Жесткость
- •2.3. Уравнения движения механической системы с одной степенью свободы.
- •2.4. Кинематика гармонического движения
- •2.5. Учет массы пружины
- •2.6. Вынужденные колебания
- •2.7. Резонанс
- •2.8. Кинематическое возбуждение
- •2.9. Инерционное возбуждение
- •2.10. Экспериментальное определение собственной частоты
- •2.11. Сложное (полигармоническое) возбуждение
- •2.12. Круговые колебания. Критическая частота вращения вала
- •2.13. Различные виды трения при колебаниях
- •3. Колебания системы с двумя степенями свободы
- •3.1. Собственные колебания
- •3.2. Вынужденные колебания
- •4. Вибрация и способы ее снижения
- •4.1. Общие сведения
- •4.2. Основные конструкционные особенности зтм.
- •4.3. Общая характеристика источников виброакустической энергии
- •4.4. Методы и средства снижения виброакустической энергии
- •5. Виброизоляция
- •5.1. Линейный виброизолятор
- •5.2. Виброизоляция при ударном воздействии
- •5.3. Виброизоляция при случайном воздействии
- •6. Динамическое гашение колебаний
- •6.1. Пружинный динамический гаситель
- •6.2. Динамический поглотитель колебаний
- •6.3. Динамический поглотитель колебаний крутильной системы
- •6.4. Ударные гасители колебаний
- •7. Уравновешивание механизмов и машин
- •7.1. Общие сведения об уравновешивании
- •7.2. Уравновешивание вращающегося тела
- •8. Вибропоглощение
- •8.1. Природа и характеристики потерь колебательной энергии в твердых телах
- •8.2. Расчет вибропоглощающих покрытий и конструкций
- •8.3. Конструкционные материалы с большими внутренними потерями
- •9. Характеристики вибрации, определяющие ее действие
- •9.1. Показатели интенсивности вибрации
- •9.2. Показатели спектрального состава вибрации
- •9.3. Допустимые значения уровней вибрации
- •Определение коэффициентов передачи при виброизоляции
- •9.5. Пассивная и активная виброизоляция сиденья самоходной машины
- •9.6. Виброизоляция автомобильных и тракторных двигателей
- •10. Теория и практика борьбы с шумом
- •10.1. Актуальность проблемы борьбы с шумом
- •10.2. Перспективы борьбы с шумом
- •10.3. Основные понятия и определения
- •10.4. Излучение и распространение звука
- •10.5. Распространение звука в помещении
- •10.6. Поглощение, отражение и прохождение звука
- •10.7. Интерференция звука
- •10.8. Дифракция звука
- •11.1. Характеристика шума
- •11.2. Спектральные и временные характеристики шума
- •11.3. Сложение шума двух и более источников
- •11.4. Перевод узд в уз
- •11.5. Вычитание уз (узд)
- •11.6. Расчет эквивалентного уз
- •11.7. Нормы шума на рабочих местах
- •11.8. Технические нормы шума машин
- •11.9. Нормирование ультразвука и инфразвука
- •12. Источники шума
- •12.1. Классификация
- •13. Механический шум
- •13.1. Зубчатые передачи
- •13.2. Подшипники
- •13.3. Роторы
- •13.4. Кулачковые механизмы
- •14. Аэродинамический шум
- •14.1. Шум струи
- •14.2. Шум вентиляторов
- •15. Гидродинамический шум
- •15.1. Источники шума
- •15.2. Шум гидронасосов
- •16. Электромагнитный шум
- •16.1. Электрические машины
- •16.2. Трансформаторы
- •17. Расчет звука в помещении от наружнего источника
- •17.1. Расчет структурного звука
- •17.2. Расчет эффективности звукоизолирующего капота
- •18. Характеристики шума в кабинах строительных
- •18.1. Характеристики внешнего шума
- •18.2. Снижение шума в кабинах. Методы и средства
- •18.3. Звукоизоляция и звукопоглощение
- •18.4. Виброизоляция и вибродемпфирование
- •18.5. Снижение внешнего шума
- •18.6. Глушители шума выпуска отработавших газов двигателей
- •Часть четвертая
- •19. Задачи и методы прогнозирования
- •19.1. Системный анализ
- •19.2. Математическая модель виброакустического процесса
- •19.3. Используемые конечные элементы
- •Формирование топологии и базы исходных данных
- •20.1. Топология и физико-геометрические характеристики элементов конструкции машины1
- •20.2. Аппроксимация конечными элементами колесного погрузчика
- •20.3. Сопоставление результатов численных исследований (мкэ)
- •20.4. Определение вклада воздушного и структурного шума
- •Виброакустические исследования дорожного
- •21.1. Топология дорожного снегоочистителя типа дэ-2101
- •Анализ результатов численных исследований мкэ виброакустического процесса на снегоочистителе
- •Первая часть:
- •Второй часть:
- •Третья часть:
- •Четвертая часть
- •Приложения
- •И их значений в м/с и м/с2 соответственно
- •Сведения об авторе
- •Механические колебания и виброакустическая защита транспортно-технологических строительных машин
Характеристики сил в механизмах
1.1. Движущие силы
Характеристика силы1. При решении большинства задач динамики механизмов надо знать определяющее действие одного тела на другое. Силы, действующие на звенья (твердые тела) механизма, могут быть функциями времени. Например, движущая сила, действующая на лопасть гидравлической муфты, зависит от времени истечения жидкости через постоянное отверстие. Чаще, однако, переменные силы, действующие на звенья механизма, связаны или с перемещениями, или со скоростями точек приложения этих сил. Например, сила пружины связана с ее деформацией, т.е. с перемещением точки приложения силы; сила взаимодействия проводника с током и магнитного поля в электродвигателе связана со скоростью движения проводника относительно поля и т.д.
Функциональная зависимость, связывающая модуль силы и кинематические параметры (время, координаты и скорость точки приложения силы), называется характеристикой силы. Модуль силы в этой зависимости может быть и функцией, и аргументом. Однако для удобства расчетов будем всегда считать, что модуль силы есть функция указанных кинематических параметров.
Силы движущие и силы сопротивления. Движущей силой называется сила, элементарная работа которой на возможном перемещении точки ее приложения положительна. Силой сопротивления называется сила, элементарная работа которой на возможном перемещении точки ее приложения отрицательна.
Входные и выходные звенья. Входным звеном механизма называется звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Выходным звеном называется звено, совершающее движение, для которого предназначен механизм. Движущие силы в механизме действуют обычно на входные звенья, а силы сопротивления – на выходные звенья.
Ведущие и ведомые звенья. Ведущим (иначе – движущим) звеном называется звено, для которого элементарная работа внешних сил, приложенных к нему, является положительной2. Ведомым звеном называется звено, для которого элементарная работа внешних сил, приложенных к нему, является отрицательной или равна нулю. Одно и то же выходное звено на отдельных участках движения может быть то ведомым, то ведущим. Аналогично входное звено, которое по признаку действия сил обычно является ведущим, на некоторых участках движения может быть ведомым.
. Силы сопротивления
Характеристики сил сопротивления в машинах определяются условиями, зависящими от того процесса, для выполнения которого предназначена машина. Эти силы действуют на выходные силы механизма и могут быть функциями перемещений, скоростей и времени. Для многих машин общим свойством этих характеристик является их периодичность во времени. Внутри каждого периода нелинейные характеристики сил сопротивления представляются приближенными выражениями, получаемыми из разложения в ряды Фурье. Если ограничиться k+1 членами этого разложения, то характеристику силы сопротивления Fc(t) внутри периода времени продолжительностью Т можно приближенно представить в виде
 ,
(1.1)
,
(1.1)
где
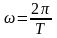 ,
(1.2)
,
(1.2)
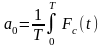 ,
(1.3)
,
(1.3)

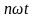
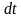 ,
(1.4)
,
(1.4)
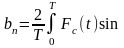 .
(1.5)
.
(1.5)
Аналогичные формулы получаются, если считать силу Fc функцией перемещения х.
Выражение в скобках, стоящее под знаком суммирования в формуле (1.1), называется гармоникой порядка n. Следует обратить внимание на то, что в характеристиках сил сопротивления, действующих на звенья механизма, не обязательно первая гармоника имеет наибольшее значение по сравнению с другими. Гармоника, которая имеет максимальное значение (по модулю), называется доминирующей или доминантой. Коэффициенты а0, an и bn каждой гармоники находятся по формулам (1.3) – (1.5), если известно аналитическое или графическое представление характеристики Fc(t) с использованием метода гармонического анализа. Заметим также, что коэффициенты a0, an и bn не зависят от переменной t. По свойству определенных интегралов их значения зависят только от пределов интегрирования и вида функции Fc(t). На этом основании переменную интегрирования в формулах (1.3) – (1.5) иногда обозначают другой буквой, чтобы подчеркнуть независимость коэффициентов a0, an и bn от текущих значений переменной t.
Если сила Fc(t) не является периодической функцией, то формула (1.1) используется для приближенного выражения характеристики силы только на заданном участке 0 ≤ t ≤ l, полагая T = l, или же используются понятия интеграла Фурье и спектральной плотности.
Интеграл Фурье. Для непериодической функции f(t), удовлетворяющей условию абсолютной интегрируемости на всей числовой оси, т.е. условию сходимости интеграла
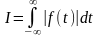 ,
,
предельный переход от ряда Фурье при T→∞ дает выражение f(t) в интегральной форме:
f(t)
=
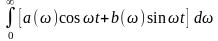 ,
(1.6)
,
(1.6)
где
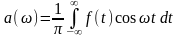 ,
(1.7)
,
(1.7)
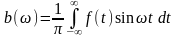 ,
(1.8)
,
(1.8)
или, после тригонометрических преобразований,
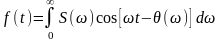 ,
(1.9)
,
(1.9)
где
 ,
(1.10)
,
(1.10)
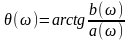 .
(1.11)
.
(1.11)
На рис. 1.1 показано графическое изображение соотношения между формулами (1.6) – (1.9). Для фиксированного значения ω отрезок ОК дает S(ω) в формуле (1.9), а проекция его на направление, образующее с осью абсцисс угол ωt, дает отрезок ОА = S(ω,t), равный значению подынтегральной функции в формулах (1.6) – (1.9), что и доказывает их тождественность.
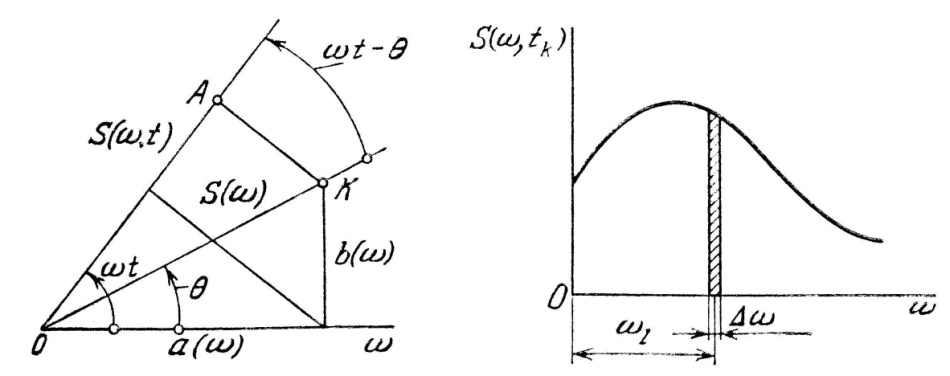
Рис. 1.1. Графическое изображение соотношения между формулами (1.6) и (1.9)
Рис. 1.2. График изменения подынтегральной функции от угловой частоты (ω)
В отличие от ряда Фурье, в котором угловые части гармонических составляющих (гармоник) ω, 2ω, …, nω, … образуют дискретный спектр, интеграл Фурье характеризуется непрерывным спектром ω от 0 до ∞, причем для каждого значения t интеграл Фурье дает значение функции f(t) в виде «суммы» гармоник с непрерывно изменяющейся угловой частотой ω и амплитудой S(ω).
Для четных функций f(-t) = f(t) ряд Фурье содержит лишь слагаемые с коэффициентом an (разложение по косинусам), для нечетных функций f(-t) = - f(t) – слагаемые с коэффициентами bn (разложение по синусам). Соответственно интеграл Фурье для четных функций имеет вид
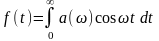 .
(1.12)
.
(1.12)
Вследствие четности функции f(t) коэффициент a(ω) достаточно вычислить в пределах от 0 до ∞ и затем удвоить:
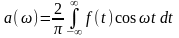 .
(1.13)
.
(1.13)
Для нечетных функций интеграл Фурье
 ,
(1.14)
,
(1.14)
где
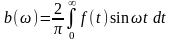 .
(1.15)
.
(1.15)
Спектральная плотность. На рис. 1.2 для фиксированного значения t = tk показан график изменения подынтегральной функции интеграла Фурье S(ω, tk) в зависимости от угловой частоты ω. Площадь, заключенная между этим графиком и осью абсцисс, дает согласно (1.6) значение функции f(t) при t = tk. Выделим из этой площади элементарную площадку шириной ∆ω вблизи текущего значения ω = ωl. Тогда средняя ордината графика S(ω, tk) дает среднюю плотность распределения функции f(tk) по оси абсцисс на участке ∆ω вблизи ω = ωl. При ∆ω → 0 получаем, что функция S(ω, tk) дает плотность распределения функции f(t) по частоте ω при значении t = tk. Плотность распределения функции f(t) по частоте ω независимо от текущего значения переменной t, называется спектральной плотностью S(ω) и определяется по (1.10).
Для четных функций b(ω) = 0 и тогда
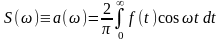 .
(1.16)
.
(1.16)
В зависимости от физического смысла функции f(t) спектральная плотность S(ω) получает соответствующее название. Например, если f(t) = Fc(t), то S(ω) называют спектральной плотностью силы сопротивления, зависящей от времени; если потенциальная энергия системы пропорциональна f(t) = x2(t), где x – обобщенная координата системы, то S(ω) называют спектральной плотностью энергии и т.д.
