19.2. Математическая модель виброакустического процесса

Среди современных методов численного анализа быстропеременных процессов методу конечных элементов (МКЭ) принадлежит особое место. Благодаря своим, достаточно простым математическим моделям и очевидному физическому представлению, МКЭ является наиболее эффективным методом решения различных задач механики сплошной среды. Эффективность метода и его распространение объясняются также наличием большого числа общих программ для ЭВМ с высокой степенью автоматизации генерирования сети конечных элементов, формирования и решения огромного числа алгебраических уравнений, а также хорошей численной и графической интерпретацией полученных результатов.

Анализ и решение проблемы прогнозирования виброакустических параметров ЗТМ как сложных динамических систем сводится к пошаговому процессу. Процесс представляется простым алгоритмом, включающим шесть важнейших операций: дискретизацию сплошной среды; выбор интерполяционных функций; вычисление характеристик элементов конструкций; формирование уравнений для ансамбля конечных элементов; решение системы уравнений; расчет требуемых параметров.

Численные исследования быстропеременных процессов на ЗТМ выполнялись по программному комплексу ИМПУЛЬС, который ориентирован на проведение динамических расчетов стержневых и плитных пространственных конструкций при импульсном, гармоническом и других характерах внешних возбуждающих воздействий.

В основе численных алгоритмов, реализованных в комплексе, лежит МКЭ в форме метода перемещений. Расчетная схема в этом случае представляется по МКЭ в виде ансамбля конечных элементов (КЭ), соединённых друг с другом в узлах.

Уравнение равновесия i-го КЭ записывается в локальной системе координат (ЛСК) элемента и в матричной форме имеет вид

, (19.1)

где , , – матрицы масс, демпфирования и жесткости i-го КЭ в ЛСК; , –векторы перемещений и внешних сил, действующих на i-й элемент со стороны других КЭ.

Размерности матриц и векторов в (19.1) определяются количеством степеней свободы (СС) элемента, в качестве которых принимаются независимые перемещения узлов КЭ.

Переход от ЛСК i-го элемента к глобальной системе координат (ГСК) для всей конструкции осуществляется с помощью соотношений

; ; , (19.2)

где – блочно-диагональная матрица преобразования координат, имеющая раздельные блоки по узлам КЭ и видам СС (линейные и угловые); – j-й блок матрицы преобразования, составленный из направляющих косинусов осей i-й ЛСК в ГСК; , - векторы i-го элемента в ГСК.

Умножая слева (19.1) на и подставляя (19.2), получим уравнение равновесия i-го КЭ в ГСК

, (19.3)

где и соответственно , – матрицы элемента в ГСК. Уравнения равновесия k-го узла расчетной схемы записываются в ГСК в аналогичном виде:

, (19.4)

где , , 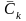– диагональные матрицы, учитывающие инертные свойства k-го узла, опорные демпферы и упругие связи; 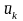, , – векторы перемещений, внешней узловой нагрузки и реакций в абсолютно жестких опорных связях узла.

В данном случае суммирование сил ведётся по элементам, примыкающим к k-му узлу.

Динамическое уравнение (математическая модель) равновесия всего ансамбля элементов и узлов получается путём суммирования (19.3) по КЭ и (19.4) по узлам, причём силы сокращаются, т.к. являются внутренними для расчетной схемы конструкции:

, (19.5)

здесь и аналогично , – глобальные матрицы ансамбля; , , – глобальные векторы, соответствующие произвольному моменту времени t. Степени свободы, соответствующие абсолютно жестким опорным связям, обычно исключают из системы уравнений, поэтому вектор реакций в дальнейшем не учитывается.

Интегрирование матричного уравнения (19.5) по времени выполняется прямым пошаговым методом Ньюмарка, который описывается на разных временных соотношениях между векторами в моменты t и t + :

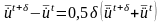, (19.6)

где  – шаг интегрирования.

С помощью соотношений (19.6) дифференциальное уравнение (19.5) преобразуется в алгебраическое уравнение

, (19.7)

где разрешающая матрица и вычисляемый на каждом временном шаге вектор правой части определяются выражениями

; (19.8)

. (19.9)

Таким образом, по методу Ньюмарка на каждом временном шаге выполняются следующие операции:

1) вычисление по (19.9);

2) нахождение из решения системы (19.7);

3) определение и из соотношений (19.6). С целью повышения эффективности алгоритма решение системы уравнений (19.7) осуществляется итерационным методом. Итерационный процесс решения системы выполняется в следующей последовательности:

1. вычисление поправки :

; (19.10)

2. определение следующего приближения к решению :

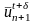; (19.11)

3. коррекция невязки :

, (19.12)

здесь n=0,1,2,... – номер итерации; – итерационный параметр Чебышева; –итерационная блочно-диагональная матрица, составляемая из легко обращаемых диагональных блоков матрицы .

Глобальная матрица демпфирования в уравнении (19.3) представляется в соответствии с гипотезой вязкого сопротивления Фойгта:

, (19.13)

где , – матрицы масс и жесткости i-го КЭ; , – коэффициенты внешнего и внутреннего вязкого сопротивления. Здесь символ обозначает суммирование матриц отрицательных элементов по правилам МКЭ формирования глобальной матрицы.

Гипотеза Фойгта проста, удобна в реализации и позволяет качественно описать процесс рассеивания виброакустической энергии в конструкции. Однако она является частотно зависимой, что не подтверждается экспериментальными данными для большинства материалов и не может служить для количественной оценки диссипации виброакустической энергии в широком диапазоне частот. Тем не менее, данную гипотезу вполне корректно можно использовать в случае описания быстропеременных процессов с узким диапазоном частот, т.е. для виброакустического расчета вынужденных колебаний системы под воздействием периодической возмущающей силы. При этом коэффициент внутреннего вязкого сопротивления определяется по формуле

, (19.14)

где Т – период возмущающей силы;  – коэффициент потерь, который принимается независящим от частоты колебаний.

В случае численных исследований звуковой вибрации конструкций машины внешнее вязкое сопротивление воздушной среды не учитывалось, а коэффициенты потерь  принимались равными: 0,0001 – для всех стальных элементов; 0,14 – для элементов, моделирующих шины, грунт, гидроцилиндры; 0,10 – для виброизоляторов.