2.4. Кинематика гармонического движения

Рассмотрим подробнее характер движения колеблющейся массы А (рис. 2.1, а). Путь, совершаемый за одно полное колебание, т.е. О₁ОО₂ + О₂ОО₁, изображается в зависимости от времени синусоидой, так как

.

Построение кривой x = f(t) показано на рис. 2.5. Максимальное отклонение равно ОО₁ или х₀.

Опишем радиусом, равным х₀, окружность. Колеблющаяся точка, изображающая массу А, в момент начала отсчета времени (t = 0) находилась в точке А₁. Движение точки А₁ на пути А₁ОА₂О₁ + О₁О₂ + О₂А₁, т.е. полное колебание, можно представить себе как движение проекции конца радиуса х₀, вращающегося с угловой скоростью ω. В самом деле, за время t₁, протекшее от t = 0, радиус пройдет угол ωt₁ = ε, а к моменту t пройдет угол ωt. Пусть x проекции конца радиуса от среднего положения О изображается отрезком ОА₂:

,

что совпадает с уравнением (2.6). Величину х₀ называют амплитудой колебания. Синусоида, изображающая зависимость пути от времени, на рис. 2.5 построена в масштабе х₀ = 1. Длина окружности (r = OO₁ = х₀ = 1) равна 2π или, выраженная через ω и время, равна ωТ, где Т – время, за которое радиус ОО₁ совершает один полный оборот, а его проекция А проходит путь ОО₁О₂О, т.е. совершает одно полное колебание.

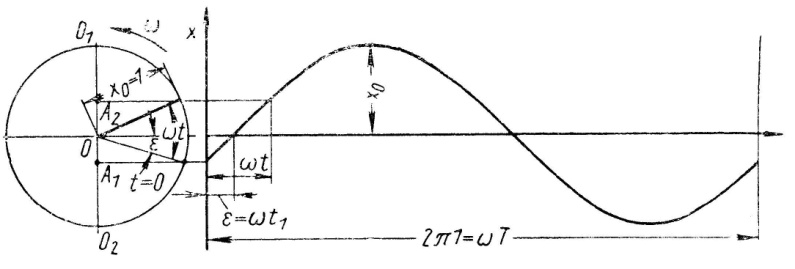
Рис. 2.5. Синусоидальная зависимость пути от времени

Это время называют периодом колебания. Угол ωt₁, соответствующий начальному значению отклонения точки от среднего положения в момент t = 0, называют фазовым углов (начальной фазой колебания). Если начинать отсчет времени в момент, когда х = 0, то и фазовый угол ε = ωt₁ тоже равен нулю.

Следовательно, угловая скорость вращения радиуса ОО₁, называемая круговой частотой, связана с периодом колебания (временем, за которое совершается одно полное колебание) зависимостью 2π = ωТ, откуда период Т = . Частотой колебаний f называют число колебаний в 1 сек:

или

. (2.16, а)

Если, как это часто делается, указывать частоту в виде числа колебаний в минуту n, то

. (2.16, б)

Так как собственная частота колебаний f или собственное число в минуту n связаны с ω выражениями (2.16, а) и (2.16, б), а ω не зависит от амплитуды колебаний х₀, то и частота (или число собственных колебаний в минуту) при гармонических колебаниях не зависит от амплитуды: она остается постоянной, и при больших и при малых амплитудах.

Собственная частота колебаний системы представляет собой ее важнейшую вибрационную характеристику. Определение собственной частоты системы – почти всегда первая цель исследования колебаний.

Нужно подчеркнуть, что фазовый угол только мера времени и ничего пространственного в колебаниях ему не соответствует.

Точно так же вращение радиуса х₀ со скоростью ω только способ изображения гармонического движения колеблющейся прямолинейно точки А на пути О₁О₂ (рис. 2.5).

Синусоида пути точки, совершающей гармонические колебания, показана на рис. 2.6, а; для простоты чертежа фазовый угол принят равным нулю. Скорость и ускорение гармонического колебания показаны на рис. 2.6, б и в.

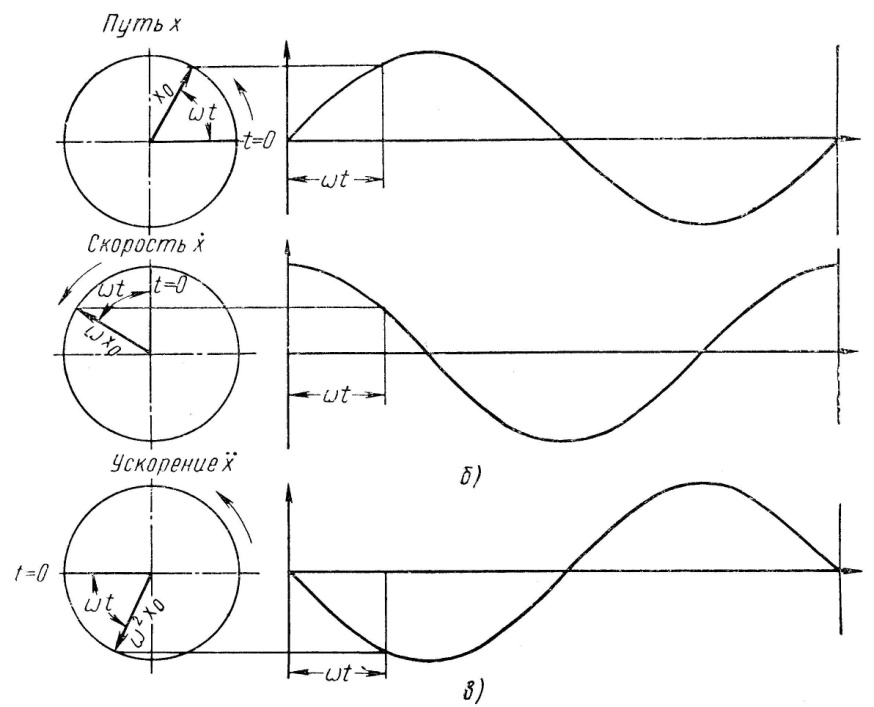
а)

б)

в)

Рис. 2.6. Кинематика гармонического колебания

Дифференцируя х = х₀ sin ωt, находим скорость

(2.17)

и, дифференцируя ещё раз, определяем ускорение

.

Если вместо х₀sin ωt в последнее выражение подставить х, то найдем:

. (2.18)

Следовательно, в гармоническом колебании ускорение движения пропорционально отклонению колеблющегося тела от среднего положения (когда пружина не сжата и не растянута) и направлено в противоположную сторону.

В уравнении движения (2.8), из решения которого вытекает равенство (2.18), восстанавливающая сила, вызывающая движение, пропорциональна отклонению х (равна сх), или деформации пружины. Так как мера этой силы , то очевидно, что и ускорение должно быть пропорционально х. Итак, гармоническим, удовлетворяющим условию (2.18), колебание оказывается потому, что сила упругости пружины пропорциональна деформации, т.е. простая пружина (см. рис. 2.1, а) сделана из стали, подчиняющейся закону Гука.

Если бы колебания происходили под действием комбинации пружин, показанной на рис. 2.4, а, или резинового элемента, то сила упругости не была бы пропорциональна перемещению и условие (2.18) не выполнялось бы (нелинейные колебания).