3. Колебания системы с двумя степенями свободы

3.1. Собственные колебания

В некоторых случаях частоту свободных колебаний системы с двумя степенями свободы можно определить, пользуясь уже известным решением для системы с одной степенью свободы. На рис. 3.1, а показана крутильная система, состоящая из вала с жесткостью с и двух дисков J₁ и J₂. Если закрутить вал, как показано стрелками, и отпустить диски, то форма собственных колебаний изобразится прямой линией BD (моментом инерции вала пренебрегаем).

Рис. 3.1. Системы с двумя массами

Сечение х неподвижно, его амплитуда равна нулю. Точка х называется узлом колебаний. Найдем частоту собственных колебаний ω_с и форму колебаний, т.е. отношение амплитуд , рассматривая систему как состоящую из двух систем с одной массой каждая, закрепленных в узле х. Ясно, что узел должен расположиться так, чтобы частота колебаний левой и правой частей (l₁ и l₂) были одинаковы, так как вал должен колебаться с единой частотой всей системы.

Следовательно,

;

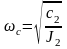
или

; .

Нужно выразить известные нам жесткости с₁ и с₂ через известную жесткость вала с.

Если закрутить вал моментом М, то (рис. 3.2, а) М = сφ; М = с₁φ₁ и М = с₂φ₂, откуда , и . И так как φ₁ + φ₂ = φ, то , или .

Если взять n последовательно включенных пружин или отрезков вала, то

. (3.1)

Рис. 3.2. Сложение крутильных жесткостей

При параллельном расположении пружин или валов, как на рис. 3.2, б, суммарная жесткость:

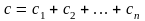. (3.2)

В самом деле, на рис. 3.2, б видно, что угол закрутки обоих концентрически расположенных валов одинаков, φ, а момент М передается частично через один вал (М₁) и частично через другой (М₂). Следовательно, М = с₁φ, М = с₂φ, и так как М = М₁ + М₂, то сφ = с₁φ + с₂φ, или с = с₁ + с₂.

Сложим жесткости с₁ и с₂ по формуле (3.1):

,

откуда

;

. (3.3)

Для системы из двух масс на рис. 3.1, б

.

Из подобия треугольников ABx и CDx (рис. 3.1, а) вытекает, что , так как податливости пропорциональны длинам отрезка вала. Следовательно, форма колебаний определяется отношением моментов инерции дисков.

Частотное уравнение. Классический путь определения собственных частот системы с двумя массами (т.е. с двумя степенями свободы, так как движение системы можно задать двумя углами отклонения от среднего положения: φ₁ для диска J₁ и φ₂ для диска J₂) состоит в решении уравнений движения. Для каждой из масс системы (см. рис. 3.1, а) напишем свое уравнение. Момент сил упругости, действующий на диск J₁, равен с(φ₁ - φ₂).

На диск J₂ действует такой же по величине момент, но с обратным знаком, так как, считая углы поворота дисков положительными в направлении вращения часовой стрелки (если смотреть по стрелке Б), найдем, что при φ₁ > φ₂ момент сил упругости стремится повернуть диск J₁ против часовой стрелки, а диски J₂ – по часовой стрелке. Следовательно, уравнения движения будут

(3.4)

Решение ищем в форме φ₁ = φ₁₀ sinωt и φ₂ = φ₂₀ sinωt. После подстановки и φ в уравнение (3.4) получим (индекс «0» опускаем)

(3.5)

Отметим, что здесь неизвестны частота ω и амплитуды φ₁ и φ₂, а уравнений только два. Так как амплитуды при свободных колебаниях зависят от произвольного начального угла закрутки (рассматриваются колебания без потерь), то нужно знать не φ₁ и φ₂, а только форму колебаний, т.е. отношение и собственную частоту ω. Для этого достаточно двух уравнений (3.5).

Углы φ₁ и φ₂ будут иметь отличные от нуля значения, если определитель, составленный из коэффициентов при φ₁ и φ₂, равен нулю, т.е. если

. (3.6)

Развертывая этот определитель, находим

или (3.7)

.

Уравнение (3.7) называют частотным. Решая его, получаем два решения:

,

. (3.8)

Решение ω_с = 0 относится к тому случаю, когда движение обоих дисков происходит в одну сторону, т.е. крутильных колебаний нет. Решение (3.8) совпадает с полученным ранее решением (3.3). Если подставить 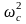в уравнения (3.5), то из них находим одно и то же решение:

, (3.9)

т.е. форму колебаний. Собственная частота, как и для системы рис. 2.1, а, не зависит от амплитуд колебаний; ей соответствует определенная, собственная форма колебаний.

Отыскание собственной частоты колебаний такой простой системы, как на рис. 3.1, а или 3.1, б, классическим методом не сложно.

Однако с увеличением числа масс (числа степеней свободы) частотное уравнение становится громоздким. Приходится либо отказаться от него и применить другие методы, либо прибегнуть к помощи электронной цифровой вычислительной машины, для которой решение системы уравнений со многими неизвестными (определение формы) или высокой степени (определение собственной частоты) представляет собой простую операцию; для нее разработаны стандартные программы.

Колебания тела на двух пружинах. Двумя степенями свободы обладает и тело (жесткая балка на двух пружинах, рис. 3.3, а). Хотя здесь колеблется только одна масса, но описание ее движения требует двух независимых координат, например х и φ. Пусть систему вывели из состояния покоя, нажав на один конец балки. Тогда одновременно возбудятся и колебания вверх и вниз, и покачивание вокруг оси, перпендикулярной чертежу и проходящей через цент тяжести.

Пусть пружины имеют одинаковую жесткость, центр тяжести балки расположен посередине между осями пружин (простейшая задача). Если масса балки m, а ее момент инерции при повороте вокруг центра тяжести J, то получим два следующих дифференциальных уравнения движения:

(3.10)

а)

б)

в)

г)

Рис. 3.3. Вынужденные колебания систем с двумя степенями свободы

Знаки в левых частях определяются тем, что обе силы упругости при линейном перемещении направлены против отклонения х, а моменты сил упругости при повороте направлены справа против положительного отклонения (пружина сжимается), а слева – в сторону отклонения (сжатая пружина распрямляется). Из системы уравнений (3.10), полагая х = х₀ sin ωt и φ = φ₀ sin ωt, находим

(3.11)

Каждое из уравнений (3.11) решается независимо от другого, и мы получаем две собственные частоты

и .

Независимость уравнений физически объясняется тем, что вследствие полной симметрии системы относительно центра тяжести можно было бы возбудить чисто прямолинейные колебания, сместив центр тяжести вниз, так, чтобы обе пружины сжались на одинаковую величину, или только вращательные колебания (угловые повороты), если удержать середину балки на начальном уровне и нажать на один из концов. Конечно, идеальная симметрия, т.е. полное равенство жесткостей с и точное расположение центра тяжести посередине балки, в действительности неосуществимы, но практически тот или иной из двух видов колебаний будет преобладать при описанных способах начального возбуждения. Однако если частоты ω_с1 и ω_с2 близки между собой, то колебания могут быть сначала, допустим, прямолинейными, даже чисто вращательными. Запас потенциальной энергии пружин при этом делится по-разному, между двумя видами колебаний в разные отрезки времени колебательного процесса.