2.5. Учет массы пружины

В начале этой главы собственная частота колеблющейся системы вычислялась из условия постоянства запаса энергии. Вместо интегрирования уравнения (2.3) можно приравнять максимальное значение кинетической энергии начальному запасу потенциальной. Из такого уравнения нельзя будет найти закон движения, но можно определить собственную частоту колебаний. Закон же движения (т.е. синусоидальность колебаний) можно теперь считать известным, если только характеристика пружины прямолинейна (см. рис. 2.1, а).

Для системы, показанной на рис. 2.1, а, можно написать или, при гармоническом колебании, , откуда , как было найдено ранее.

Этот простой способ позволяет учитывать влияние массы пружины на частоту колебаний. Рассмотрим, например, как изменится выражение частоты для пружины с грузом на конце, если учитывать массу пружины.

Потенциальная энергия растянутой на х₀ пружины, очевидно, останется прежней, т.е. будет равна 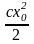. Для вычисления кинетической энергии рассмотрим элемент пружины длиной dl (рис. 2.9), массу которого обозначим через μdl (μ – масса участка пружины длиной в 1 см). Следовательно, кинетическая энергия элемента с массой μdl при проходе через среднее положение равна , а кинетическая энергия всей массы пружины (m_пр)

,

так как m_пр = μL. Максимальная кинетическая энергия массы А равна , откуда полная максимальная кинетическая энергия

. (2.19)

Рис. 2.9. Расчетная схема учета массы пружины

Приравнивая к потенциальной энергии W₀, получим уравнение

, (2.20)

откуда

. (2.21)

Рассуждая аналогично, устанавливаем влияние момента инерции закручиваемого вала (см. рис. 2.1, б):

,

где J_в – момент инерции вала.

Вывод влияния массы балки на частоту колебаний груза на ней несколько сложнее, так как потенциальная и кинетическая энергии элементов такой системы зависят от формы упругой линии изогнутой балки. Здесь отметим только, что приближенное решение для случая, показанного на рис. 2.1, в, имеет вид

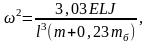
где m_б – масса балки.

2.6. Вынужденные колебания

Рассмотрим движения системы (рис. 2.1, а), когда к массе приложена периодическая сила, действующая вдоль оси пружины и изменяющаяся во времени по закону синуса, т.е. гармоническая возбуждающая сила. Конечно, практически очень часто периодическая возбуждающая сила бывает не гармонической и изменение ее во времени происходит по какой-нибудь сложной кривой. Но удобно начать изучение вынужденных колебаний под действием гармонической возбуждающей силы, так как для этого простого случая легко найти закон движения. Из чисто физических представлений нетрудно вывести основную характеристику движения: ясно, что частота вынужденных колебаний будет равна частоте возбуждающей силы, так как, естественно, когда сила меняет свое направление, будет меняться и направление движения.

Теперь на массу А действуют две силы: возбуждающая сила P sin ωt, где ω – круговая частота (угловая скорость радиуса на диаграмме рис. 2.5, где синусоида изображает закон изменения силы за период Т), и сила упругости – сх. Сопротивлениями пока по-прежнему пренебрегаем. Сумма этих сил определяет движение массы m. По второму закону Ньютона она измеряется произведением ; следовательно,

или

. (2.22)

Уравнение (2.22) неоднородное, т.е. правая его часть, в отличие от однородного уравнения (2.8), не равна нулю.

Из теории дифференциальных уравнений известно, что общее решение неоднородного уравнения (2.22) равно сумме общего решения однородного уравнения (2.8) и частного решения, удовлетворяющего уравнению (2.22). Чтобы найти такое частное решение, зададимся пробным решением x = x₀ sin ωt, т.е. примем, что гармоническая сила с частотой ω¹ создает гармоническое движение с той же частотой, и попробуем подобрать x₀ так, чтобы пробное частное решение удовлетворило уравнению (2.22).

Дифференцируя дважды x = x₀ sin ωt, найдем, что . Подставляя выражения для и х в уравнение (2.22), получим

или

. (2.23)

Решая уравнение (2.23) относительно x₀, видим, что ему удовлетворяет значение

. (2.24)

При значении x₀, определяемом выражением (2.24), пробное решение будет, следовательно, удовлетворять уравнению (2.22), в чем легко убедиться подстановкой в него х и при .

Итак, общее решение уравнения (2.22) будет иметь следующий вид:

; (2.25)

здесь ω_с – собственная частота (свободных) колебаний системы, чтобы отличить эту постоянную характеристику системы с, m (см. рис. 2.1, а) от частоты возбуждающей силы ω, которая не зависит от массы и упругости системы и может быть задана как угодно.

Первые два члена в правой части уравнения (2.25) выражают собственные колебания системы [см. уравнение (2.10)], где нужно только ввести новое обозначение ω_с вместо ω. В действительных условиях на колеблющуюся массу всегда действуют сопротивления: трение массы А о плоскость В, сопротивление воздуха, внутреннее трение в материале испытывающей деформации пружины или резины.

Если начальные условия движения таковы, что возникнут собственные колебания (например, сила P ≠ 0 в момент приложения к покоящейся массе), то запас энергии собственных колебаний W₀ постепенно израсходуется на преодоление сопротивлений и собственные колебания массы А затухнут. Практический интерес представляют поэтому установившиеся вынужденные колебания (когда собственные колебания уже затухнут), т.е. третий член уравнения (2.25):

. (2.26)

Уравнение (2.26) выражает закон движения массы при установившихся вынужденных колебаниях. Максимальное отклонение (амплитуда вынужденных колебаний):

; (2.27)

здесь 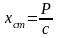– прогиб упругого элемента жесткостью с, если к ней приложить статически постоянную нагрузку Р, равную амплитуде возбуждающей силы P sin ωt; ω_с = – собственная частота системы.

Множитель обозначим через К и запишем амплитуду вынужденных колебаний (2.27) в виде

.

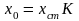Величину К называют коэффициентом усиления (или динамическим коэффициентом). График изменения коэффициента усиления (или, в другом масштабе, амплитуды x₀) показан на рис. 2.10 в зависимости от отношения частоты возбуждающей силы к собственной частоте колебания системы . Амплитуда вынужденных колебаний только при очень медленных колебаниях (ω ‹‹ ω_c) равна практически статическому прогибу под действием силы Р. По мере приближения ω к ω_c амплитуды возрастают, т.е. динамические прогибы при колебаниях усиливаются, становятся во много раз больше статических, поэтому величина К названа коэффициентом усиления.