2.8. Кинематическое возбуждение

Когда возбуждающий момент приложен к диску на закрепленном вале и имеет частоту, близкую к собственной частоте системы, то он вызывает большие колебания диска. Рассмотрим, какое действие окажет такое же по частоте возбуждение, если оно приложено к свободному концу вала; на другом конце сидит диск (рис. 2.13, а).

Обозначим амплитуду гармонического движения на конце вала 1 через φ₀₁, а отклонение в плоскости диска – через φ₂. Деформация вала:

.

Этой деформации соответствует момент сил упругости с (φ₂ - φ₀₁ sin ωt), вызывающий движение диска, и уравнение движения будет иметь следующий вид:

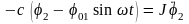. (2.29)

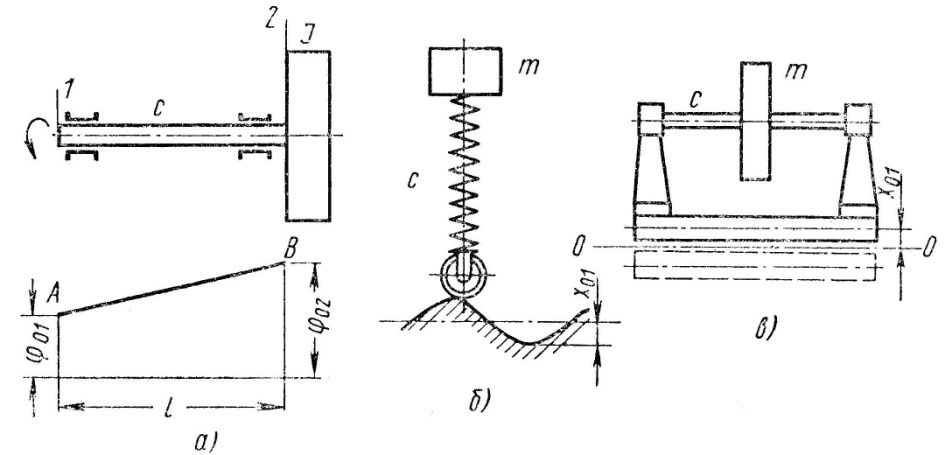
Рис. 2.13. Кинематическое возбуждение

Беря частное решение в виде φ₂ = φ₀₂ sin ωt, т.е. полагая, что гармоническое движение конца вала 1 создает тоже гармоническое колебания диска в плоскости 2, найдем то значение амплитуды диска φ₀₂, при котором удовлетворяется уравнение (2.29). После двукратного дифференцирования выражения для φ₂ и подcтановки 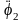и φ₂ в уравнение (2.29) получим, разделив все члены на sin ωt,

или

, (2.30)

где , т.е. собственная частота системы, если вал закреплен в точке 1.

Следовательно, кинематическое возбуждение системы гармоническим движением свободного конца вала создает амплитуду с тем же коэффициентом усиления, что и гармонический момент, приложенный к диску, но вместо статического отклонения х_ст в формуле (2.27) и в уравнении (2.30) стоит φ₀₁ – амплитуда возбуждаемого конца вала.

При очень медленном движении, когда ω → 0, φ₀₂ = φ₀₁, т.е. вал движется как одно целое и амплитуда диска та же, что и свободного конца вала. То же было бы и при абсолютно жестком вале, т.е. когда с = ∞ и ω_с = ∞. В этом случае вал с диском – твердое тело, и амплитуды всех его сочетаний одинаковы. В действительных условиях возникает форма вынужденных колебаний, показанная на рис. 2.13, а, где на перпендикулярах к отрезку, изображающему длину вала, отложены амплитуды колебаний концов φ₀₁ и φ₀₂. Наклон прямой АВ характеризует напряженность вала, так как деформация единицы длины вала равна .

Схема кинематического возбуждения гармонических линейных колебаний показана на рис. 2.13, б. Таков, например, характер возбуждения колебаний кузова, когда колесо подрессоренного автомобиля наезжает на неровность, имеющую форму синусоиды. Это равносильно перемещению конца пружины по гармоническому закону при неподвижной оси пружины.

Кинематическое возбуждение массы ротора m на валу с движением фундаментальной плиты, которой передаются внешние колебания (например, от соседней машины) через грунт, изображено на рис. 2.13, в. Для случаев, показанных на рис. 2.13, б и в, очевидно справедлива формула (2.30), где вместо амплитуды колебаний конца вала φ₀₁ нужно подставить максимальное линейное перемещение колеса или плиты х_01.

2.9. Инерционное возбуждение

Очень часто колебания создаются силами инерции или, точнее, движением в соответствии с законом центра инерции. Чтобы хорошо представить себе, как это происходит, рассмотрим сначала несколько идеализированный случай, показанный на рис. 2.14.

Пусть поршневой двигатель работает не закрепленным болтами на идеально гладком фундаменте, по которому фундаментальная плита двигателя может скользить без трения. Газы через поршень, шатун и шейки вала давят на рамные подшипники, стремясь сдвинуть весь двигатель вправо. В то же время газы давят на крышку цилиндра и через нее на раму, стремясь сдвинуть весь двигатель влево. Эти внутренние силы уравновешиваются, а других сил, т.е. внешних, нет. Но при перемещении поршня, например, влево расположение масс в двигателе изменяется, а центр тяжести, как известно из механики, при отсутствии внешних сил должен остаться неподвижным, т.е. весь двигатель должен передвинуться вправо.

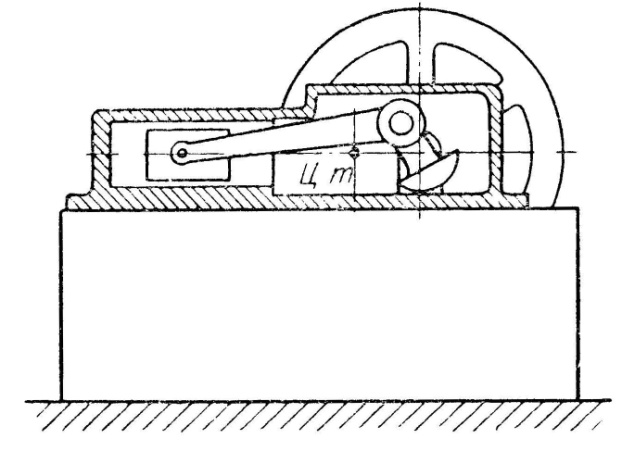
Рис. 2.14. Инерционное возбуждение

Следовало бы говорить не о центре тяжести, а о центре инерции, но если представить все связанные между собой части (цилиндр, станина, поршень, шатуны, вал) как единое тело, то центр тяжести такого тела и центр инерции совпадают. При этом, чтобы центр тяжести системы остался неподвижным, тяжелые массы двигателя должны сместиться незначительно, несмотря на большой ход сравнительно легкого поршня. Если, например, поршень и движущаяся поступательно часть шатуна весят 15 кг (пусть колено вала уравновешено противовесом, тогда вращение вала не изменяет положения центра тяжести), а двигатель весит 2400 кг, то при ходе поршня в 320 мм двигатель должен весь передвинуться на фундаменте на , т.е. на 2 мм (из одного крайнего положения в другое). При работе двигателя он будет колебаться на фундаменте на ± 1 мм в горизонтальном направлении. Если двигатель закрепить болтами на фундаменте, то такому перемещению будет препятствовать упругость грунта. Фундамент будет теперь составлять часть неподвижной массы, и если, скажем, он весит 12 000 кг, то полное перемещение двигателя (не будь упругого грунта) было бы уже не 2 мм, а только 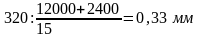(амплитуда колебаний вдали от резонанса, когда ω << ω_с, составит ± 0,17 мм).

Полученная система аналогична схеме, показанной на рис. 2.1, а; здесь масса А – двигатель с фундаментом, а роль пружины выполняет грунт; возбуждающей силой служит сила инерции поршня, которая с достаточной точностью выражается уравнением

, (2.31)

где m – масса поступательно движущихся частей; R – радиус кривошипа; α = ωt – угол поворота колена вала от начального положения (наружной мертвой точки); ω – угловая скорость вращения вала; 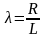– отношение радиуса кривошипа к длине шатуна.

Из уравнения (2.31) следует, что возбуждающая сила будет увеличиваться при изменении скорости вращения пропорционально ω². Такое возбуждение силами инерции, развивающимися при вращении двигателя, называют инерционным. Уравнение (2.31) можно переписать в следующем виде:

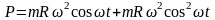. (2.32)

Можно, следовательно, считать, что инерционное возбуждение от перемещения поршня состоит из двух гармонических сил: первый член в правой части – гармоническая сила с частотой ω и ампли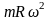тудой , второй – с частотой 2ω и амплитудой 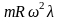(сила инерции первого порядка и сила инерции второго порядка). Так как , то сила инерции второго порядка в несколько раз меньше силы инерции первого порядка.

Приведенное выше вычисление колебания массы двигателя выполнено упрощенно, как бы для простого гармонического движения поршня (что верно для шатуна бесконечной длины).

Так как для неподвижности центра тяжести нужно, чтобы сила поршня уравновесила силу инерции двигателя, то , где ω – круговая частота колебаний, равная угловой скорости вращения вала. Отсюда амплитуда перемещений двигателя 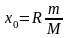, где М – масса двигателя. Следовательно, , как было найдено выше, когда мы не рассматривали силы инерции, а пользовались законом центра тяжести (центра инерции). Здесь речь шла о вынужденных колебаниях при отсутствии восстанавливающей силы. Система, показанная на рис. 2.14, не обладает собственной частотой и для нее резонанс невозможен. Однако, когда двигатель закреплен на фундаменте, появляется восстанавливающая сила (упругость грунта) и возникает опасность резонанса.

Если колено вала двигателя (рис. 2.14) не имеет противовеса, то при работе двигателя возникнет еще сила инерции 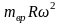, где m_вр – неуравновешенная вращающаяся масса, отнесенная к радиусу кривошипа. Точно так же такая сила возникнет и при вращении вала с диском (ротора), если центр тяжести диска не лежит на оси вращения (подобная конструкция показана на рис. 2.13, в). Такое инерционное возбуждение подробнее рассмотрено ниже.