2.3. Уравнения движения механической системы с одной степенью свободы.

Собственная частота колебаний

Пренебрегая пока массой пружины и полагая массу груза А равной m, можно написать:

.

Подставляя выражения W_р, W_к и W₀ в уравнение (2.1), получим

. (2.2)

Из уравнения (2.2) можно определить закон движения массы А, т.е. зависимость пути ее х от времени t:

или

. (2.3)

Положим ; тогда dx = x₀dy и, следовательно,

. (2.4)

Интегрируя выражение (4), получаем

. (2.5)

При y = 0, x = 0 постоянная интегрирования 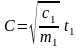, где t₁ – момент времени, когда масса А проходит через среднее положение О (т.е. x = 0). Подставляя размерности c и m, видим, что величина имеет размерность и, следовательно, есть некоторая угловая скорость; обозначим ее через ω и запишем равенство (2.5) в виде

или

,

откуда находим:

, (2.6)

где ω = , а ε = ωt₁ – некоторый угол в рад.

Угол ε, соответствующий времени t₁, определяется произвольным выбором начального момента t₁ = 0. Если начать рассматривать движение с момента прохода массы через нейтральное положение, то t₁ = 0 и ε = 0.

Таким образом, масса А на пружине, если эту массу вывести из положения покоя и отпустить, будет совершать гармонические колебания, т.е. график пути по времени представляет собой синусоиду.

Выведем формулу (2.6) ещё раз, пользуясь при составлении уравнения силами.

На массу А, оттянутую в крайнее положение, действует только одна сила – сила пружины Р. Будем считать положительным направление движения массы от среднего положения О, т.е. считать х положительным в направлении ОО₁ (см. рис. 2.1, а). Тогда восстанавливающая сила Р, как направленная от О₁ к О, должна считаться отрицательной. По второму закону Ньютона сила, вызывающая движение, измеряется произведением mx и, следовательно,

; (2.7)

отсюда

. (2.8)

Вместо уравнения (2.7) можно, пользуясь принципом Даламбера, написать, что сумма всех сил, действующих на тело, включая так называемую силу инерции, взятую с обратным знаком, равна нулю, т.е.

. (2.9)

откуда вытекает уравнение (2.8).

Принцип Даламбера позволяет формально заменять уравнение движения (2.7) уравнением (2.9), выражающим статическое уравнение сил, действующих на систему. В действительности сила - к движущей массе m не приложена. Такую силу испытывает действующая на массу m пружина (сила сопротивления). Равновесия приложенных к m сил не существует, поэтому масса и движется. Если бы мы стали рассматривать вместо участка пути ОО₁ участок ОО₂, то и на нем знаки перемещения от О к О₂ и восстанавливающей силы были бы противоположными и мы вновь пришли бы к уравнению (2.8). Иногда при выводе уравнения (2.8) говорят, что знак восстанавливающей силы отрицателен, так как она направлена в сторону, противоположную движению. Это выражение неясно, если не указать, что положительным направлением движения считается отклонение от среднего, нейтрального положения. В самом деле, при движении от О₁ к О направления действия восстанавливающей силы и движения совпадают. В рассматриваемом простом случае об этом не стоило бы упоминать, но, когда изучается более сложная система и всем действующим восстанавливающим силам приходится приписать знаки, легко сделать ошибку, если пользоваться неясной формулировкой.

Преобразуя уравнение (2.8), можно написать:

или

, (2.10)

где через ω по-прежнему обозначен .

Полное решение однородного линейного дифференциального уравнения (2.10) есть сумма двух частных решений. В качестве частных решений пробуем х₁ = С₁ sin ωt и х₂ = С₂ cos ωt. Действительно, после двукратного дифференцирования находим  = С₁ω cos ωt;  = С₁ω² sin ωt и, подставляя значение и х₁ в уравнение (2.10), получаем - С₁ω² sin ωt + ω² С₁ sin ωt = 0.

Точно так же удовлетворяет уравнению (2.10) и частное решение х₂ = С₂ cos ωt.

Следовательно,

.

Произвольные постоянные С₁ и С₂ должны быть определены из начальных условий. В качестве последних выбираем значения пути и скорости массы А, когда она находится в крайнем положении. Очевидно, пройденный путь в этот момент равен х₀, а скорость = 0.

Следовательно, в начальный момент t₀

;

. (2.11)

Из уравнений (2.11) находим

и .

Подставляя эти выражения для С₁ и С₂ в уравнение х = х₁ + х₂, получим

. (2.12)

При выводе формулы (2.6) было принято, что в момент t₁ масса А проходит через среднее положение. Так как через t₀ обозначен момент, когда масса находится в крайнем положении, то между t₁ и t₀ протекает четверть времени полного колебания, которому соответствует полная волна синусоиды, т.е. угол 2π. Следовательно,

. (2.13)

Если принять во внимание формулу (2.13), то выражение (2.12) дает следующее:

,

что совпадает с формулой (6).

Величину ω = называют круговой частотой свободных колебаний системы, или собственной круговой частотой. Отметим, что в выражение собственной круговой частоты ω не входит х₀, т.е. максимальное отклонение колеблющейся массы от среднего положения, называемое амплитудой колебания. Величина ω зависит только от характеристик силы, для рис. 2.1, а – от жесткости пружины и массы груза А и не зависит от амплитуды.

Совершенно так же, как для системы на рис. 2.1, а, выводят выражение собственной частоты крутильных колебаний системы рис. 1, б. Крутильной жесткостью с называют момент (н·м), закручивающий вал на 1 рад. Уравнение движения, аналогично уравнению (2.8), имеет следующий вид:

. (2.14)

Здесь вместо массы m вводится момент инерции диска J кг·м²; вместо линейного перемещения x – угол закрутки вала φ; вместо линейной жесткости с – крутильная. Решение уравнения (2.14) соответственно вместо выражения (2.6) записывается

, (2.15)

где ω = по-прежнему имеет размерность , так как с выражается в н·м, т.е. в кг·м²·сек^-2, а J – в кг·м².

Для системы на рис. 2.1, в, где прогиб – линейное перемещение, уравнение движения и решение его те же, что и для системы, изображенной на рис. 2.1, а (если стрелу прогиба обозначить через х). Изгибная жесткость балки или стержня зависит от типа опор (свободно опертый стержень, защемленный и т.д.) и может быть вычислена по величине прогиба f, приводимой в справочниках для различных случаев нагружения балок. Так как изгибная жесткость , то, например, из выражения прогиба для случая, показанного на рис. 2.1, в, где , находим:

,

где l – длина балки, м; J – момент инерции сечения, м⁴; E – модуль упругости, н/м².

Отклонения различных сечений вала, показанного на рис. 2.1, в, от среднего положения при максимальном прогибе, т.е. упругая линия вала дает форму колебаний системы. Аналогично график на рис. 2.1, а, на котором амплитуды точек пружины отложены на перпендикулярах к отрезку, изображающему длину пружины, или график на рис. 2.1, б, где также отложены амплитуды углов закрутки вала, называют формами колебаний системы с, m или соответственно системы c, J.