ФГБОУ ВПО «Воронежский государственный технический университет»

Г.В. Янов А.И. Барсукова Т.Л. Тураева

А.А. Долгачев

МЕХАНИКА

Утверждено Редакционно-издательским советом

университета в качестве учебного пособия

Воронеж 2012

УДК 681.3; 53

Механика: учеб. пособие / Г.В. Янов, А.И. Барсукова, Т.Л. Тураева, А.А. Долгачев. Воронеж: ФГБОУ ВПО «Воронежский государственный технический университет», 2012. 119 с.

Учебное пособие позволяет организовать самостоятельную работу студентов, содержит вариативные задания, а также уровневые тестовые задания для самостоятельных и контрольных работ по разделам механики и предназначено для преподавателей, студентов втузов всех направлений подготовки и специальностей.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по направлениям подготовки, реализуемым в ФГБОУ ВПО «Воронежский государственный технический университет», дисциплине «Физика».

Учебное пособие подготовлено в электронном виде в текстовом редакторе MS WORD XP и содержится в файле «Механика.doc».

Табл. 5. Ил. 55. Библиогр.: 10 назв.

Рецензенты: кафедра теоретической физики Воронежского государственного университета (канд. физ.-мат. наук, доц. А.Н. Алмалиев;

д-р физ.-мат. наук, проф. С.А. Антипов

© Янов Г.В., Барсукова А.И., Тураева Т.Л., Долгачев А.А., 2012

© Оформление. ФГБОУ ВПО «Воронежский государственный технический университет», 2012

Предисловие

В учебном пособии систематически кратко изложен материал, а также представлен перечень основных законов и формул по различным темам из раздела механика. Рассмотрены 19 заданий в 20 вариантах, даны образцы решения базовых задач, тестовые задания открытого и закрытого типа для выявления оценки знаний всех уровней. Содержание задач, их типы, степень сложности и способы решения различны. Это позволяет использовать их для групповой и индивидуальной работы со студентами, а также организации самостоятельной работы студентов и составлении контрольных работ. Большинство задач составлено авторами, часть заимствована из известных пособий, но переработана. Названия и обозначения единиц измерения величин, используемых в пособии, соответствуют Международной системе единиц измерения (СИ).

1. Элементы векторного анализа

В курсе общей физики приходится оперировать скалярными (скаляр) и векторными (вектор) величинами. Скаляром называется величина, характеризующаяся только числовым значением. Векторы на рисунках изображаются в виде прямолинейных отрезков со стрелкой на конце, которые характеризуются числовым значением (длиной или модулем вектора - положительным скаляром), направлением и точкой приложения. В тексте векторы принято обозначать жирными буквами или над буквами ставить стрелку, а просто та же буква означает модуль вектора. Действия над векторами подчиняются определенным закономерностям.

Сложение и вычитание векторов. Векторы могут быть отложены из любой точки пространства. Возможен перенос вектора параллельно себе без изменения его направления. Суммой векторов a, b и с (составляющих векторов) называется вектор

d = a + b + c (результирующий вектор), который соединяет начало первого вектора с концом последнего вектора в ломаной линии из составляющих векторов, которые располагаются таким образом, что к концу предыдущего составляющего вектора пристраивается последующий в любом порядке (правило многоугольника, рис.1). Разностью векторов а и b называется такой вектор с = a - b = a + ( - b), который в сумме с вектором b дает вектор а = b + c (рис.2).

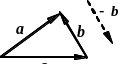
Рис.1 Рис. 2

Умножение вектора на скаляр. Умножение вектора а на положительный скаляр n > 0 дает вектор b = n · а того же направления, что и вектор а, но в n раз больше по величине (рис.3). Умножение вектора а на отрицательный скаляр -m < 0 дает вектор d= -m · а противоположного вектору а направления и в | - m | раз больший по величине (рис.4). О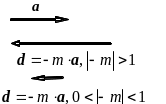 перации деления вектора на вектор не существует.

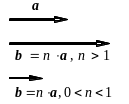
Рис. 3 Рис. 4

Скалярное произведение векторов. Скалярным произведением векторов а и b называется скаляр (а, b) = а· b cos α, равный произведению модулей этих векторов на косинус угла α между ними (рис.5). Скалярное произведение не зависит от порядка сомножителей:

(а, b) = (b, а).

Р ис. 5

Векторное произведение. Векторным произведением векторов а и b называется вектор с = [а, b] = a b sin α · n, равный по величине произведению модулей этих векторов на синус угла α между ними и совпадающий по направлению с нормальным единичным вектором n к плоскости, в которой лежат векторы а и b. Направление вектора с определяется по правилу правого винта, а векторы a, b и n образуют правовинтовую систему (рис.6). Перестановка сомножителей вызывает изменение направления результирующего вектора на противоположное, так как векторное произведение определяется направлением вращения от первого сомножителя ко второму:

[а, b] = - [b, а].

В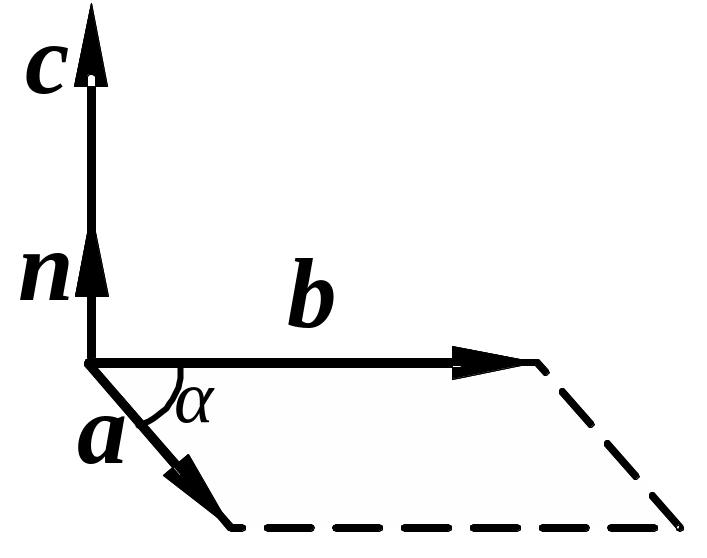 екторы типа [а, b], направление которых связывается с направлением вращения, называются псевдовекторами (или аксиальными векторами). При изменении условия, например, при переходе от правой системы координат к левой, направления псевдовекторов изменяются на обратные, истинные же векторы при этом остаются без изменений. Векторное произведение будет псевдовектором, когда оба перемножаемых вектора являются истинными (или оба – псевдовекторы). Векторное произведение истинного вектора на псевдовектор будет истинным вектором.

Рис. 6

Скалярно-векторное произведение. Скалярно-векторным произведением трех векторов называется выражение (а, [b, c]) = а (b · c sin α) cos β, равное скалярному произведению вектора а на векторное произведение векторов b и c, где α - угол между векторами b и c, β - угол между вектором а и нормальным единичным вектором n, определяющим направление вектора [b, c]. Допускается циклическая перестановка сомножителей откуда следует, что (а, [b, c]) = (b, [c, а]) = (c, [а, b]).

Двойное векторное произведение. Двойным векторным произведением трех векторов a, b и c называется вектор d = [a, [b, c]] перпендикулярный обоим сомножителям, поэтому вектор d перпендикулярен к нормальному единичному вектору n, определяющему направление вектора [b, c]. Вектор d можно определить исходя из следующего соотношения:

[a, [b, c]] = b (a, c) - c (a, b).

Радиус-вектор. Радиусом-вектором некоторой точки М (x, y, z) пространства называется вектор, проведенный из начала координатной системы О в данную точку М (рис.7). Как и любой вектор, радиус-вектор можно выразить через его проекции на оси координат , , и единичные векторы (орты) этих осей i, j, и k, соответственно, в виде линейного выражения:

= = x · i + y · j + z · k,

где проекции на координатные оси можно приравнять декартовым координатам данной точки:

Длина радиус-вектора в этом случае определяется из соотношения:

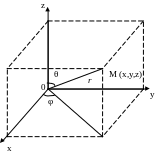
Рис. 7

Производная функции. Дифференциалом (приращением) функции ƒ(t) называется выражение:

d ƒ = ƒ′ · d t,

где ƒ′ - производная ƒ по t. Приращение функции за очень малый, но конечный промежуток времени Δ t приближенно равно:

Δ ƒ  ƒ′ · Δ t = Δ t.

Аналогичную формулу можно написать и для любого вектора, который изменяется со временем по известному закону a (t):

.

Производная скалярного произведения двух векторов a(t) и b(t) вычисляется по формуле:

Производная векторного произведения векторов a(t) и b(t) вычисляется по формуле:

Рассмотрим примеры решения задач на действия с векторными величинами.

Пример 1. Радиус-вектор частицы изменяется со временем по закону:

r = 5t · i + 4t · j + 3 · k (м).

Найдите скорость v и ускорение а частицы и их абсолютные значения.

Решение: Скорость равна первой производной радиуса-вектора по времени, откуда:

v = = 10t · i + 4 · j (м/c).

м/c

Ускорение равно первой производной вектора скорости или второй производной радиуса-вектора по времени:

a = = = 10 · i (м/с ).

a=10 м/с

Пример 2. Частица движется со скоростью v = 3 · i + 4t · j + 9t · k (м/с). Найдите перемещение r частицы за первые 3 секунды ее движения и его модуль.

Решение: Интегрированием находим изменение со временем радиуса-вектора частицы r:

Δr = = 3t · i + 2t · j + 3t · k | = 9 i + 18 j + 81 k .

Δr = м

Таблица 1

Производные основных элементарных функций

с	0	ln(x)	1/x
x	1	sin(x)	cos(x)
xn	nxn-1	cos(x)	-sin(x)
ex	ex	tg(x)	1/cos2(x)
ax	axln(a)	ctg(x)	-1/sin2(x)

Таблица 2